Question Number 72194 by mr W last updated on 26/Oct/19
Commented by mr W last updated on 26/Oct/19
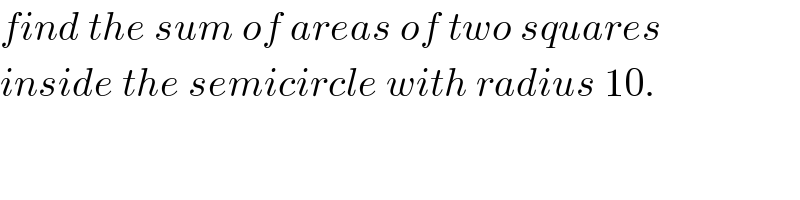
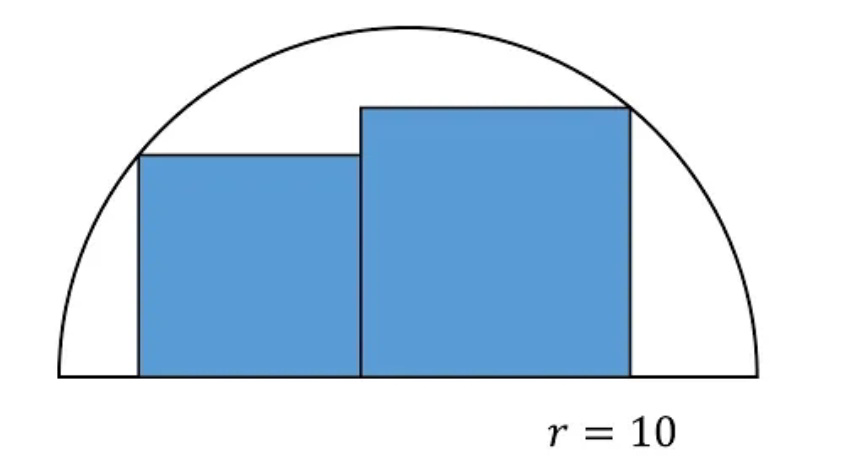
$${find}\:{the}\:{sum}\:{of}\:{areas}\:{of}\:{two}\:{squares} \\ $$$${inside}\:{the}\:{semicircle}\:{with}\:{radius}\:\mathrm{10}. \\ $$
Answered by MJS last updated on 27/Oct/19

$$\mathrm{I}\:\mathrm{turned}\:\mathrm{it}\:\mathrm{around} \\ $$$$\mathrm{if}\:\mathrm{the}\:\mathrm{larger}\:\mathrm{square}\:\mathrm{has}\:\mathrm{side}\:\mathrm{length}\:\mathrm{1},\:\mathrm{which} \\ $$$$\mathrm{side}\:\mathrm{lengths}\:\mathrm{are}\:\mathrm{possible}\:\mathrm{for}\:\mathrm{the}\:\mathrm{smaller}\:\mathrm{square}? \\ $$$$\mathrm{put}\:\mathrm{the}\:\mathrm{right}\:\mathrm{upper}\:\mathrm{vertice}\:\begin{pmatrix}{\mathrm{1}}\\{\mathrm{1}}\end{pmatrix},\:\mathrm{the}\:\mathrm{left}\:\mathrm{upper} \\ $$$$\mathrm{one}\:\begin{pmatrix}{−{s}}\\{{s}}\end{pmatrix} \\ $$$$\mathrm{both}\:\mathrm{must}\:\mathrm{be}\:\mathrm{on}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{center}\:\mathrm{on}\:\mathrm{the} \\ $$$${x}−\mathrm{axis} \\ $$$$\left({x}−{p}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$$\mathrm{upper}\:\mathrm{semi}\:\mathrm{circle}:\:{y}=\sqrt{\mathrm{2}{s}−\mathrm{2}\left({s}−\mathrm{1}\right){x}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{the}\:\mathrm{upper}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{the}\:\mathrm{larger}\:\mathrm{square}\:\mathrm{must} \\ $$$$\mathrm{fit}\:\mathrm{into}\:\mathrm{the}\:\mathrm{circle}\:\Rightarrow\:{y}\geqslant\mathrm{1}\:\mathrm{at}\:{x}=\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\leqslant{s}<\mathrm{1} \\ $$$$\mathrm{now}\:\mathrm{choose}\:{s} \\ $$$$\Rightarrow\:\mathrm{area}={s}^{\mathrm{2}} +\mathrm{1};\:{r}=\sqrt{{s}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{area}\:\mathrm{within}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{radius}\:\mathrm{10}\:\mathrm{is} \\ $$$$\frac{{s}^{\mathrm{2}} +\mathrm{1}}{\left(\sqrt{{s}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }×\mathrm{100}=\mathrm{100} \\ $$
Commented by mr W last updated on 27/Oct/19

$${thanks}\:{sir}! \\ $$
Answered by mr W last updated on 27/Oct/19
Commented by mr W last updated on 27/Oct/19
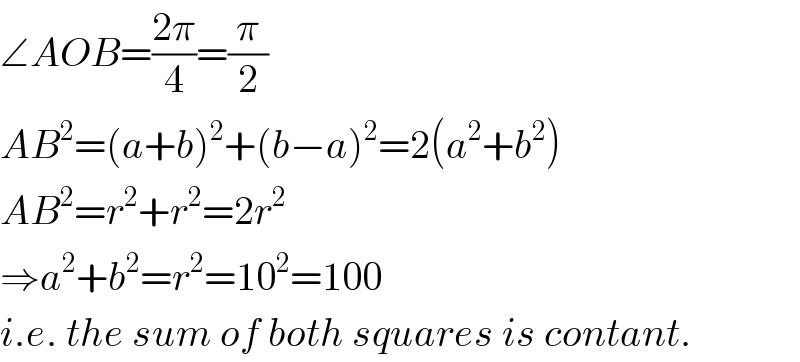
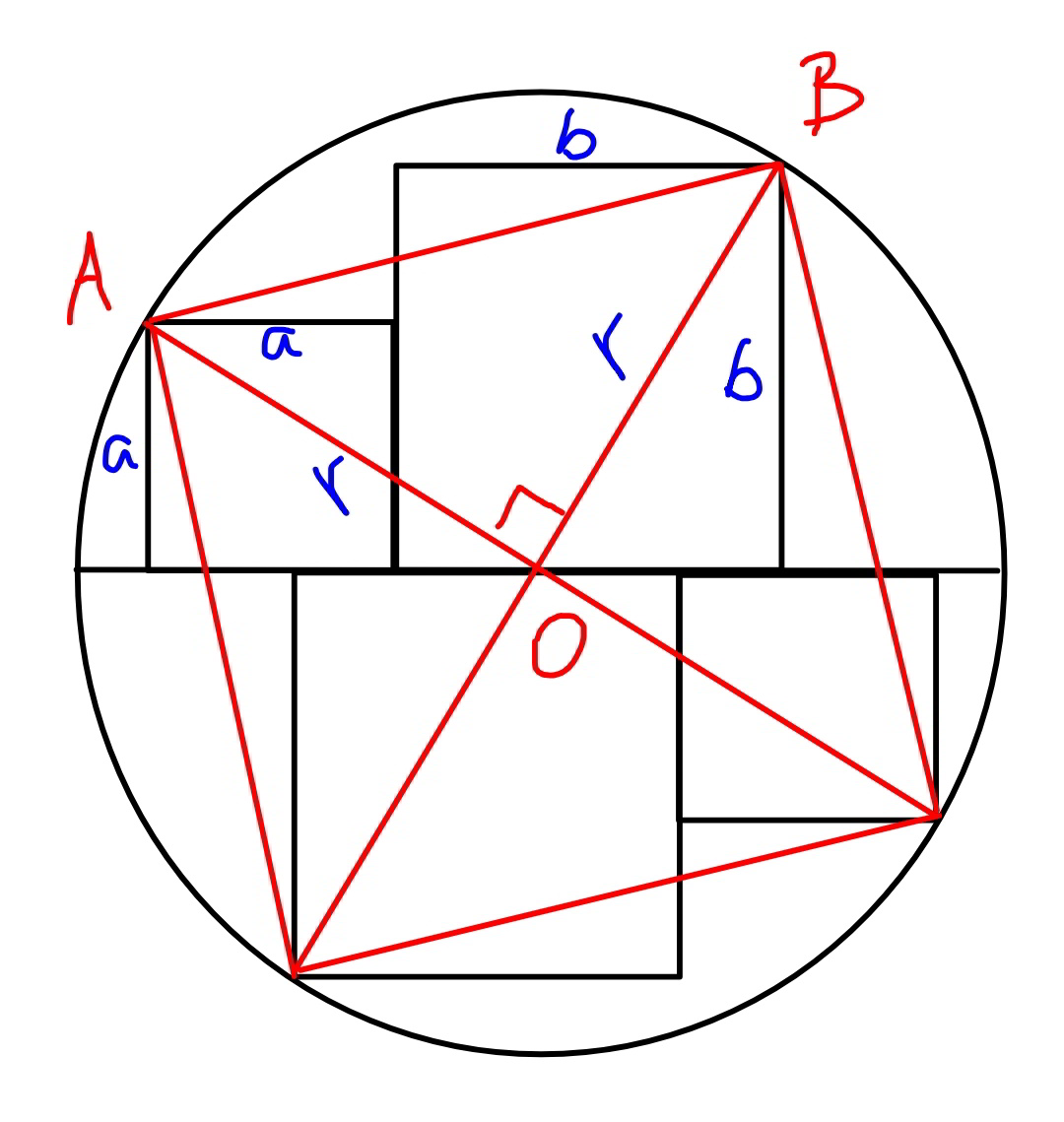
$$\angle{AOB}=\frac{\mathrm{2}\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{2}} \\ $$$${AB}^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} +\left({b}−{a}\right)^{\mathrm{2}} =\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$${AB}^{\mathrm{2}} ={r}^{\mathrm{2}} +{r}^{\mathrm{2}} =\mathrm{2}{r}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={r}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} =\mathrm{100} \\ $$$${i}.{e}.\:{the}\:{sum}\:{of}\:{both}\:{squares}\:{is}\:{contant}. \\ $$
Commented by ajfour last updated on 27/Oct/19
$${Great}\:{way}\:{Sir},\:{i}\:{myself}\:{had} \\ $$$${thought}\:{to}\:{attempt}\:{it}\:{somewhat} \\ $$$${this}\:{way}.. \\ $$
