Menu Close

Question-72198

Tinku Tara 0 Comments
Pin




Question Number 72198 by mr W last updated on 26/Oct/19
Commented by mr W last updated on 26/Oct/19
the small ball with mass m and radius r is released at the given position. find the period of the swing motion. pure rolling is assumed.
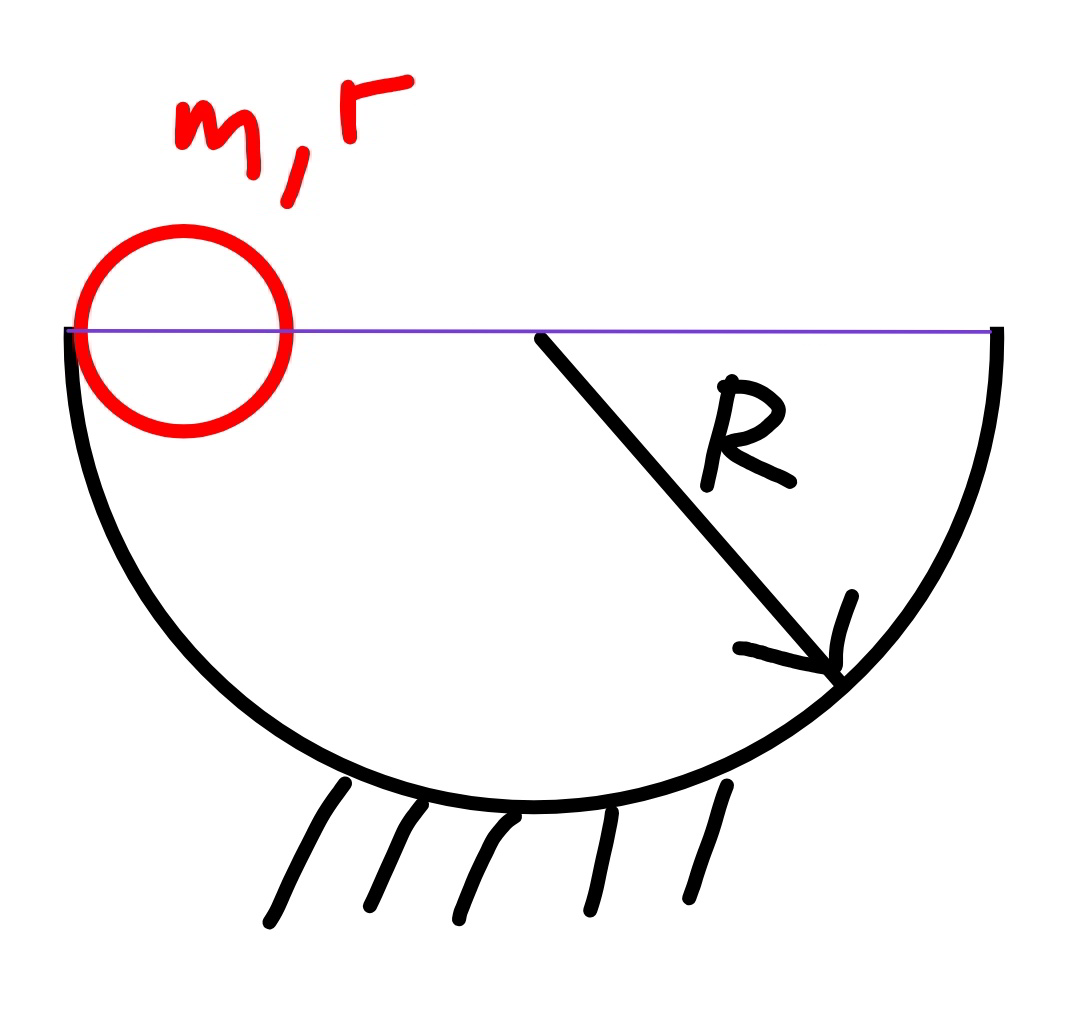
$${the}\:{small}\:{ball}\:{with}\:{mass}\:{m}\:{and}\:{radius} \\ $$$${r}\:{is}\:{released}\:{at}\:{the}\:{given}\:{position}. \\ $$$${find}\:{the}\:{period}\:{of}\:{the}\:{swing}\:{motion}. \\ $$$${pure}\:{rolling}\:{is}\:{assumed}. \\ $$
Commented by ajfour last updated on 26/Oct/19
Commented by ajfour last updated on 26/Oct/19
Ω=(dθ/dt) fr=Iα , αr=(dv/dt) , v=(R−r)Ω mgcos θ−f=m(dv/dt) ⇒ mgcos θ−((Iαr)/r^2 )=mαr ⇒ gcos θ=(7/5)(R−r)Ω((dΩ/dθ)) ⇒ Ω^2 =((10g)/(7(R−r)))sin θ ⇒ ∫_0 ^( π) (dθ/( (√(sin θ))))=((√((10g)/(7(R−r)))))(T/2) ⇒ T = (√((28(R−r))/(10g)))∫_0 ^( π) (dθ/( (√(sin θ)))) . ϕ= ((Rθ)/r)−θ (dϕ/dt)=(((R−r))/r)(dθ/dt) = (((R−r))/r)Ω ⇒ ωr=v=(R−r)Ω
$$\:\:\Omega=\frac{{d}\theta}{{dt}} \\ $$$${fr}={I}\alpha\:\:,\:\alpha{r}=\frac{{dv}}{{dt}}\:\:,\:\:{v}=\left({R}−{r}\right)\Omega \\ $$$${mg}\mathrm{cos}\:\theta−{f}={m}\frac{{dv}}{{dt}} \\ $$$$\Rightarrow\:\:{mg}\mathrm{cos}\:\theta−\frac{{I}\alpha{r}}{{r}^{\mathrm{2}} }={m}\alpha{r} \\ $$$$\Rightarrow\:\:{g}\mathrm{cos}\:\theta=\frac{\mathrm{7}}{\mathrm{5}}\left({R}−{r}\right)\Omega\left(\frac{{d}\Omega}{{d}\theta}\right) \\ $$$$\Rightarrow\:\:\Omega^{\mathrm{2}} =\frac{\mathrm{10}{g}}{\mathrm{7}\left({R}−{r}\right)}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\:\int_{\mathrm{0}} ^{\:\pi} \frac{{d}\theta}{\:\sqrt{\mathrm{sin}\:\theta}}=\left(\sqrt{\frac{\mathrm{10}{g}}{\mathrm{7}\left({R}−{r}\right)}}\right)\frac{{T}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:{T}\:=\:\sqrt{\frac{\mathrm{28}\left({R}−{r}\right)}{\mathrm{10}{g}}}\int_{\mathrm{0}} ^{\:\pi} \frac{{d}\theta}{\:\sqrt{\mathrm{sin}\:\theta}}\:\:. \\ $$$$\:\:\:\varphi=\:\frac{{R}\theta}{{r}}−\theta \\ $$$$\:\frac{{d}\varphi}{{dt}}=\frac{\left({R}−{r}\right)}{{r}}\frac{{d}\theta}{{dt}}\:=\:\frac{\left({R}−{r}\right)}{{r}}\Omega \\ $$$$\Rightarrow\:\:\omega{r}={v}=\left({R}−{r}\right)\Omega \\ $$
Commented by ajfour last updated on 26/Oct/19
Commented by ajfour last updated on 26/Oct/19
For the round trip θ=2π ϕ=((2πR)/r)−2π
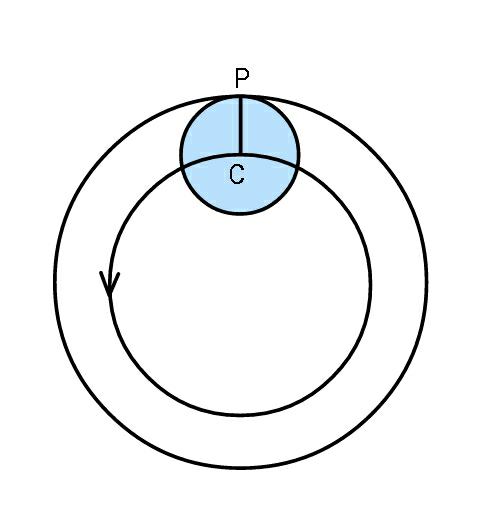
$${For}\:{the}\:{round}\:{trip}\:\theta=\mathrm{2}\pi \\ $$$$\:\:\varphi=\frac{\mathrm{2}\pi{R}}{{r}}−\mathrm{2}\pi \\ $$
Commented by ajfour last updated on 26/Oct/19
Commented by ajfour last updated on 26/Oct/19
ϕ=((Rθ)/r)−θ =(((R−r)θ)/r) (dϕ/dt)=(((R−r))/r)(dθ/dt) or dϕ=((Rdθ)/r)−dθ
$$\varphi=\frac{{R}\theta}{{r}}−\theta\:=\frac{\left({R}−{r}\right)\theta}{{r}} \\ $$$$\frac{{d}\varphi}{{dt}}=\frac{\left({R}−{r}\right)}{{r}}\frac{{d}\theta}{{dt}} \\ $$$${or}\:\:\:\:{d}\varphi=\frac{{Rd}\theta}{{r}}−{d}\theta \\ $$
Commented by mr W last updated on 26/Oct/19
thanks alot for the nice explanation! now i see where the problem is.
$${thanks}\:{alot}\:{for}\:{the}\:{nice}\:{explanation}! \\ $$$${now}\:{i}\:{see}\:{where}\:{the}\:{problem}\:{is}. \\ $$
Answered by mr W last updated on 26/Oct/19
Commented by mr W last updated on 26/Oct/19
ϕ=((R−r)/r)θ ω=(dϕ/dt)=((R−r)/r)×(dθ/dt)=((R−r)/r)Ω with Ω=(dθ/dt) α=(dω/dt)=((R−r)/r)×(dΩ/dθ)=((R−r)/r)×Ω(dΩ/dθ) I_P =I_C +mr^2 =((2mr^2 )/5)+mr^2 =((7mr^2 )/5) I_P α=mgr cos θ ((7mr^2 )/5)×((R−r)/r)Ω(dΩ/dθ)=mgr cos θ ΩdΩ=((5g)/(7R)) cos θ dθ ∫_0 ^Ω ΩdΩ=((5g)/(7(R−r))) ∫_0 ^θ cos θ dθ (Ω^2 /2)=((5g)/(7(R−r))) sin θ ⇒Ω=(dθ/dt)=(√((10g)/(7(R−r))))(√(sin θ)) ⇒dt=(√((7(R−r))/(10g)))×(dθ/( (√(sin θ)))) ⇒t=(√((7(R−r))/(10g)))×∫_0 ^θ (dθ/( (√(sin θ)))) ⇒T=4×(√((7(R−r))/(10g)))×∫_0 ^(π/2) (dθ/( (√(sin θ)))) ∫_0 ^(π/2) (dθ/( (√(sin θ))))≈2.6221 ⇒T≈4×(√((7(R−r))/(10g)))×2.6221=8.775(√((R−r)/g))
$$\varphi=\frac{{R}−{r}}{{r}}\theta \\ $$$$\omega=\frac{{d}\varphi}{{dt}}=\frac{{R}−{r}}{{r}}×\frac{{d}\theta}{{dt}}=\frac{{R}−{r}}{{r}}\Omega\:{with}\:\Omega=\frac{{d}\theta}{{dt}} \\ $$$$\alpha=\frac{{d}\omega}{{dt}}=\frac{{R}−{r}}{{r}}×\frac{{d}\Omega}{{d}\theta}=\frac{{R}−{r}}{{r}}×\Omega\frac{{d}\Omega}{{d}\theta} \\ $$$${I}_{{P}} ={I}_{{C}} +{mr}^{\mathrm{2}} =\frac{\mathrm{2}{mr}^{\mathrm{2}} }{\mathrm{5}}+{mr}^{\mathrm{2}} =\frac{\mathrm{7}{mr}^{\mathrm{2}} }{\mathrm{5}} \\ $$$${I}_{{P}} \alpha={mgr}\:\mathrm{cos}\:\theta \\ $$$$\frac{\mathrm{7}{mr}^{\mathrm{2}} }{\mathrm{5}}×\frac{{R}−{r}}{{r}}\Omega\frac{{d}\Omega}{{d}\theta}={mgr}\:\mathrm{cos}\:\theta \\ $$$$\Omega{d}\Omega=\frac{\mathrm{5}{g}}{\mathrm{7}{R}}\:\mathrm{cos}\:\theta\:{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\Omega} \Omega{d}\Omega=\frac{\mathrm{5}{g}}{\mathrm{7}\left({R}−{r}\right)}\:\int_{\mathrm{0}} ^{\theta} \mathrm{cos}\:\theta\:{d}\theta \\ $$$$\frac{\Omega^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{5}{g}}{\mathrm{7}\left({R}−{r}\right)}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\Omega=\frac{{d}\theta}{{dt}}=\sqrt{\frac{\mathrm{10}{g}}{\mathrm{7}\left({R}−{r}\right)}}\sqrt{\mathrm{sin}\:\theta} \\ $$$$\Rightarrow{dt}=\sqrt{\frac{\mathrm{7}\left({R}−{r}\right)}{\mathrm{10}{g}}}×\frac{{d}\theta}{\:\sqrt{\mathrm{sin}\:\theta}} \\ $$$$\Rightarrow{t}=\sqrt{\frac{\mathrm{7}\left({R}−{r}\right)}{\mathrm{10}{g}}}×\int_{\mathrm{0}} ^{\theta} \frac{{d}\theta}{\:\sqrt{\mathrm{sin}\:\theta}} \\ $$$$\Rightarrow{T}=\mathrm{4}×\sqrt{\frac{\mathrm{7}\left({R}−{r}\right)}{\mathrm{10}{g}}}×\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\theta}{\:\sqrt{\mathrm{sin}\:\theta}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\theta}{\:\sqrt{\mathrm{sin}\:\theta}}\approx\mathrm{2}.\mathrm{6221} \\ $$$$\Rightarrow{T}\approx\mathrm{4}×\sqrt{\frac{\mathrm{7}\left({R}−{r}\right)}{\mathrm{10}{g}}}×\mathrm{2}.\mathrm{6221}=\mathrm{8}.\mathrm{775}\sqrt{\frac{{R}−{r}}{{g}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *