Question Number 72291 by aliesam last updated on 27/Oct/19
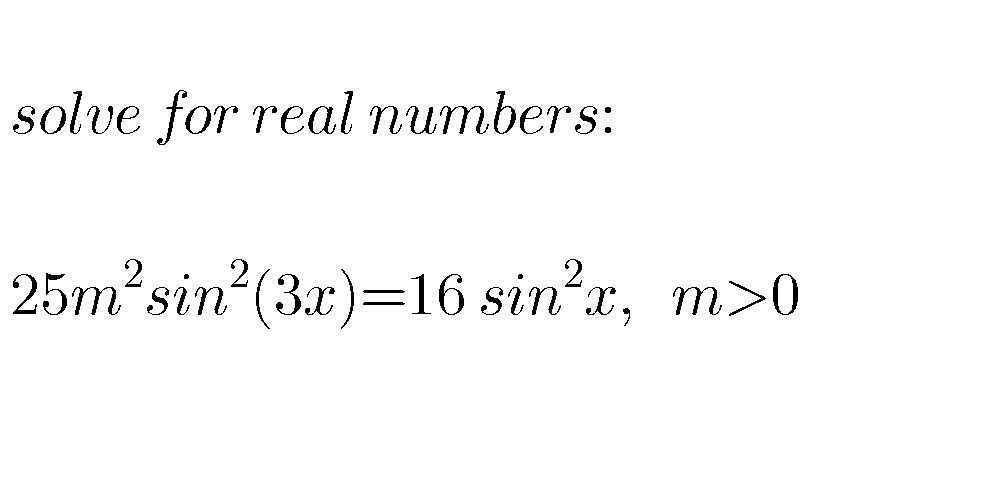
Answered by mr W last updated on 27/Oct/19
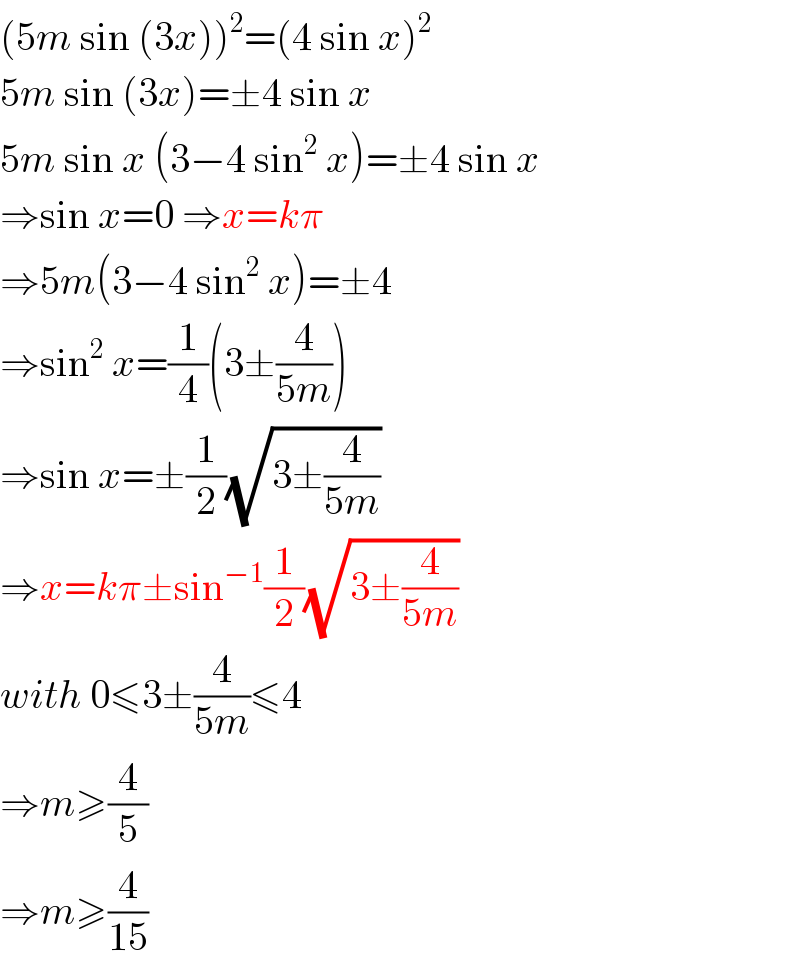
$$\left(\mathrm{5}{m}\:\mathrm{sin}\:\left(\mathrm{3}{x}\right)\right)^{\mathrm{2}} =\left(\mathrm{4}\:\mathrm{sin}\:{x}\right)^{\mathrm{2}} \\ $$$$\mathrm{5}{m}\:\mathrm{sin}\:\left(\mathrm{3}{x}\right)=\pm\mathrm{4}\:\mathrm{sin}\:{x} \\ $$$$\mathrm{5}{m}\:\mathrm{sin}\:{x}\:\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)=\pm\mathrm{4}\:\mathrm{sin}\:{x} \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\mathrm{0}\:\Rightarrow{x}={k}\pi \\ $$$$\Rightarrow\mathrm{5}{m}\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right)=\pm\mathrm{4} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \:{x}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}\pm\frac{\mathrm{4}}{\mathrm{5}{m}}\right) \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}\pm\frac{\mathrm{4}}{\mathrm{5}{m}}} \\ $$$$\Rightarrow{x}={k}\pi\pm\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}\pm\frac{\mathrm{4}}{\mathrm{5}{m}}} \\ $$$${with}\:\mathrm{0}\leqslant\mathrm{3}\pm\frac{\mathrm{4}}{\mathrm{5}{m}}\leqslant\mathrm{4} \\ $$$$\Rightarrow{m}\geqslant\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow{m}\geqslant\frac{\mathrm{4}}{\mathrm{15}} \\ $$
