Question-72434

Question Number 72434 by aliesam last updated on 28/Oct/19

Answered by mind is power last updated on 28/Oct/19

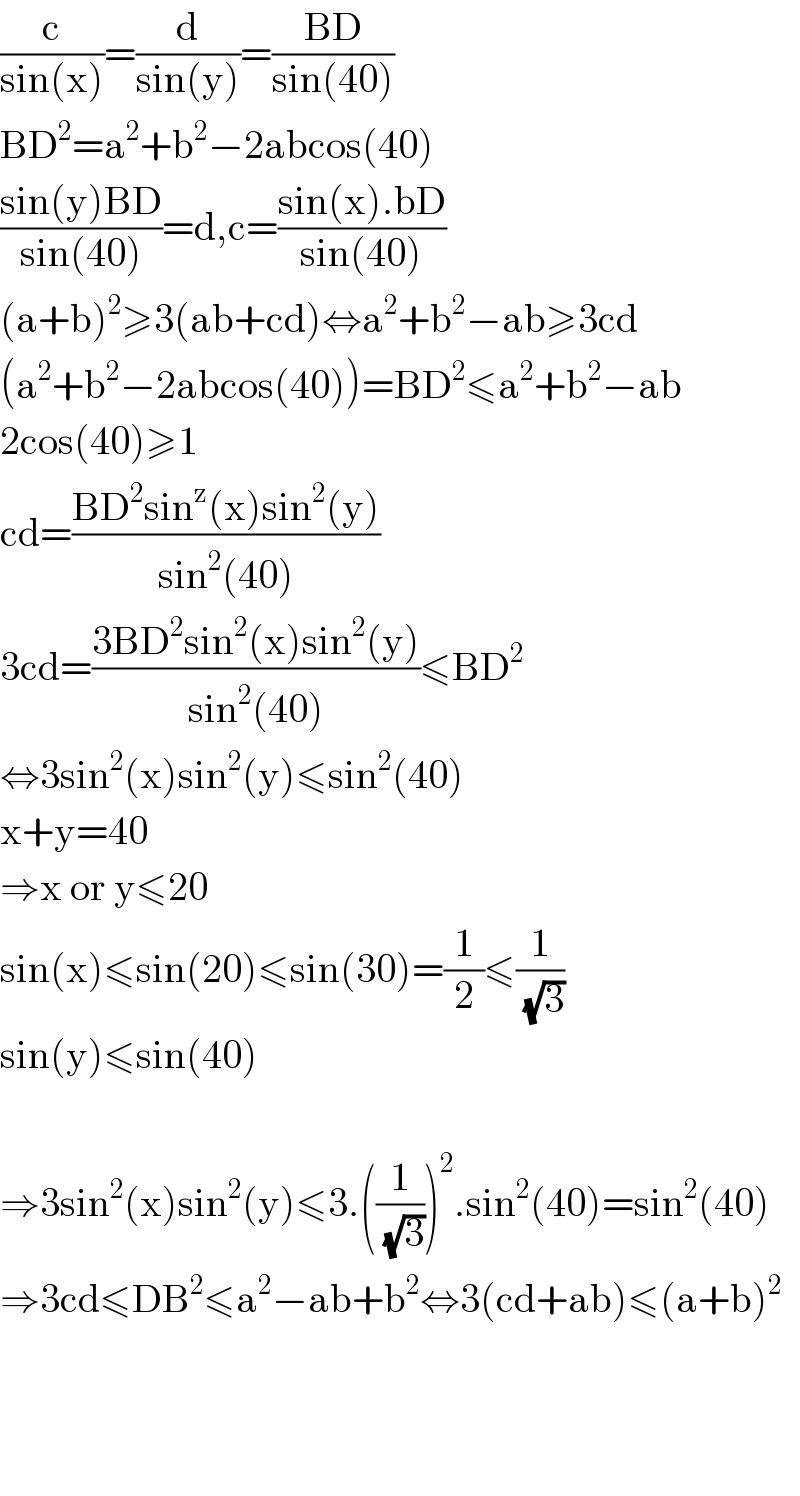
(c/(sin(x)))=(d/(sin(y)))=((BD)/(sin(40))) BD^2 =a^2 +b^2 −2abcos(40) ((sin(y)BD)/(sin(40)))=d,c=((sin(x).bD)/(sin(40))) (a+b)^2 ≥3(ab+cd)⇔a^2 +b^2 −ab≥3cd (a^2 +b^2 −2abcos(40))=BD^2 ≤a^2 +b^2 −ab 2cos(40)≥1 cd=((BD^2 sin^z (x)sin^2 (y))/(sin^2 (40))) 3cd=((3BD^2 sin^2 (x)sin^2 (y))/(sin^2 (40)))≤BD^2 ⇔3sin^2 (x)sin^2 (y)≤sin^2 (40) x+y=40 ⇒x or y≤20 sin(x)≤sin(20)≤sin(30)=(1/2)≤(1/( (√3))) sin(y)≤sin(40) ⇒3sin^2 (x)sin^2 (y)≤3.((1/( (√3))))^2 .sin^2 (40)=sin^2 (40) ⇒3cd≤DB^2 ≤a^2 −ab+b^2 ⇔3(cd+ab)≤(a+b)^2

$$\frac{\mathrm{c}}{\mathrm{sin}\left(\mathrm{x}\right)}=\frac{\mathrm{d}}{\mathrm{sin}\left(\mathrm{y}\right)}=\frac{\mathrm{BD}}{\mathrm{sin}\left(\mathrm{40}\right)} \\ $$$$\mathrm{BD}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2abcos}\left(\mathrm{40}\right) \\ $$$$\frac{\mathrm{sin}\left(\mathrm{y}\right)\mathrm{BD}}{\mathrm{sin}\left(\mathrm{40}\right)}=\mathrm{d},\mathrm{c}=\frac{\mathrm{sin}\left(\mathrm{x}\right).\mathrm{bD}}{\mathrm{sin}\left(\mathrm{40}\right)} \\ $$$$\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} \geqslant\mathrm{3}\left(\mathrm{ab}+\mathrm{cd}\right)\Leftrightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{ab}\geqslant\mathrm{3cd} \\ $$$$\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2abcos}\left(\mathrm{40}\right)\right)=\mathrm{BD}^{\mathrm{2}} \leqslant\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{ab} \\ $$$$\mathrm{2cos}\left(\mathrm{40}\right)\geqslant\mathrm{1} \\ $$$$\mathrm{cd}=\frac{\mathrm{BD}^{\mathrm{2}} \mathrm{sin}^{\mathrm{z}} \left(\mathrm{x}\right)\mathrm{sin}^{\mathrm{2}} \left(\mathrm{y}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{40}\right)} \\ $$$$\mathrm{3cd}=\frac{\mathrm{3BD}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{sin}^{\mathrm{2}} \left(\mathrm{y}\right)}{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{40}\right)}\leqslant\mathrm{BD}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{3sin}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{sin}^{\mathrm{2}} \left(\mathrm{y}\right)\leqslant\mathrm{sin}^{\mathrm{2}} \left(\mathrm{40}\right) \\ $$$$\mathrm{x}+\mathrm{y}=\mathrm{40} \\ $$$$\Rightarrow\mathrm{x}\:\mathrm{or}\:\mathrm{y}\leqslant\mathrm{20} \\ $$$$\mathrm{sin}\left(\mathrm{x}\right)\leqslant\mathrm{sin}\left(\mathrm{20}\right)\leqslant\mathrm{sin}\left(\mathrm{30}\right)=\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{sin}\left(\mathrm{y}\right)\leqslant\mathrm{sin}\left(\mathrm{40}\right) \\ $$$$ \\ $$$$\Rightarrow\mathrm{3sin}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{sin}^{\mathrm{2}} \left(\mathrm{y}\right)\leqslant\mathrm{3}.\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} .\mathrm{sin}^{\mathrm{2}} \left(\mathrm{40}\right)=\mathrm{sin}^{\mathrm{2}} \left(\mathrm{40}\right) \\ $$$$\Rightarrow\mathrm{3cd}\leqslant\mathrm{DB}^{\mathrm{2}} \leqslant\mathrm{a}^{\mathrm{2}} −\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \Leftrightarrow\mathrm{3}\left(\mathrm{cd}+\mathrm{ab}\right)\leqslant\left(\mathrm{a}+\mathrm{b}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by aliesam last updated on 28/Oct/19

$${god}\:{bless}\:{you}\:{sir}.\:{nice}\:{solution} \\ $$

Commented by mind is power last updated on 28/Oct/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply