Menu Close

Question-72519

Tinku Tara 0 Comments
Pin




Question Number 72519 by ajfour last updated on 29/Oct/19
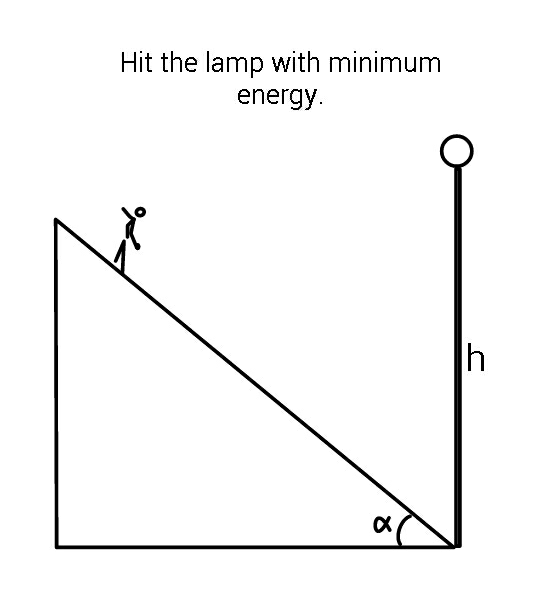
Commented by ajfour last updated on 29/Oct/19
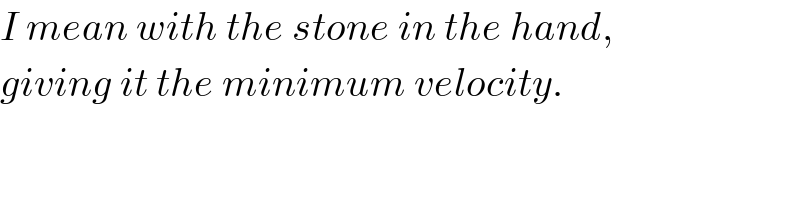
I mean with the stone in the hand, giving it the minimum velocity.
$${I}\:{mean}\:{with}\:{the}\:{stone}\:{in}\:{the}\:{hand}, \\ $$$${giving}\:{it}\:{the}\:{minimum}\:{velocity}. \\ $$
Answered by mr W last updated on 29/Oct/19
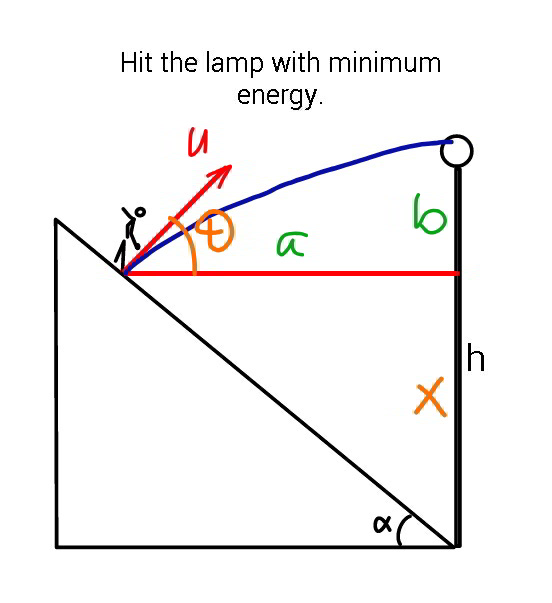
Commented by ajfour last updated on 30/Oct/19
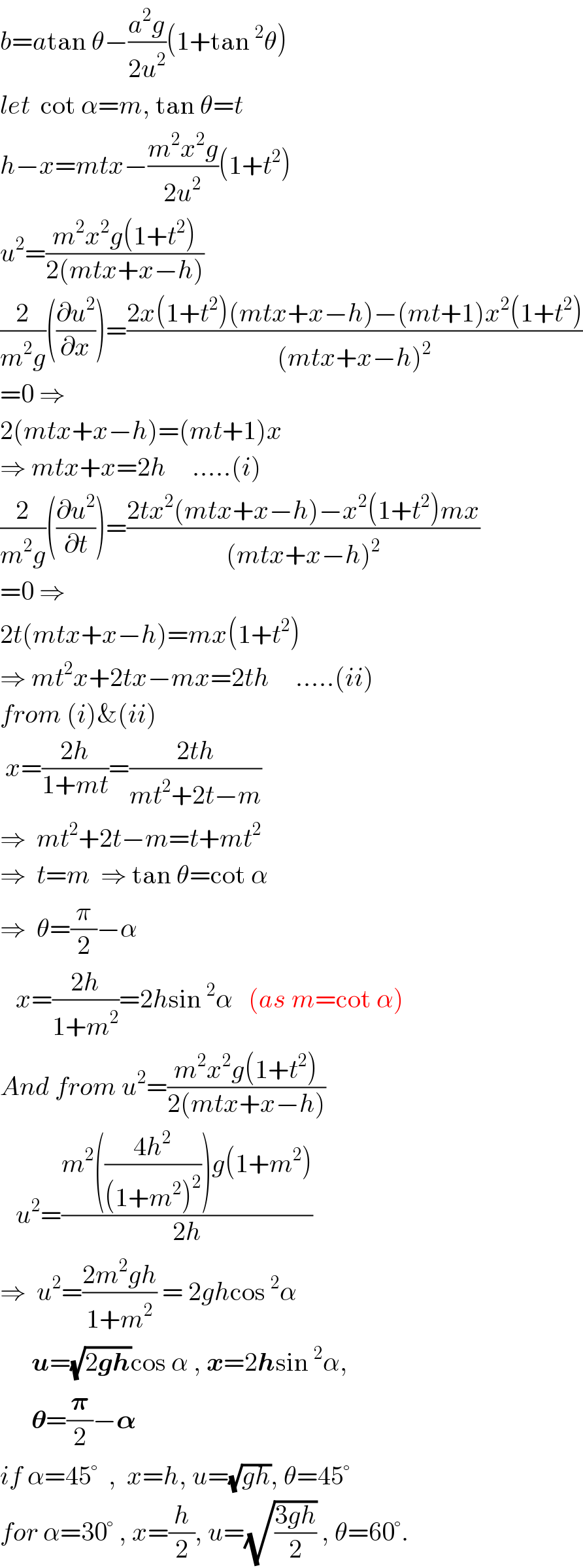
b=atan θ−((a^2 g)/(2u^2 ))(1+tan^2 θ) let cot α=m, tan θ=t h−x=mtx−((m^2 x^2 g)/(2u^2 ))(1+t^2 ) u^2 =((m^2 x^2 g(1+t^2 ))/(2(mtx+x−h))) (2/(m^2 g))((∂u^2 /∂x))=((2x(1+t^2 )(mtx+x−h)−(mt+1)x^2 (1+t^2 ))/((mtx+x−h)^2 )) =0 ⇒ 2(mtx+x−h)=(mt+1)x ⇒ mtx+x=2h .....(i) (2/(m^2 g))((∂u^2 /∂t))=((2tx^2 (mtx+x−h)−x^2 (1+t^2 )mx)/((mtx+x−h)^2 )) =0 ⇒ 2t(mtx+x−h)=mx(1+t^2 ) ⇒ mt^2 x+2tx−mx=2th .....(ii) from (i)&(ii) x=((2h)/(1+mt))=((2th)/(mt^2 +2t−m)) ⇒ mt^2 +2t−m=t+mt^2 ⇒ t=m ⇒ tan θ=cot α ⇒ θ=(π/2)−α x=((2h)/(1+m^2 ))=2hsin^2 α (as m=cot α) And from u^2 =((m^2 x^2 g(1+t^2 ))/(2(mtx+x−h))) u^2 =((m^2 (((4h^2 )/((1+m^2 )^2 )))g(1+m^2 ))/(2h)) ⇒ u^2 =((2m^2 gh)/(1+m^2 )) = 2ghcos^2 α u=(√(2gh))cos α , x=2hsin^2 α, 𝛉=(𝛑/2)−𝛂 if α=45° , x=h, u=(√(gh)), θ=45° for α=30° , x=(h/2), u=(√((3gh)/2)) , θ=60°.
$${b}={a}\mathrm{tan}\:\theta−\frac{{a}^{\mathrm{2}} {g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta\right) \\ $$$${let}\:\:\mathrm{cot}\:\alpha={m},\:\mathrm{tan}\:\theta={t} \\ $$$${h}−{x}={mtx}−\frac{{m}^{\mathrm{2}} {x}^{\mathrm{2}} {g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+{t}^{\mathrm{2}} \right) \\ $$$${u}^{\mathrm{2}} =\frac{{m}^{\mathrm{2}} {x}^{\mathrm{2}} {g}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{2}\left({mtx}+{x}−{h}\right)} \\ $$$$\frac{\mathrm{2}}{{m}^{\mathrm{2}} {g}}\left(\frac{\partial{u}^{\mathrm{2}} }{\partial{x}}\right)=\frac{\mathrm{2}{x}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({mtx}+{x}−{h}\right)−\left({mt}+\mathrm{1}\right){x}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\left({mtx}+{x}−{h}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{2}\left({mtx}+{x}−{h}\right)=\left({mt}+\mathrm{1}\right){x} \\ $$$$\Rightarrow\:{mtx}+{x}=\mathrm{2}{h}\:\:\:\:\:…..\left({i}\right) \\ $$$$\frac{\mathrm{2}}{{m}^{\mathrm{2}} {g}}\left(\frac{\partial{u}^{\mathrm{2}} }{\partial{t}}\right)=\frac{\mathrm{2}{tx}^{\mathrm{2}} \left({mtx}+{x}−{h}\right)−{x}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right){mx}}{\left({mtx}+{x}−{h}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{2}{t}\left({mtx}+{x}−{h}\right)={mx}\left(\mathrm{1}+{t}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:{mt}^{\mathrm{2}} {x}+\mathrm{2}{tx}−{mx}=\mathrm{2}{th}\:\:\:\:\:…..\left({ii}\right) \\ $$$${from}\:\left({i}\right)\&\left({ii}\right) \\ $$$$\:{x}=\frac{\mathrm{2}{h}}{\mathrm{1}+{mt}}=\frac{\mathrm{2}{th}}{{mt}^{\mathrm{2}} +\mathrm{2}{t}−{m}} \\ $$$$\Rightarrow\:\:{mt}^{\mathrm{2}} +\mathrm{2}{t}−{m}={t}+{mt}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:{t}={m}\:\:\Rightarrow\:\mathrm{tan}\:\theta=\mathrm{cot}\:\alpha \\ $$$$\Rightarrow\:\:\theta=\frac{\pi}{\mathrm{2}}−\alpha \\ $$$$\:\:\:{x}=\frac{\mathrm{2}{h}}{\mathrm{1}+{m}^{\mathrm{2}} }=\mathrm{2}{h}\mathrm{sin}\:^{\mathrm{2}} \alpha\:\:\:\left({as}\:{m}=\mathrm{cot}\:\alpha\right) \\ $$$${And}\:{from}\:{u}^{\mathrm{2}} =\frac{{m}^{\mathrm{2}} {x}^{\mathrm{2}} {g}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{2}\left({mtx}+{x}−{h}\right)} \\ $$$$\:\:\:{u}^{\mathrm{2}} =\frac{{m}^{\mathrm{2}} \left(\frac{\mathrm{4}{h}^{\mathrm{2}} }{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\mathrm{2}} }\right){g}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)}{\mathrm{2}{h}} \\ $$$$\Rightarrow\:\:{u}^{\mathrm{2}} =\frac{\mathrm{2}{m}^{\mathrm{2}} {gh}}{\mathrm{1}+{m}^{\mathrm{2}} }\:=\:\mathrm{2}{gh}\mathrm{cos}\:^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:\:\:\boldsymbol{{u}}=\sqrt{\mathrm{2}\boldsymbol{{gh}}}\mathrm{cos}\:\alpha\:,\:\boldsymbol{{x}}=\mathrm{2}\boldsymbol{{h}}\mathrm{sin}\:^{\mathrm{2}} \alpha, \\ $$$$\:\:\:\:\:\:\boldsymbol{\theta}=\frac{\boldsymbol{\pi}}{\mathrm{2}}−\boldsymbol{\alpha}\: \\ $$$${if}\:\alpha=\mathrm{45}°\:\:,\:\:{x}={h},\:{u}=\sqrt{{gh}},\:\theta=\mathrm{45}° \\ $$$${for}\:\alpha=\mathrm{30}°\:,\:{x}=\frac{{h}}{\mathrm{2}},\:{u}=\sqrt{\frac{\mathrm{3}{gh}}{\mathrm{2}}}\:,\:\theta=\mathrm{60}°. \\ $$
Commented by mr W last updated on 29/Oct/19
a=u cos θ t b=u sin θ t−(1/2)gt^2 =a tan θ−((ga^2 )/(2u^2 cos^2 θ)) (b/a)=tan θ−((ga(1+tan^2 θ))/(2u^2 )) u^2 =((ga(1+tan^2 θ))/(2(tan θ−(b/a)))) let U=((2u^2 )/(ga)), t=tan θ, λ=(b/a) ⇒U=((1+t^2 )/(t−λ)) (dU/dt)=((2t)/(t−λ))−((1+t^2 )/((t−λ)^2 ))=0 ⇒t^2 −2λt−1=0 ⇒t=λ+(√(λ^2 +1)) ⇒t^2 =2λ(λ+(√(λ^2 +1)))+1 Φ=u_(min) ^2 =((ga(λ^2 +1+λ(√(λ^2 +1))))/( (√(λ^2 +1))))=ga(λ+(√(λ^2 +1))) a=(x/(tan α)) b=h−x Φ=((gx)/(tan α))(((h−x)/x) tan α+(√((((h−x)/x))^2 tan^2 α+1))) Φ=g[h−x+(√((h−x)^2 +(x^2 /(tan^2 α))))] (dΦ/dx)=0 ((−h+(x/(sin^2 α)))/( (√((h−x)^2 +(x^2 /(tan^2 α))))))=1 ⇒x=2h sin^2 α ⇒Φ_(min) =2gh cos^2 α E_(min) =(1/2)mu^2 =(1/2)mΦ_(min) =mgh cos^2 α
$${a}={u}\:\mathrm{cos}\:\theta\:{t} \\ $$$${b}={u}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} ={a}\:\mathrm{tan}\:\theta−\frac{{ga}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\frac{{b}}{{a}}=\mathrm{tan}\:\theta−\frac{{ga}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$${u}^{\mathrm{2}} =\frac{{ga}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}\left(\mathrm{tan}\:\theta−\frac{{b}}{{a}}\right)} \\ $$$${let}\:{U}=\frac{\mathrm{2}{u}^{\mathrm{2}} }{{ga}},\:{t}=\mathrm{tan}\:\theta,\:\lambda=\frac{{b}}{{a}} \\ $$$$\Rightarrow{U}=\frac{\mathrm{1}+{t}^{\mathrm{2}} }{{t}−\lambda} \\ $$$$\frac{{dU}}{{dt}}=\frac{\mathrm{2}{t}}{{t}−\lambda}−\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\left({t}−\lambda\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{2}} −\mathrm{2}\lambda{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}=\lambda+\sqrt{\lambda^{\mathrm{2}} +\mathrm{1}} \\ $$$$\Rightarrow{t}^{\mathrm{2}} =\mathrm{2}\lambda\left(\lambda+\sqrt{\lambda^{\mathrm{2}} +\mathrm{1}}\right)+\mathrm{1} \\ $$$$\Phi={u}_{{min}} ^{\mathrm{2}} =\frac{{ga}\left(\lambda^{\mathrm{2}} +\mathrm{1}+\lambda\sqrt{\lambda^{\mathrm{2}} +\mathrm{1}}\right)}{\:\sqrt{\lambda^{\mathrm{2}} +\mathrm{1}}}={ga}\left(\lambda+\sqrt{\lambda^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$${a}=\frac{{x}}{\mathrm{tan}\:\alpha} \\ $$$${b}={h}−{x} \\ $$$$\Phi=\frac{{gx}}{\mathrm{tan}\:\alpha}\left(\frac{{h}−{x}}{{x}}\:\mathrm{tan}\:\alpha+\sqrt{\left(\frac{{h}−{x}}{{x}}\right)^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\alpha+\mathrm{1}}\right) \\ $$$$\Phi={g}\left[{h}−{x}+\sqrt{\left({h}−{x}\right)^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} }{\mathrm{tan}^{\mathrm{2}} \:\alpha}}\right] \\ $$$$\frac{{d}\Phi}{{dx}}=\mathrm{0} \\ $$$$\frac{−{h}+\frac{{x}}{\mathrm{sin}^{\mathrm{2}} \:\alpha}}{\:\sqrt{\left({h}−{x}\right)^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} }{\mathrm{tan}^{\mathrm{2}} \:\alpha}}}=\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{2}{h}\:\mathrm{sin}^{\mathrm{2}} \:\alpha \\ $$$$\Rightarrow\Phi_{{min}} =\mathrm{2}{gh}\:\mathrm{cos}^{\mathrm{2}} \:\alpha \\ $$$${E}_{{min}} =\frac{\mathrm{1}}{\mathrm{2}}{mu}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{m}\Phi_{{min}} ={mgh}\:\mathrm{cos}^{\mathrm{2}} \:\alpha \\ $$
Commented by ajfour last updated on 30/Oct/19
Thanks Sir. i corrected.
$$\mathcal{T}{hanks}\:{Sir}.\:{i}\:{corrected}. \\ $$
Commented by mr W last updated on 30/Oct/19
Commented by mr W last updated on 30/Oct/19
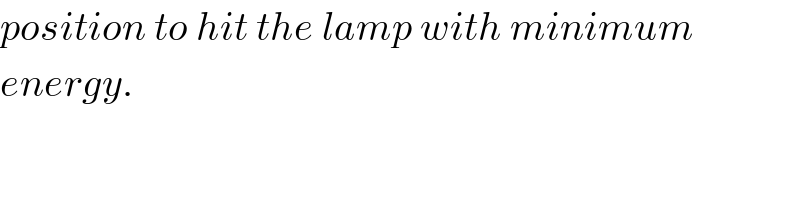
position to hit the lamp with minimum energy.
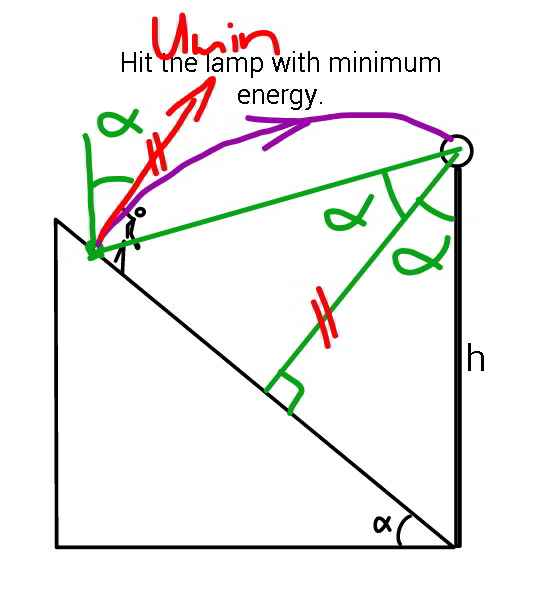
$${position}\:{to}\:{hit}\:{the}\:{lamp}\:{with}\:{minimum} \\ $$$${energy}. \\ $$
Commented by ajfour last updated on 30/Oct/19
Great interpretation Sir, thanks a lot. (should have been a classical question:)
$${Great}\:{interpretation}\:{Sir},\:{thanks} \\ $$$${a}\:{lot}.\:\left({should}\:{have}\:{been}\:{a}\right. \\ $$$$\left.{classical}\:{question}:\right) \\ $$
Commented by mr W last updated on 30/Oct/19
nice question!
$${nice}\:{question}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *