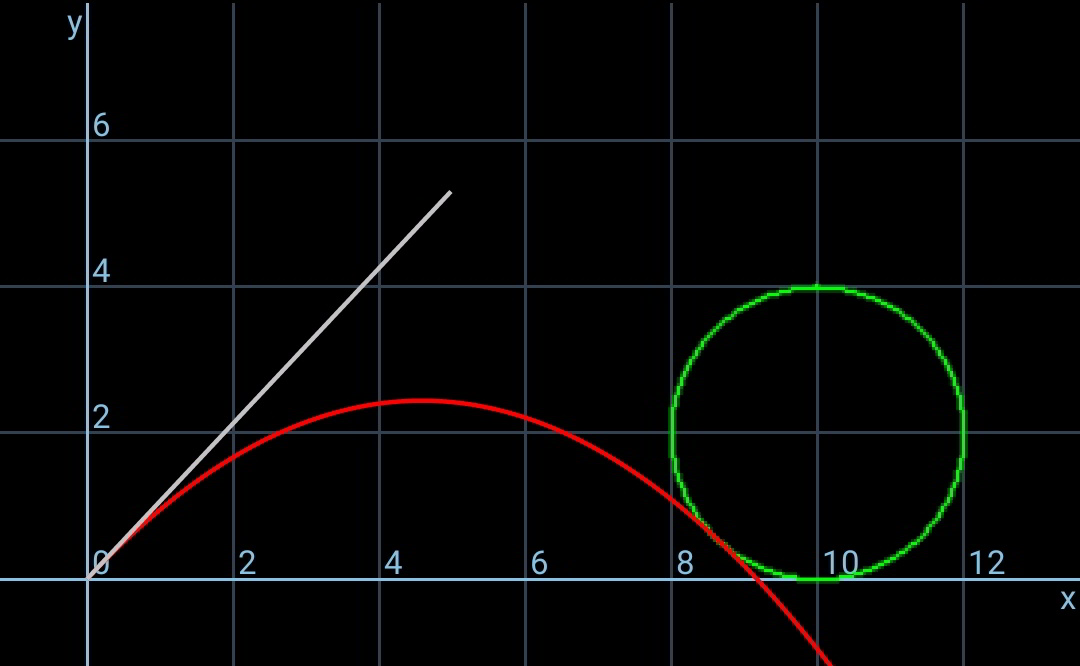
Question Number 72563 by ajfour last updated on 30/Oct/19
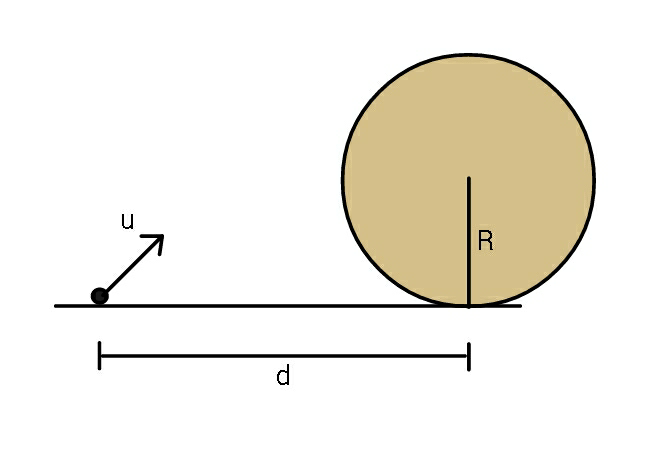
Commented by ajfour last updated on 30/Oct/19
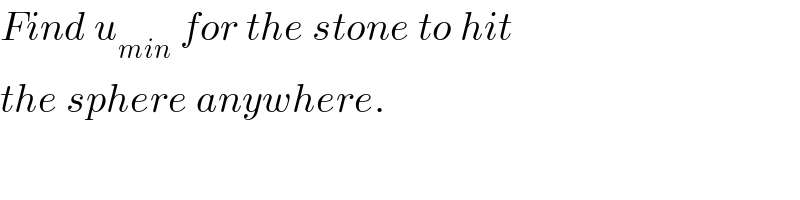
$${Find}\:{u}_{{min}} \:{for}\:{the}\:{stone}\:{to}\:{hit} \\ $$$${the}\:{sphere}\:{anywhere}. \\ $$
Answered by mr W last updated on 30/Oct/19
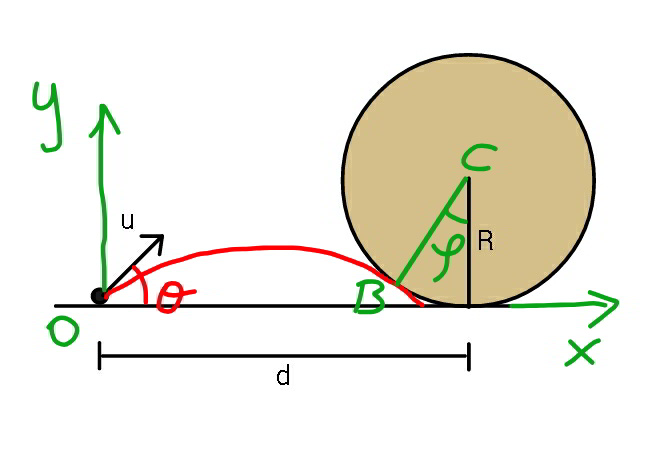
Commented by mr W last updated on 30/Oct/19
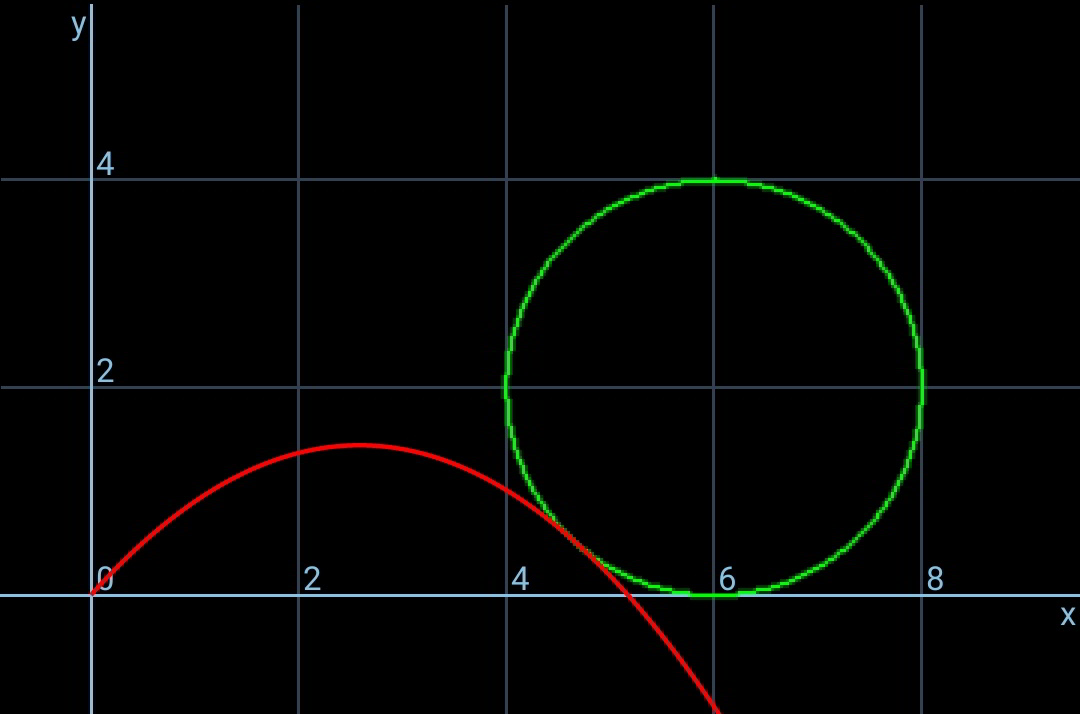
![x=u cos θ t y=u sin θ t−((gt^2 )/2) y=x tan θ−((g(1+tan^2 θ)x^2 )/(2u^2 )) with t=tan θ ⇒y=tx−((g(1+t^2 )x^2 )/(2u^2 )) y′=t−((g(1+t^2 )x)/u^2 ) at point B(d−R sin ϕ, R(1−cos ϕ)): R(1−cos ϕ)=t(d−R sin ϕ)−((g(1+t^2 )(d−R sin ϕ)^2 )/(2u^2 )) ...(i) −tan ϕ=t−((g(1+t^2 )(d−R sin ϕ))/u^2 ) ...(ii) ⇒((g(1+t^2 )(d−R sin ϕ))/u^2 )=t+tan ϕ R(1−cos ϕ)=t(d−R sin ϕ)−(((d−R sin ϕ)(t+tan ϕ))/2) with δ=(d/R) ⇒t=tan ϕ+((2(1−cos ϕ))/(δ−sin ϕ)) ⇒((gR)/u^2 )=((t+tan ϕ)/((δ−sin ϕ)(1+t^2 ))) let U=((gR)/(2u^2 )) ⇒2U=((t+tan ϕ)/((δ−sin ϕ)(1+t^2 ))) ⇒2U=((2 tan ϕ+((2(1−cos ϕ))/(δ−sin ϕ)))/((δ−sin ϕ)[1+(tan ϕ+((2(1−cos ϕ))/(δ−sin ϕ)))^2 ])) ⇒U=((1−cos ϕ+(δ−sin ϕ) tan ϕ)/((δ−sin ϕ)^2 +[(δ−sin ϕ) tan ϕ+2(1−cos ϕ)]^2 )) (dU/dϕ)=0 ⇒ ϕ ⇒ U_(max) ⇒ u_(min) example: δ=(d/R)=(6/2)=3 ⇒ϕ=0.7309 ⇒U_(max) =0.1922 ⇒u_(min) =1.613(√(gR))](https://www.tinkutara.com/question/Q72580.png)
$${x}={u}\:\mathrm{cos}\:\theta\:{t} \\ $$$${y}={u}\:\mathrm{sin}\:\theta\:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${y}={x}\:\mathrm{tan}\:\theta−\frac{{g}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right){x}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$${with}\:{t}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow{y}={tx}−\frac{{g}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right){x}^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$${y}'={t}−\frac{{g}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}}{{u}^{\mathrm{2}} } \\ $$$${at}\:{point}\:{B}\left({d}−{R}\:\mathrm{sin}\:\varphi,\:{R}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)\right): \\ $$$${R}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)={t}\left({d}−{R}\:\mathrm{sin}\:\varphi\right)−\frac{{g}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left({d}−{R}\:\mathrm{sin}\:\varphi\right)^{\mathrm{2}} }{\mathrm{2}{u}^{\mathrm{2}} }\:\:\:…\left({i}\right) \\ $$$$−\mathrm{tan}\:\varphi={t}−\frac{{g}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({d}−{R}\:\mathrm{sin}\:\varphi\right)}{{u}^{\mathrm{2}} }\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\frac{{g}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({d}−{R}\:\mathrm{sin}\:\varphi\right)}{{u}^{\mathrm{2}} }={t}+\mathrm{tan}\:\varphi \\ $$$${R}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)={t}\left({d}−{R}\:\mathrm{sin}\:\varphi\right)−\frac{\left({d}−{R}\:\mathrm{sin}\:\varphi\right)\left({t}+\mathrm{tan}\:\varphi\right)}{\mathrm{2}} \\ $$$${with}\:\delta=\frac{{d}}{{R}} \\ $$$$\Rightarrow{t}=\mathrm{tan}\:\varphi+\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)}{\delta−\mathrm{sin}\:\varphi} \\ $$$$\Rightarrow\frac{{gR}}{{u}^{\mathrm{2}} }=\frac{{t}+\mathrm{tan}\:\varphi}{\left(\delta−\mathrm{sin}\:\varphi\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$${let}\:{U}=\frac{{gR}}{\mathrm{2}{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2}{U}=\frac{{t}+\mathrm{tan}\:\varphi}{\left(\delta−\mathrm{sin}\:\varphi\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{2}{U}=\frac{\mathrm{2}\:\mathrm{tan}\:\varphi+\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)}{\delta−\mathrm{sin}\:\varphi}}{\left(\delta−\mathrm{sin}\:\varphi\right)\left[\mathrm{1}+\left(\mathrm{tan}\:\varphi+\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)}{\delta−\mathrm{sin}\:\varphi}\right)^{\mathrm{2}} \right]} \\ $$$$\Rightarrow{U}=\frac{\mathrm{1}−\mathrm{cos}\:\varphi+\left(\delta−\mathrm{sin}\:\varphi\right)\:\mathrm{tan}\:\varphi}{\left(\delta−\mathrm{sin}\:\varphi\right)^{\mathrm{2}} +\left[\left(\delta−\mathrm{sin}\:\varphi\right)\:\mathrm{tan}\:\varphi+\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right)\right]^{\mathrm{2}} } \\ $$$$\frac{{dU}}{{d}\varphi}=\mathrm{0}\:\Rightarrow\:\varphi\:\Rightarrow\:{U}_{{max}} \Rightarrow\:{u}_{{min}} \\ $$$$ \\ $$$${example}: \\ $$$$\delta=\frac{{d}}{{R}}=\frac{\mathrm{6}}{\mathrm{2}}=\mathrm{3} \\ $$$$\Rightarrow\varphi=\mathrm{0}.\mathrm{7309} \\ $$$$\Rightarrow{U}_{{max}} =\mathrm{0}.\mathrm{1922}\:\Rightarrow{u}_{{min}} =\mathrm{1}.\mathrm{613}\sqrt{{gR}} \\ $$
Commented by mr W last updated on 30/Oct/19
Commented by ajfour last updated on 30/Oct/19

$${Thanks}\:{Sir},\:{but}\:{lets}\:{see}\:{if}\:{a} \\ $$$${final}\:{answer}\:{be}\:{possible}.. \\ $$
Commented by malwaan last updated on 30/Oct/19

$$\boldsymbol{{I}}\:\boldsymbol{{think}} \\ $$$$\boldsymbol{{u}}_{\boldsymbol{{max}}} \:\boldsymbol{{at}}\:\boldsymbol{\theta}=\:\mathrm{45}^{°} \\ $$
Commented by mr W last updated on 30/Oct/19

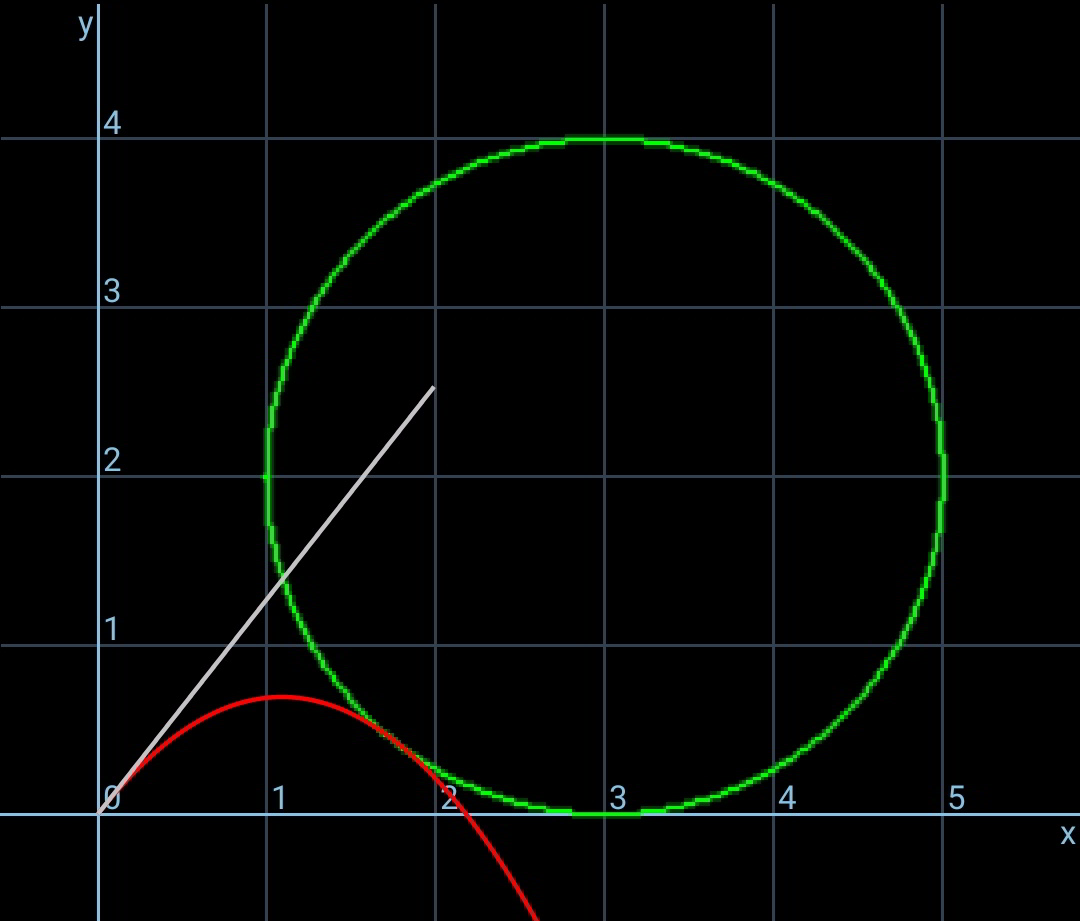
$${it}\:{is}\:{to}\:{find}\:{a}\:{parabola}\:{which}\:{tangents} \\ $$$${the}\:{circle}\:{AND}\:{has}\:{the}\:{minimum} \\ $$$${energy}.\:\theta\:{is}\:{not}\:{a}\:{constant},\:{but} \\ $$$${depends}\:{on}\:{the}\:{position}\:{of}\:{the}\:{circle}. \\ $$
Commented by mr W last updated on 30/Oct/19
Commented by mr W last updated on 30/Oct/19