Question Number 72606 by TawaTawa last updated on 30/Oct/19
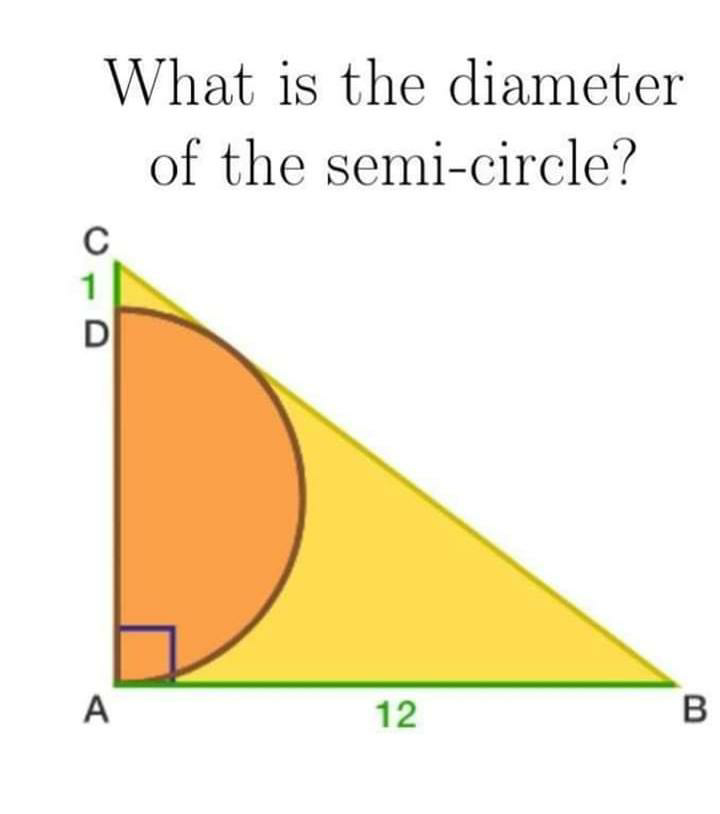
Answered by mr W last updated on 30/Oct/19
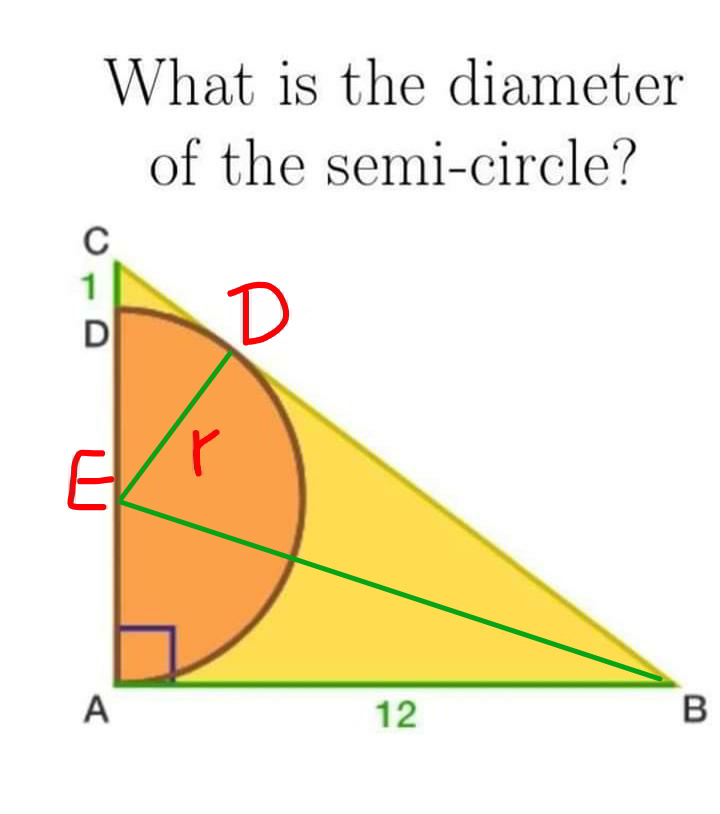
Commented by mr W last updated on 30/Oct/19
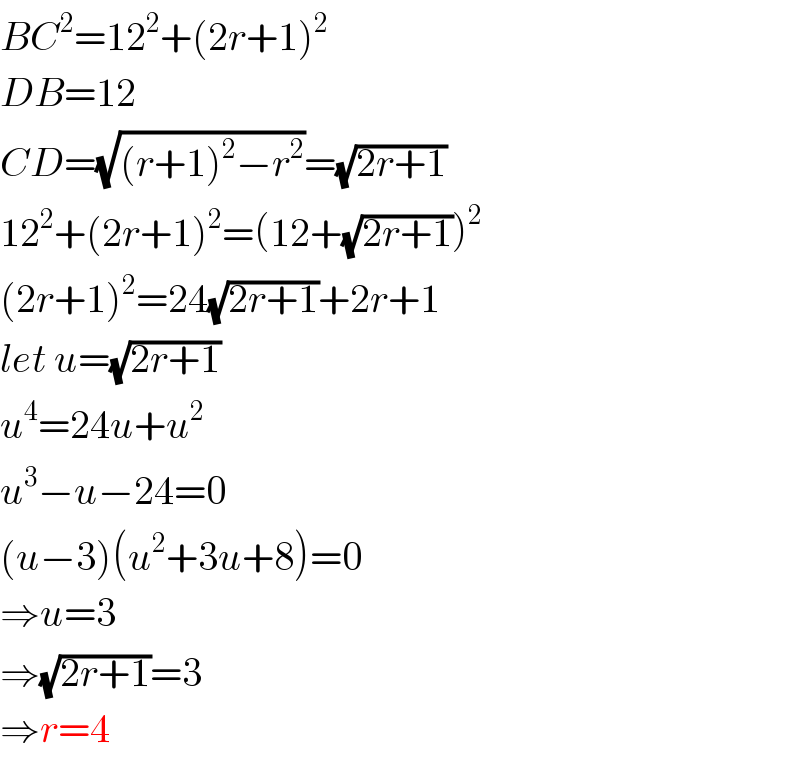
$${BC}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} +\left(\mathrm{2}{r}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${DB}=\mathrm{12} \\ $$$${CD}=\sqrt{\left({r}+\mathrm{1}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{\mathrm{2}{r}+\mathrm{1}} \\ $$$$\mathrm{12}^{\mathrm{2}} +\left(\mathrm{2}{r}+\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{12}+\sqrt{\mathrm{2}{r}+\mathrm{1}}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{2}{r}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{24}\sqrt{\mathrm{2}{r}+\mathrm{1}}+\mathrm{2}{r}+\mathrm{1} \\ $$$${let}\:{u}=\sqrt{\mathrm{2}{r}+\mathrm{1}} \\ $$$${u}^{\mathrm{4}} =\mathrm{24}{u}+{u}^{\mathrm{2}} \\ $$$${u}^{\mathrm{3}} −{u}−\mathrm{24}=\mathrm{0} \\ $$$$\left({u}−\mathrm{3}\right)\left({u}^{\mathrm{2}} +\mathrm{3}{u}+\mathrm{8}\right)=\mathrm{0} \\ $$$$\Rightarrow{u}=\mathrm{3} \\ $$$$\Rightarrow\sqrt{\mathrm{2}{r}+\mathrm{1}}=\mathrm{3} \\ $$$$\Rightarrow{r}=\mathrm{4} \\ $$
Commented by TawaTawa last updated on 30/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by Tanmay chaudhury last updated on 30/Oct/19

$${circle}\:{x}^{\mathrm{2}} +\left({y}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\frac{{x}}{\mathrm{12}}+\frac{{y}}{\mathrm{2}{r}+\mathrm{1}}=\mathrm{1}\:{is}\:{tangent}\rightarrow{BC} \\ $$$${distance}\:{from}\left(\mathrm{0},{r}\right)\:{to}\:{BC}\:{is}\:{radius} \\ $$$$\left(\mathrm{2}{r}+\mathrm{1}\right){x}+\mathrm{12}{y}−\mathrm{12}\left(\mathrm{2}{r}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mid\frac{\left(\mathrm{2}{r}+\mathrm{1}\right)×\mathrm{0}+\mathrm{12}\left({r}\right)−\mathrm{24}{r}−\mathrm{12}}{\:\sqrt{\left(\mathrm{2}{r}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }}\mid={r} \\ $$$$−\mathrm{12}{r}−\mathrm{12}={r}×\sqrt{\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{r}+\mathrm{1}+\mathrm{144}}\: \\ $$$$\mathrm{144}{r}^{\mathrm{2}} +\mathrm{144}+\mathrm{288}{r}=\mathrm{4}{r}^{\mathrm{4}} +\mathrm{4}{r}^{\mathrm{3}} +\mathrm{145}{r}^{\mathrm{2}} \\ $$$$\mathrm{4}{r}^{\mathrm{4}} +\mathrm{4}{r}^{\mathrm{3}} +{r}^{\mathrm{2}} −\mathrm{288}{r}−\mathrm{144}=\mathrm{0} \\ $$$${r}^{\mathrm{2}} \left(\mathrm{4}{r}^{\mathrm{2}} +\mathrm{4}{r}+\mathrm{1}\right)−\mathrm{144}\left(\mathrm{2}{r}+\mathrm{1}\right)=\mathrm{0} \\ $$$${r}^{\mathrm{2}} \left(\mathrm{2}{r}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{144}\left(\mathrm{2}{r}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{r}+\mathrm{1}\right)\left(\mathrm{2}{r}^{\mathrm{3}} +{r}^{\mathrm{2}} −\mathrm{144}\right)=\mathrm{0} \\ $$$${r}\neq−\mathrm{0}.\mathrm{5} \\ $$$$\mathrm{2}{r}^{\mathrm{3}} +{r}^{\mathrm{2}} −\mathrm{128}−\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{2}\left({r}^{\mathrm{3}} −\mathrm{64}\right)+\left({r}+\mathrm{4}\right)\left({r}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\mathrm{2}\left({r}−\mathrm{4}\right)\left({r}^{\mathrm{2}} +\mathrm{4}{r}+\mathrm{16}\right)+\left({r}+\mathrm{4}\right)\left({r}−\mathrm{4}\right)=\mathrm{0} \\ $$$$\left({r}−\mathrm{4}\right)\left(\mathrm{2}{r}^{\mathrm{2}} +\mathrm{8}{r}+\mathrm{32}+{r}+\mathrm{4}\right)=\mathrm{0} \\ $$$${so}\:\:{r}=\mathrm{4}\:{answer} \\ $$
Commented by TawaTawa last updated on 30/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
