Menu Close

Question-72672

Tinku Tara 0 Comments
Pin




Question Number 72672 by mr W last updated on 31/Oct/19
Commented by mr W last updated on 31/Oct/19
find u_(min) for the stone to hit the ground behind the sphere. (see also Q72563, with thanks to ajfour sir for the orginal question)
$${find}\:{u}_{{min}} \:{for}\:{the}\:{stone}\:{to}\:{hit}\:{the} \\ $$$${ground}\:{behind}\:{the}\:{sphere}. \\ $$$$\left({see}\:{also}\:{Q}\mathrm{72563},\:{with}\:{thanks}\:{to}\:\right. \\ $$$$\left.{ajfour}\:{sir}\:{for}\:{the}\:{orginal}\:{question}\right) \\ $$
Commented by malwaan last updated on 31/Oct/19
very easy !
$$\boldsymbol{{very}}\:\boldsymbol{{easy}}\:! \\ $$
Answered by ajfour last updated on 31/Oct/19
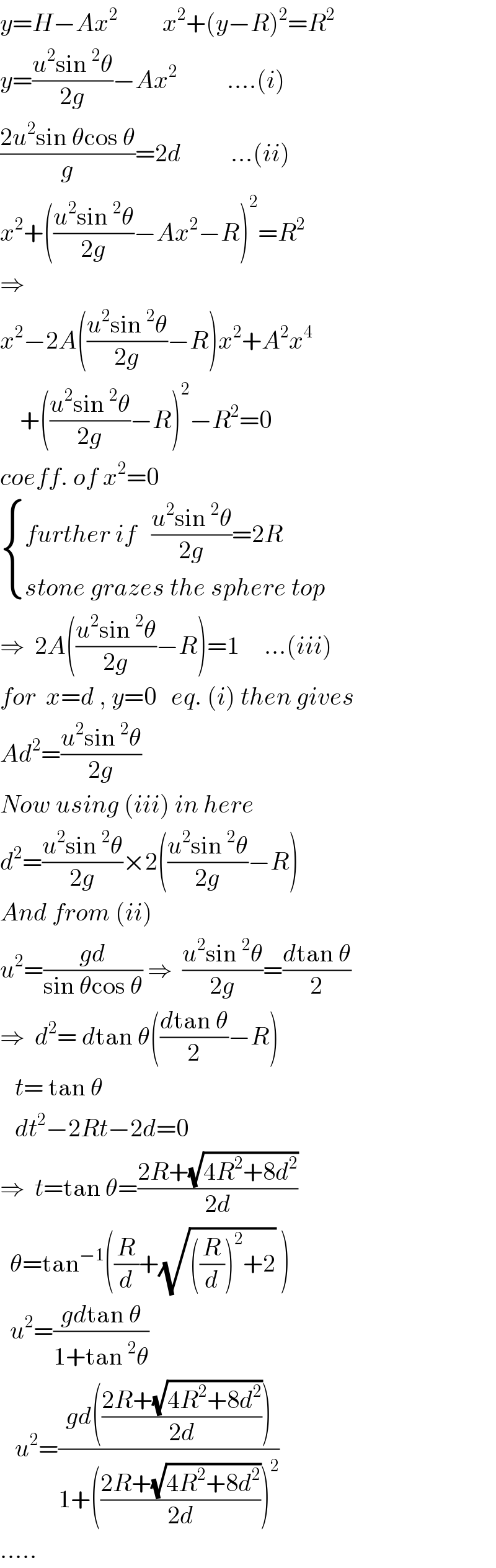
y=H−Ax^2 x^2 +(y−R)^2 =R^2 y=((u^2 sin^2 θ)/(2g))−Ax^2 ....(i) ((2u^2 sin θcos θ)/g)=2d ...(ii) x^2 +(((u^2 sin^2 θ)/(2g))−Ax^2 −R)^2 =R^2 ⇒ x^2 −2A(((u^2 sin^2 θ)/(2g))−R)x^2 +A^2 x^4 +(((u^2 sin^2 θ)/(2g))−R)^2 −R^2 =0 coeff. of x^2 =0 { ((further if ((u^2 sin^2 θ)/(2g))=2R)),((stone grazes the sphere top)) :} ⇒ 2A(((u^2 sin^2 θ)/(2g))−R)=1 ...(iii) for x=d , y=0 eq. (i) then gives Ad^2 =((u^2 sin^2 θ)/(2g)) Now using (iii) in here d^2 =((u^2 sin^2 θ)/(2g))×2(((u^2 sin^2 θ)/(2g))−R) And from (ii) u^2 =((gd)/(sin θcos θ)) ⇒ ((u^2 sin^2 θ)/(2g))=((dtan θ)/2) ⇒ d^2 = dtan θ(((dtan θ)/2)−R) t= tan θ dt^2 −2Rt−2d=0 ⇒ t=tan θ=((2R+(√(4R^2 +8d^2 )))/(2d)) θ=tan^(−1) ((R/d)+(√(((R/d))^2 +2)) ) u^2 =((gdtan θ)/(1+tan^2 θ)) u^2 =((gd(((2R+(√(4R^2 +8d^2 )))/(2d))))/(1+(((2R+(√(4R^2 +8d^2 )))/(2d)))^2 )) .....
$${y}={H}−{Ax}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} +\left({y}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${y}=\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}−{Ax}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:….\left({i}\right) \\ $$$$\frac{\mathrm{2}{u}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{{g}}=\mathrm{2}{d}\:\:\:\:\:\:\:\:\:\:…\left({ii}\right) \\ $$$${x}^{\mathrm{2}} +\left(\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}−{Ax}^{\mathrm{2}} −{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{A}\left(\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}−{R}\right){x}^{\mathrm{2}} +{A}^{\mathrm{2}} {x}^{\mathrm{4}} \\ $$$$\:\:\:\:+\left(\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}−{R}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} =\mathrm{0} \\ $$$${coeff}.\:{of}\:{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\begin{cases}{{further}\:{if}\:\:\:\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}=\mathrm{2}{R}}\\{{stone}\:{grazes}\:{the}\:{sphere}\:{top}}\end{cases} \\ $$$$\Rightarrow\:\:\mathrm{2}{A}\left(\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}−{R}\right)=\mathrm{1}\:\:\:\:\:…\left({iii}\right) \\ $$$${for}\:\:{x}={d}\:,\:{y}=\mathrm{0}\:\:\:{eq}.\:\left({i}\right)\:{then}\:{gives} \\ $$$${Ad}^{\mathrm{2}} =\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}} \\ $$$${Now}\:{using}\:\left({iii}\right)\:{in}\:{here} \\ $$$${d}^{\mathrm{2}} =\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}×\mathrm{2}\left(\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}−{R}\right) \\ $$$${And}\:{from}\:\left({ii}\right) \\ $$$${u}^{\mathrm{2}} =\frac{{gd}}{\mathrm{sin}\:\theta\mathrm{cos}\:\theta}\:\Rightarrow\:\:\frac{{u}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}{\mathrm{2}{g}}=\frac{{d}\mathrm{tan}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\:\:{d}^{\mathrm{2}} =\:{d}\mathrm{tan}\:\theta\left(\frac{{d}\mathrm{tan}\:\theta}{\mathrm{2}}−{R}\right) \\ $$$$\:\:\:{t}=\:\mathrm{tan}\:\theta \\ $$$$\:\:\:{dt}^{\mathrm{2}} −\mathrm{2}{Rt}−\mathrm{2}{d}=\mathrm{0} \\ $$$$\Rightarrow\:\:{t}=\mathrm{tan}\:\theta=\frac{\mathrm{2}{R}+\sqrt{\mathrm{4}{R}^{\mathrm{2}} +\mathrm{8}{d}^{\mathrm{2}} }}{\mathrm{2}{d}} \\ $$$$\:\:\theta=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{R}}{{d}}+\sqrt{\left(\frac{{R}}{{d}}\right)^{\mathrm{2}} +\mathrm{2}}\:\right) \\ $$$$\:\:{u}^{\mathrm{2}} =\frac{{gd}\mathrm{tan}\:\theta}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta} \\ $$$$\:\:\:{u}^{\mathrm{2}} =\frac{{gd}\left(\frac{\mathrm{2}{R}+\sqrt{\mathrm{4}{R}^{\mathrm{2}} +\mathrm{8}{d}^{\mathrm{2}} }}{\mathrm{2}{d}}\right)}{\mathrm{1}+\left(\frac{\mathrm{2}{R}+\sqrt{\mathrm{4}{R}^{\mathrm{2}} +\mathrm{8}{d}^{\mathrm{2}} }}{\mathrm{2}{d}}\right)^{\mathrm{2}} } \\ $$$$….. \\ $$
Answered by mr W last updated on 31/Oct/19
Commented by mr W last updated on 31/Oct/19
there are many different cases. what the image shows is the situation when the sphere is far away. if the sphere is near from the origin, it could look differently. my method can not treat such cases correctly. your solution is for such cases then.
$${there}\:{are}\:{many}\:{different}\:{cases}.\:{what} \\ $$$${the}\:{image}\:{shows}\:{is}\:{the}\:{situation}\:{when} \\ $$$${the}\:{sphere}\:{is}\:{far}\:{away}.\:{if}\:{the}\:{sphere} \\ $$$${is}\:{near}\:{from}\:{the}\:{origin},\:{it}\:{could}\:{look} \\ $$$${differently}.\:{my}\:{method}\:{can}\:{not} \\ $$$${treat}\:{such}\:{cases}\:{correctly}.\:{your}\:{solution} \\ $$$${is}\:{for}\:{such}\:{cases}\:{then}. \\ $$
Commented by mr W last updated on 31/Oct/19
x=u cos θ t y=u sin θ t−((gt^2 )/2) y=x tan θ−(g/(2u^2 ))(1+tan^2 θ)x^2 let t=tan θ y=tx−(g/(2u^2 ))(1+t^2 )x^2 y′=t−((g(1+t^2 )x)/u^2 ) B(d+R sin ϕ, R(1+cos ϕ)) −tan ϕ=t−((g(1+t^2 )(d+R sin ϕ))/u^2 ) ⇒((g(1+t^2 )(d+R sin ϕ))/u^2 )=t+tan ϕ R(1+cos ϕ)=t(d+R sin ϕ)−(g/(2u^2 ))(1+t^2 )(d+R sin ϕ)^2 R(1+cos ϕ)=t(d+R sin ϕ)−(((d+R sin ϕ)(t+tan ϕ))/2) ⇒t=tan ϕ+((2(1+cos ϕ))/(δ+sin ϕ)) with δ=(d/R) ⇒((gR(1+t^2 )(δ+sin ϕ))/u^2 )=t+tan ϕ ⇒((gR)/u^2 )=((t+tan ϕ)/((δ+sin ϕ)(1+t^2 ))) ⇒((gR)/(2u^2 ))=U=((1+cos ϕ+(δ+sin ϕ)tan ϕ)/((δ+sin ϕ)^2 +[(δ+sin ϕ)tan ϕ+2(1+cos ϕ)]^2 )) (dU/dϕ)=0 .....
$${x}={u}\:\mathrm{cos}\:\theta\:{t} \\ $$$${y}={u}\:\mathrm{sin}\:\theta\:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${y}={x}\:\mathrm{tan}\:\theta−\frac{{g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right){x}^{\mathrm{2}} \\ $$$${let}\:{t}=\mathrm{tan}\:\theta \\ $$$${y}={tx}−\frac{{g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right){x}^{\mathrm{2}} \\ $$$${y}'={t}−\frac{{g}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){x}}{{u}^{\mathrm{2}} } \\ $$$${B}\left({d}+{R}\:\mathrm{sin}\:\varphi,\:{R}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)\right) \\ $$$$−\mathrm{tan}\:\varphi={t}−\frac{{g}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({d}+{R}\:\mathrm{sin}\:\varphi\right)}{{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{g}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({d}+{R}\:\mathrm{sin}\:\varphi\right)}{{u}^{\mathrm{2}} }={t}+\mathrm{tan}\:\varphi \\ $$$${R}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)={t}\left({d}+{R}\:\mathrm{sin}\:\varphi\right)−\frac{{g}}{\mathrm{2}{u}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left({d}+{R}\:\mathrm{sin}\:\varphi\right)^{\mathrm{2}} \\ $$$${R}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)={t}\left({d}+{R}\:\mathrm{sin}\:\varphi\right)−\frac{\left({d}+{R}\:\mathrm{sin}\:\varphi\right)\left({t}+\mathrm{tan}\:\varphi\right)}{\mathrm{2}} \\ $$$$\Rightarrow{t}=\mathrm{tan}\:\varphi+\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)}{\delta+\mathrm{sin}\:\varphi}\:{with}\:\delta=\frac{{d}}{{R}} \\ $$$$\Rightarrow\frac{{gR}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\delta+\mathrm{sin}\:\varphi\right)}{{u}^{\mathrm{2}} }={t}+\mathrm{tan}\:\varphi \\ $$$$\Rightarrow\frac{{gR}}{{u}^{\mathrm{2}} }=\frac{{t}+\mathrm{tan}\:\varphi}{\left(\delta+\mathrm{sin}\:\varphi\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\frac{{gR}}{\mathrm{2}{u}^{\mathrm{2}} }={U}=\frac{\mathrm{1}+\mathrm{cos}\:\varphi+\left(\delta+\mathrm{sin}\:\varphi\right)\mathrm{tan}\:\varphi}{\left(\delta+\mathrm{sin}\:\varphi\right)^{\mathrm{2}} +\left[\left(\delta+\mathrm{sin}\:\varphi\right)\mathrm{tan}\:\varphi+\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\varphi\right)\right]^{\mathrm{2}} } \\ $$$$\frac{{dU}}{{d}\varphi}=\mathrm{0}\:….. \\ $$
Commented by mr W last updated on 31/Oct/19
Commented by ajfour last updated on 31/Oct/19
should it be this way, i was mistaken then sir, i thought the trajectory would be envelop the sphere symmetrically.
$${should}\:{it}\:{be}\:{this}\:{way},\:{i}\:{was}\: \\ $$$${mistaken}\:{then}\:{sir},\:{i}\:{thought} \\ $$$${the}\:{trajectory}\:{would}\:{be}\:{envelop} \\ $$$${the}\:{sphere}\:{symmetrically}. \\ $$
Commented by mr W last updated on 31/Oct/19

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *