Menu Close

Question-72836

Tinku Tara 0 Comments
Pin




Question Number 72836 by aliesam last updated on 03/Nov/19
Commented by mathmax by abdo last updated on 04/Nov/19
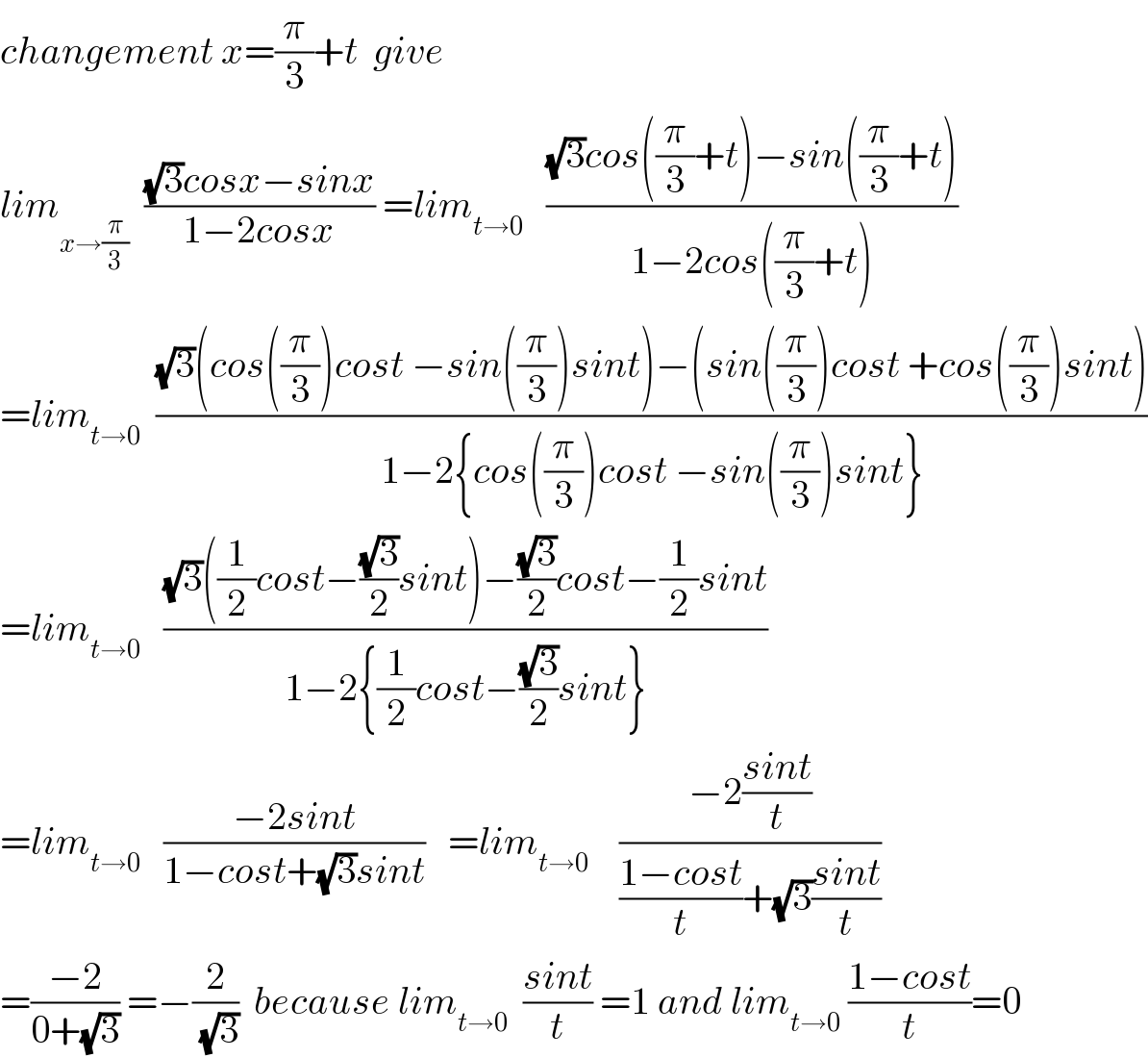
changement x=(π/3)+t give lim_(x→(π/3)) (((√3)cosx−sinx)/(1−2cosx)) =lim_(t→0) (((√3)cos((π/3)+t)−sin((π/3)+t))/(1−2cos((π/3)+t))) =lim_(t→0) (((√3)(cos((π/3))cost −sin((π/3))sint)−(sin((π/3))cost +cos((π/3))sint))/(1−2{cos((π/3))cost −sin((π/3))sint})) =lim_(t→0) (((√3)((1/2)cost−((√3)/2)sint)−((√3)/2)cost−(1/2)sint)/(1−2{(1/2)cost−((√3)/2)sint})) =lim_(t→0) ((−2sint)/(1−cost+(√3)sint)) =lim_(t→0) ((−2((sint)/t))/(((1−cost)/t)+(√3)((sint)/t))) =((−2)/(0+(√3))) =−(2/( (√3))) because lim_(t→0) ((sint)/t) =1 and lim_(t→0) ((1−cost)/t)=0
$${changement}\:{x}=\frac{\pi}{\mathrm{3}}+{t}\:\:{give} \\ $$$${lim}_{{x}\rightarrow\frac{\pi}{\mathrm{3}}} \:\:\frac{\sqrt{\mathrm{3}}{cosx}−{sinx}}{\mathrm{1}−\mathrm{2}{cosx}}\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{\sqrt{\mathrm{3}}{cos}\left(\frac{\pi}{\mathrm{3}}+{t}\right)−{sin}\left(\frac{\pi}{\mathrm{3}}+{t}\right)}{\mathrm{1}−\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}+{t}\right)} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\frac{\sqrt{\mathrm{3}}\left({cos}\left(\frac{\pi}{\mathrm{3}}\right){cost}\:−{sin}\left(\frac{\pi}{\mathrm{3}}\right){sint}\right)−\left({sin}\left(\frac{\pi}{\mathrm{3}}\right){cost}\:+{cos}\left(\frac{\pi}{\mathrm{3}}\right){sint}\right)}{\mathrm{1}−\mathrm{2}\left\{{cos}\left(\frac{\pi}{\mathrm{3}}\right){cost}\:−{sin}\left(\frac{\pi}{\mathrm{3}}\right){sint}\right\}} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{\sqrt{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}{cost}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sint}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cost}−\frac{\mathrm{1}}{\mathrm{2}}{sint}}{\mathrm{1}−\mathrm{2}\left\{\frac{\mathrm{1}}{\mathrm{2}}{cost}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sint}\right\}} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{−\mathrm{2}{sint}}{\mathrm{1}−{cost}+\sqrt{\mathrm{3}}{sint}}\:\:\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\:\frac{−\mathrm{2}\frac{{sint}}{{t}}}{\frac{\mathrm{1}−{cost}}{{t}}+\sqrt{\mathrm{3}}\frac{{sint}}{{t}}} \\ $$$$=\frac{−\mathrm{2}}{\mathrm{0}+\sqrt{\mathrm{3}}}\:=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\:{because}\:{lim}_{{t}\rightarrow\mathrm{0}} \:\:\frac{{sint}}{{t}}\:=\mathrm{1}\:{and}\:{lim}_{{t}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}−{cost}}{{t}}=\mathrm{0} \\ $$
Answered by $@ty@m123 last updated on 04/Nov/19
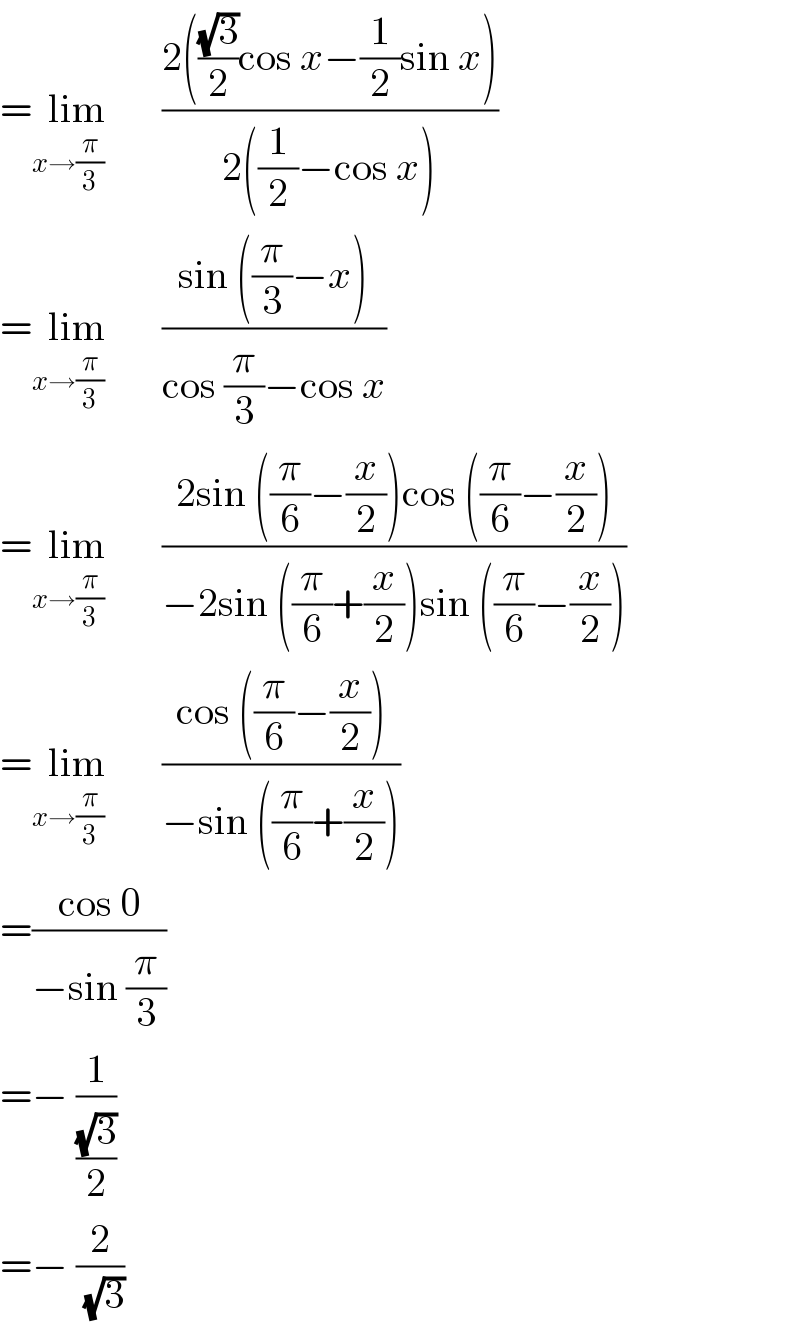
=lim_(x→(π/3) ) ((2(((√3)/2)cos x−(1/2)sin x))/(2((1/2)−cos x))) =lim_(x→(π/3) ) ((sin ((π/3)−x))/(cos (π/3)−cos x)) =lim_(x→(π/3) ) ((2sin ((π/6)−(x/2))cos ((π/6)−(x/2)))/(−2sin ((π/6)+(x/2))sin ((π/6)−(x/2)))) =lim_(x→(π/3) ) ((cos ((π/6)−(x/2)))/(−sin ((π/6)+(x/2)))) =((cos 0)/(−sin (π/3))) =− (1/((√3)/2)) =− (2/( (√3)))
$$=\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}\:\:\:\:\:} {\mathrm{lim}}\:\:\:\:\:\frac{\mathrm{2}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{cos}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{x}\right)}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{cos}\:{x}\right)}\: \\ $$$$=\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}\:\:\:\:\:} {\mathrm{lim}}\:\:\:\:\:\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−{x}\right)}{\mathrm{cos}\:\frac{\pi}{\mathrm{3}}−\mathrm{cos}\:{x}} \\ $$$$=\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}\:\:\:\:\:} {\mathrm{lim}}\:\:\:\:\:\frac{\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{6}}−\frac{{x}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}−\frac{{x}}{\mathrm{2}}\right)}{−\mathrm{2sin}\:\left(\frac{\pi}{\mathrm{6}}+\frac{{x}}{\mathrm{2}}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}−\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\underset{{x}\rightarrow\frac{\pi}{\mathrm{3}}\:\:\:\:\:} {\mathrm{lim}}\:\:\:\:\:\frac{\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}−\frac{{x}}{\mathrm{2}}\right)}{−\mathrm{sin}\:\left(\frac{\pi}{\mathrm{6}}+\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{cos}\:\mathrm{0}}{−\mathrm{sin}\:\frac{\pi}{\mathrm{3}}} \\ $$$$=−\:\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$=−\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *