Question Number 72894 by TawaTawa last updated on 04/Nov/19

Answered by mind is power last updated on 04/Nov/19
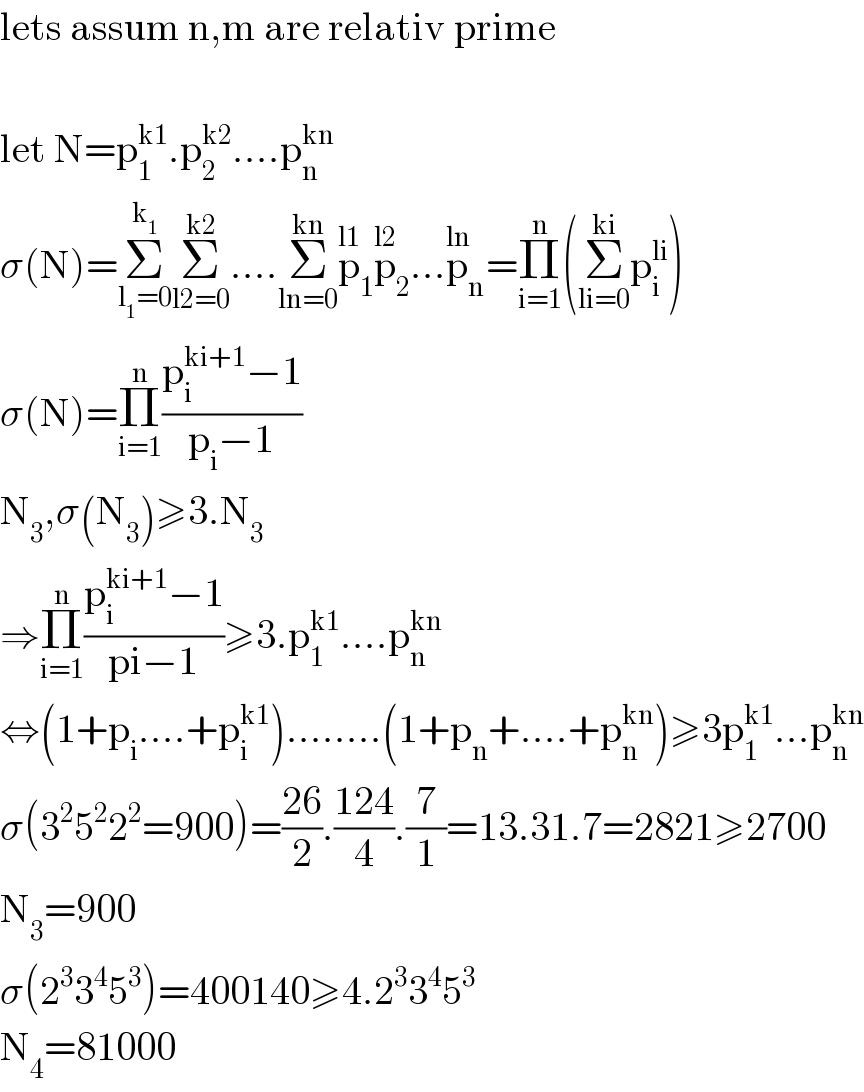
$$\mathrm{lets}\:\mathrm{assum}\:\mathrm{n},\mathrm{m}\:\mathrm{are}\:\mathrm{relativ}\:\mathrm{prime} \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{N}=\mathrm{p}_{\mathrm{1}} ^{\mathrm{k1}} .\mathrm{p}_{\mathrm{2}} ^{\mathrm{k2}} ….\mathrm{p}_{\mathrm{n}} ^{\mathrm{kn}} \\ $$$$\sigma\left(\mathrm{N}\right)=\underset{\mathrm{l}_{\mathrm{1}} =\mathrm{0}} {\overset{\mathrm{k}_{\mathrm{1}} } {\sum}}\underset{\mathrm{l2}=\mathrm{0}} {\overset{\mathrm{k2}} {\sum}}….\underset{\mathrm{ln}=\mathrm{0}} {\overset{\mathrm{kn}} {\sum}}\overset{\mathrm{l1}} {\mathrm{p}}_{\mathrm{1}} \overset{\mathrm{l2}} {\mathrm{p}}_{\mathrm{2}} …\overset{\mathrm{ln}} {\mathrm{p}}_{\mathrm{n}} =\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\underset{\mathrm{li}=\mathrm{0}} {\overset{\mathrm{ki}} {\sum}}\mathrm{p}_{\mathrm{i}} ^{\mathrm{li}} \right) \\ $$$$\sigma\left(\mathrm{N}\right)=\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\frac{\mathrm{p}_{\mathrm{i}} ^{\mathrm{ki}+\mathrm{1}} −\mathrm{1}}{\mathrm{p}_{\mathrm{i}} −\mathrm{1}} \\ $$$$\mathrm{N}_{\mathrm{3}} ,\sigma\left(\mathrm{N}_{\mathrm{3}} \right)\geqslant\mathrm{3}.\mathrm{N}_{\mathrm{3}} \\ $$$$\Rightarrow\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\frac{\mathrm{p}_{\mathrm{i}} ^{\mathrm{ki}+\mathrm{1}} −\mathrm{1}}{\mathrm{pi}−\mathrm{1}}\geqslant\mathrm{3}.\mathrm{p}_{\mathrm{1}} ^{\mathrm{k1}} ….\mathrm{p}_{\mathrm{n}} ^{\mathrm{kn}} \\ $$$$\Leftrightarrow\left(\mathrm{1}+\mathrm{p}_{\mathrm{i}} ….+\mathrm{p}_{\mathrm{i}} ^{\mathrm{k1}} \right)……..\left(\mathrm{1}+\mathrm{p}_{\mathrm{n}} +….+\mathrm{p}_{\mathrm{n}} ^{\mathrm{kn}} \right)\geqslant\mathrm{3p}_{\mathrm{1}} ^{\mathrm{k1}} …\mathrm{p}_{\mathrm{n}} ^{\mathrm{kn}} \\ $$$$\sigma\left(\mathrm{3}^{\mathrm{2}} \mathrm{5}^{\mathrm{2}} \mathrm{2}^{\mathrm{2}} =\mathrm{900}\right)=\frac{\mathrm{26}}{\mathrm{2}}.\frac{\mathrm{124}}{\mathrm{4}}.\frac{\mathrm{7}}{\mathrm{1}}=\mathrm{13}.\mathrm{31}.\mathrm{7}=\mathrm{2821}\geqslant\mathrm{2700} \\ $$$$\mathrm{N}_{\mathrm{3}} =\mathrm{900}\: \\ $$$$\sigma\left(\mathrm{2}^{\mathrm{3}} \mathrm{3}^{\mathrm{4}} \mathrm{5}^{\mathrm{3}} \right)=\mathrm{400140}\geqslant\mathrm{4}.\mathrm{2}^{\mathrm{3}} \mathrm{3}^{\mathrm{4}} \mathrm{5}^{\mathrm{3}} \\ $$$$\mathrm{N}_{\mathrm{4}} =\mathrm{81000} \\ $$
Commented by TawaTawa last updated on 04/Nov/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mind is power last updated on 04/Nov/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$$$ \\ $$
