Question-72930

Question Number 72930 by TawaTawa last updated on 05/Nov/19

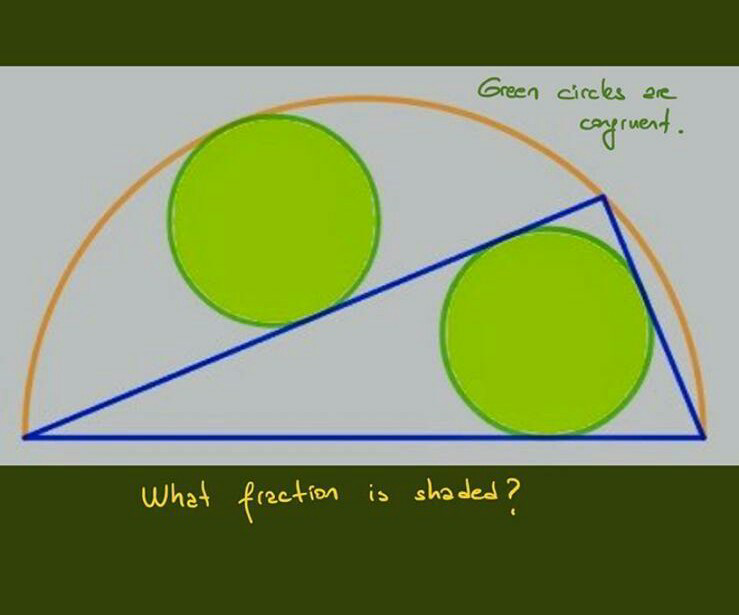
Answered by ajfour last updated on 05/Nov/19

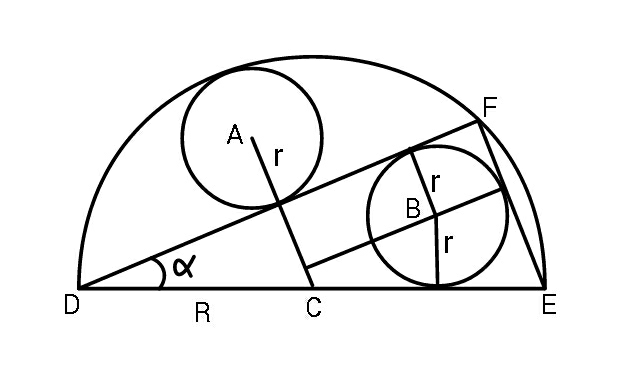
Commented by ajfour last updated on 05/Nov/19

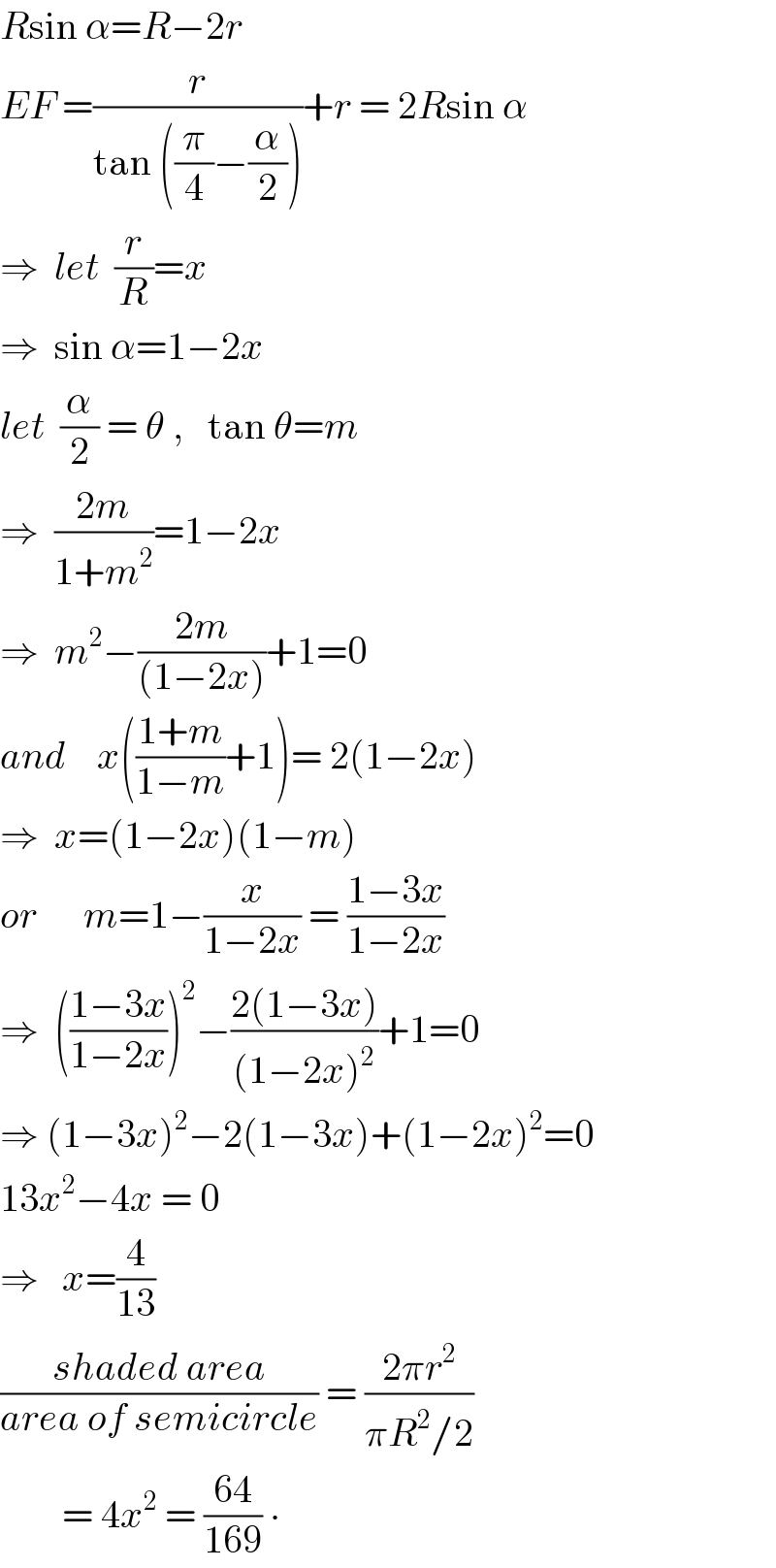
Rsin α=R−2r EF =(r/(tan ((π/4)−(α/2))))+r = 2Rsin α ⇒ let (r/R)=x ⇒ sin α=1−2x let (α/2) = θ , tan θ=m ⇒ ((2m)/(1+m^2 ))=1−2x ⇒ m^2 −((2m)/((1−2x)))+1=0 and x(((1+m)/(1−m))+1)= 2(1−2x) ⇒ x=(1−2x)(1−m) or m=1−(x/(1−2x)) = ((1−3x)/(1−2x)) ⇒ (((1−3x)/(1−2x)))^2 −((2(1−3x))/((1−2x)^2 ))+1=0 ⇒ (1−3x)^2 −2(1−3x)+(1−2x)^2 =0 13x^2 −4x = 0 ⇒ x=(4/(13)) ((shaded area)/(area of semicircle)) = ((2πr^2 )/(πR^2 /2)) = 4x^2 = ((64)/(169)) ∙

$${R}\mathrm{sin}\:\alpha={R}−\mathrm{2}{r} \\ $$$${EF}\:=\frac{{r}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\alpha}{\mathrm{2}}\right)}+{r}\:=\:\mathrm{2}{R}\mathrm{sin}\:\alpha \\ $$$$\Rightarrow\:\:{let}\:\:\frac{{r}}{{R}}={x} \\ $$$$\Rightarrow\:\:\mathrm{sin}\:\alpha=\mathrm{1}−\mathrm{2}{x}\: \\ $$$${let}\:\:\frac{\alpha}{\mathrm{2}}\:=\:\theta\:,\:\:\:\mathrm{tan}\:\theta={m} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{m}}{\mathrm{1}+{m}^{\mathrm{2}} }=\mathrm{1}−\mathrm{2}{x} \\ $$$$\Rightarrow\:\:{m}^{\mathrm{2}} −\frac{\mathrm{2}{m}}{\left(\mathrm{1}−\mathrm{2}{x}\right)}+\mathrm{1}=\mathrm{0} \\ $$$${and}\:\:\:\:{x}\left(\frac{\mathrm{1}+{m}}{\mathrm{1}−{m}}+\mathrm{1}\right)=\:\mathrm{2}\left(\mathrm{1}−\mathrm{2}{x}\right) \\ $$$$\Rightarrow\:\:{x}=\left(\mathrm{1}−\mathrm{2}{x}\right)\left(\mathrm{1}−{m}\right) \\ $$$${or}\:\:\:\:\:\:{m}=\mathrm{1}−\frac{{x}}{\mathrm{1}−\mathrm{2}{x}}\:=\:\frac{\mathrm{1}−\mathrm{3}{x}}{\mathrm{1}−\mathrm{2}{x}} \\ $$$$\Rightarrow\:\:\left(\frac{\mathrm{1}−\mathrm{3}{x}}{\mathrm{1}−\mathrm{2}{x}}\right)^{\mathrm{2}} −\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{3}{x}\right)}{\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{2}} }+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{1}−\mathrm{3}{x}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}−\mathrm{3}{x}\right)+\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{13}{x}^{\mathrm{2}} −\mathrm{4}{x}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:{x}=\frac{\mathrm{4}}{\mathrm{13}}\: \\ $$$$\frac{{shaded}\:{area}}{{area}\:{of}\:{semicircle}}\:=\:\frac{\mathrm{2}\pi{r}^{\mathrm{2}} }{\pi{R}^{\mathrm{2}} /\mathrm{2}}\: \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{4}{x}^{\mathrm{2}} \:=\:\frac{\mathrm{64}}{\mathrm{169}}\:\centerdot \\ $$

Commented by TawaTawa last updated on 05/Nov/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply