Question Number 73037 by aliesam last updated on 05/Nov/19
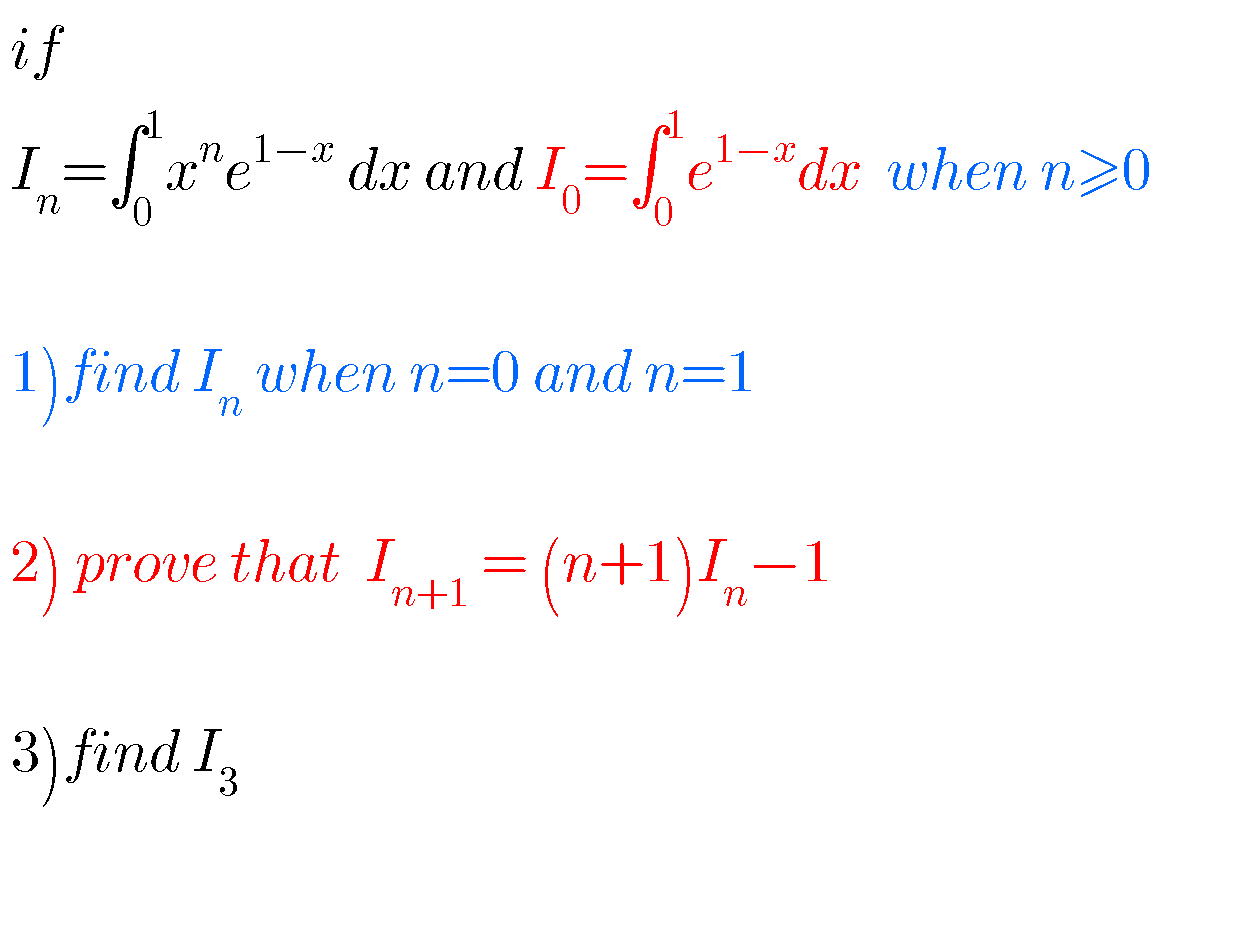
Commented by mathmax by abdo last updated on 06/Nov/19
![1) I_0 =∫_0 ^1 e^(1−x) dx =[−e^(1−x) ]_0 ^1 =e−1 I_1 =∫_0 ^1 x e^(1−x) dx =_(by parts) [−xe^(1−x) ]_0 ^1 −∫_0 ^1 (−e^(1−x) )dx =−1+e−1 =e−2 2) I_(n+1) =∫_0 ^1 x^(n+1) e^(1−x) dx =e ∫_0 ^1 x^(n+1) e^(−x) dx by parts u=x^(n+1) and v^, =e^(−x) ⇒∫_0 ^1 x^(n+1) e^(−x ) dx =[−x^(n+1) e^(−x) ]_0 ^1 −∫_0 ^1 (n+1)x^n (−e^(−x) )dx =−e^(−1) +(n+1) ∫_0 ^1 x^n e^(−x) dx ⇒I_(n+1) =e(−e^(−1) +(n+1)∫_0 ^1 x^n e^(−x) dx) =−1+(n+1)∫_0 ^1 x^n e^(1−x) dx =(n+1)I_n −1 ⇒ I_(n+1) =(n+1)I_n −1 remrk we have I_n =nI_(n−1) −1 for n≥1 let V_n =(I_n /(n!)) ⇒V_(n+1) =(I_(n+1) /((n+1)!)) =(((n+1)I_n )/((n+1)!)) −1 =(I_n /(n!))−1 =V_n −1 ⇒V_(n+1) −V_n =−1 ⇒Σ_(k=0) ^(n−1) (V_(k+1) −V_k )=−n ⇒ V_n −V_0 =−n ⇒V_n =V_0 −n =e−1−n ⇒(I_n /(n!)) =e−1−n ⇒ I_n =n!{e−1−n}](https://www.tinkutara.com/question/Q73082.png)
$$\left.\mathrm{1}\right)\:{I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{\mathrm{1}−{x}} {dx}\:=\left[−{e}^{\mathrm{1}−{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} ={e}−\mathrm{1} \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} {x}\:{e}^{\mathrm{1}−{x}} \:{dx}\:=_{{by}\:{parts}} \:\:\left[−{xe}^{\mathrm{1}−{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left(−{e}^{\mathrm{1}−{x}} \right){dx} \\ $$$$=−\mathrm{1}+{e}−\mathrm{1}\:={e}−\mathrm{2} \\ $$$$\left.\mathrm{2}\right)\:{I}_{{n}+\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}+\mathrm{1}} \:{e}^{\mathrm{1}−{x}} {dx}\:={e}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}+\mathrm{1}} \:{e}^{−{x}} \:{dx}\:{by}\:{parts}\:{u}={x}^{{n}+\mathrm{1}} \:{and} \\ $$$${v}^{,} ={e}^{−{x}} \:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}+\mathrm{1}} \:{e}^{−{x}\:} {dx}\:=\left[−{x}^{{n}+\mathrm{1}} {e}^{−{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({n}+\mathrm{1}\right){x}^{{n}} \left(−{e}^{−{x}} \right){dx} \\ $$$$=−{e}^{−\mathrm{1}} \:+\left({n}+\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:{e}^{−{x}} \:{dx}\:\Rightarrow{I}_{{n}+\mathrm{1}} ={e}\left(−{e}^{−\mathrm{1}} \:+\left({n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:{e}^{−{x}} {dx}\right) \\ $$$$=−\mathrm{1}+\left({n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:{e}^{\mathrm{1}−{x}} {dx}\:=\left({n}+\mathrm{1}\right){I}_{{n}} −\mathrm{1}\:\Rightarrow \\ $$$${I}_{{n}+\mathrm{1}} =\left({n}+\mathrm{1}\right){I}_{{n}} −\mathrm{1}\:\:\: \\ $$$${remrk}\:\:\:{we}\:{have}\:{I}_{{n}} ={nI}_{{n}−\mathrm{1}} −\mathrm{1}\:\:{for}\:{n}\geqslant\mathrm{1}\:\:{let} \\ $$$${V}_{{n}} =\frac{{I}_{{n}} }{{n}!}\:\Rightarrow{V}_{{n}+\mathrm{1}} =\frac{{I}_{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}\:=\frac{\left({n}+\mathrm{1}\right){I}_{{n}} }{\left({n}+\mathrm{1}\right)!}\:−\mathrm{1} \\ $$$$=\frac{{I}_{{n}} }{{n}!}−\mathrm{1}\:={V}_{{n}} −\mathrm{1}\:\Rightarrow{V}_{{n}+\mathrm{1}} −{V}_{{n}} =−\mathrm{1}\:\Rightarrow\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left({V}_{{k}+\mathrm{1}} −{V}_{{k}} \right)=−{n}\:\Rightarrow \\ $$$${V}_{{n}} −{V}_{\mathrm{0}} =−{n}\:\Rightarrow{V}_{{n}} ={V}_{\mathrm{0}} −{n}\:={e}−\mathrm{1}−{n}\:\Rightarrow\frac{{I}_{{n}} }{{n}!}\:={e}−\mathrm{1}−{n}\:\Rightarrow \\ $$$${I}_{{n}} ={n}!\left\{{e}−\mathrm{1}−{n}\right\} \\ $$
Answered by mind is power last updated on 05/Nov/19
![I_0 =∫_0 ^1 e^(1−x) dx=[−e^(1−x) ]_0 ^1 =e−1 I_1 =∫_0 ^1 xe^(1−x) dx=[−xe^(1−x) ]_0 ^1 +∫e^(1−x) dx =−1+e−1=e−2 I_(n+1) =∫_0 ^1 x^(n+1) e^(1−x) =[−x^(n+1) e^(1−x) ]_0 ^1 +(n+1)∫_0 ^1 x^n e^(1−x) dx integration by part =−1+(n+1)∫_0 ^1 x^n e^(1−x) dx=−1+(n+1)I_n I_3 =3I_2 −1 I_2 =2I_1 −1=2(e−2)−1=2e−5 I_3 =3(2e−5)−1=6e−16](https://www.tinkutara.com/question/Q73076.png)
$$\mathrm{I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{e}^{\mathrm{1}−\mathrm{x}} \mathrm{dx}=\left[−\mathrm{e}^{\mathrm{1}−\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{e}−\mathrm{1} \\ $$$$\mathrm{I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xe}^{\mathrm{1}−\mathrm{x}} \mathrm{dx}=\left[−\mathrm{xe}^{\mathrm{1}−\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} +\int\mathrm{e}^{\mathrm{1}−\mathrm{x}} \mathrm{dx} \\ $$$$=−\mathrm{1}+\mathrm{e}−\mathrm{1}=\mathrm{e}−\mathrm{2} \\ $$$$\mathrm{I}_{\mathrm{n}+\mathrm{1}} =\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}+\mathrm{1}} \mathrm{e}^{\mathrm{1}−\mathrm{x}} =\left[−\mathrm{x}^{\mathrm{n}+\mathrm{1}} \mathrm{e}^{\mathrm{1}−\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{1}} +\left(\mathrm{n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}} \mathrm{e}^{\mathrm{1}−\mathrm{x}} \mathrm{dx}\:\:\mathrm{integration}\:\mathrm{by}\:\mathrm{part} \\ $$$$=−\mathrm{1}+\left(\mathrm{n}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{n}} \mathrm{e}^{\mathrm{1}−\mathrm{x}} \mathrm{dx}=−\mathrm{1}+\left(\mathrm{n}+\mathrm{1}\right)\mathrm{I}_{\mathrm{n}} \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{3I}_{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{I}_{\mathrm{2}} =\mathrm{2I}_{\mathrm{1}} −\mathrm{1}=\mathrm{2}\left(\mathrm{e}−\mathrm{2}\right)−\mathrm{1}=\mathrm{2e}−\mathrm{5} \\ $$$$\mathrm{I}_{\mathrm{3}} =\mathrm{3}\left(\mathrm{2e}−\mathrm{5}\right)−\mathrm{1}=\mathrm{6e}−\mathrm{16} \\ $$
