Question Number 73113 by TawaTawa last updated on 06/Nov/19
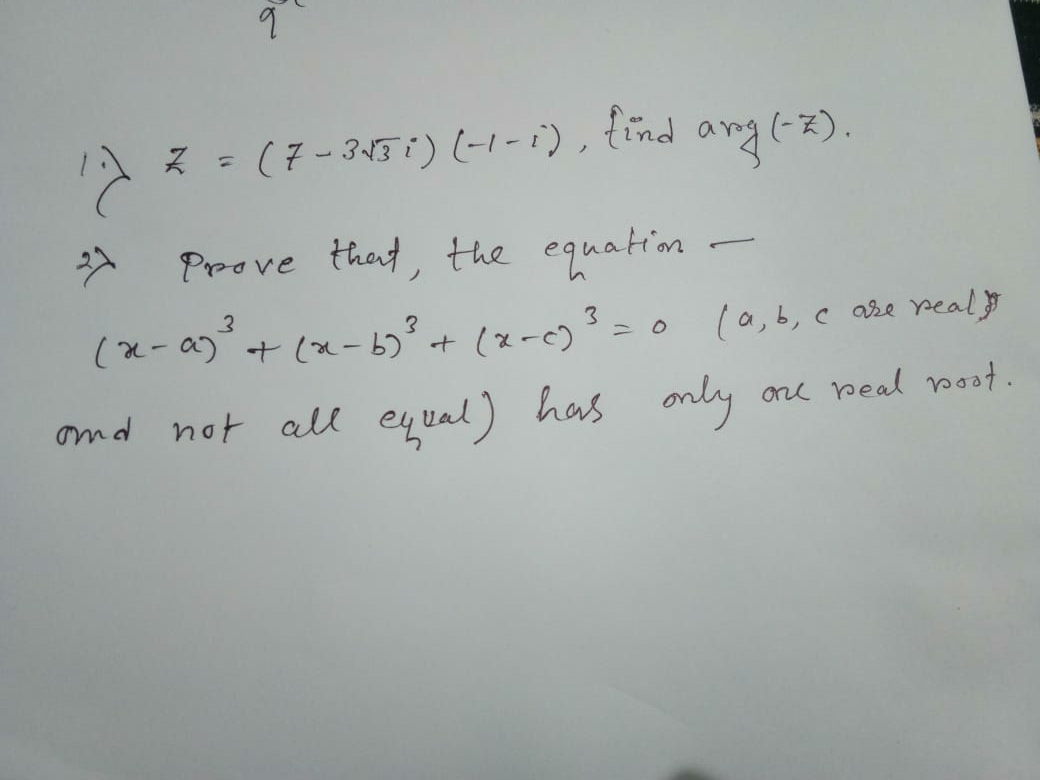
Commented by mathmax by abdo last updated on 06/Nov/19
![1) we have arg(z)=arg(7−3(√3)i)+arg(−1−i)[2π] ∣7−3(√3)∣ =(√(49+27))=(√(76)) ⇒7−3(√3)=(√(76))e^(iarctan(((−3(√3))/7))) ⇒ arg(7−3(√3)) =−arctan(((3(√3))/7)) −1−i =(√2)(−(1/( (√2)))−(i/( (√2)))) =(√2)e^(i((5π)/4)) ⇒arg(z)=((5π)/4) −arctan(((3(√3))/7))[2π]](https://www.tinkutara.com/question/Q73118.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{arg}\left({z}\right)={arg}\left(\mathrm{7}−\mathrm{3}\sqrt{\mathrm{3}}{i}\right)+{arg}\left(−\mathrm{1}−{i}\right)\left[\mathrm{2}\pi\right] \\ $$$$\mid\mathrm{7}−\mathrm{3}\sqrt{\mathrm{3}}\mid\:=\sqrt{\mathrm{49}+\mathrm{27}}=\sqrt{\mathrm{76}}\:\Rightarrow\mathrm{7}−\mathrm{3}\sqrt{\mathrm{3}}=\sqrt{\mathrm{76}}{e}^{{iarctan}\left(\frac{−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{7}}\right)} \:\Rightarrow \\ $$$${arg}\left(\mathrm{7}−\mathrm{3}\sqrt{\mathrm{3}}\right)\:=−{arctan}\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{7}}\right) \\ $$$$−\mathrm{1}−{i}\:=\sqrt{\mathrm{2}}\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\:=\sqrt{\mathrm{2}}{e}^{{i}\frac{\mathrm{5}\pi}{\mathrm{4}}} \:\Rightarrow{arg}\left({z}\right)=\frac{\mathrm{5}\pi}{\mathrm{4}}\:−{arctan}\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{7}}\right)\left[\mathrm{2}\pi\right] \\ $$$$ \\ $$
Commented by TawaTawa last updated on 06/Nov/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 06/Nov/19
$${you}\:{are}\:{welcome}. \\ $$
Answered by mr W last updated on 06/Nov/19
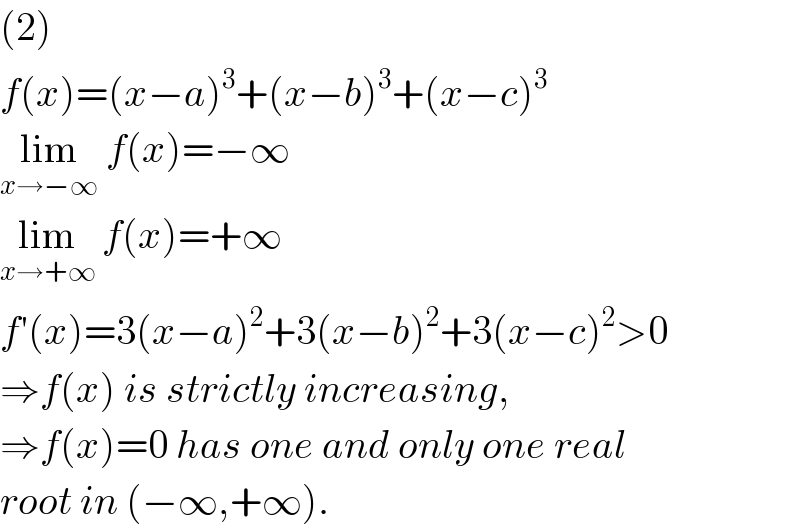
$$\left(\mathrm{2}\right) \\ $$$${f}\left({x}\right)=\left({x}−{a}\right)^{\mathrm{3}} +\left({x}−{b}\right)^{\mathrm{3}} +\left({x}−{c}\right)^{\mathrm{3}} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{f}\left({x}\right)=−\infty \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:{f}\left({x}\right)=+\infty \\ $$$${f}'\left({x}\right)=\mathrm{3}\left({x}−{a}\right)^{\mathrm{2}} +\mathrm{3}\left({x}−{b}\right)^{\mathrm{2}} +\mathrm{3}\left({x}−{c}\right)^{\mathrm{2}} >\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)\:{is}\:{strictly}\:{increasing}, \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{0}\:{has}\:{one}\:{and}\:{only}\:{one}\:{real} \\ $$$${root}\:{in}\:\left(−\infty,+\infty\right). \\ $$
Commented by TawaTawa last updated on 06/Nov/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
