Question-73117

Question Number 73117 by aliesam last updated on 06/Nov/19

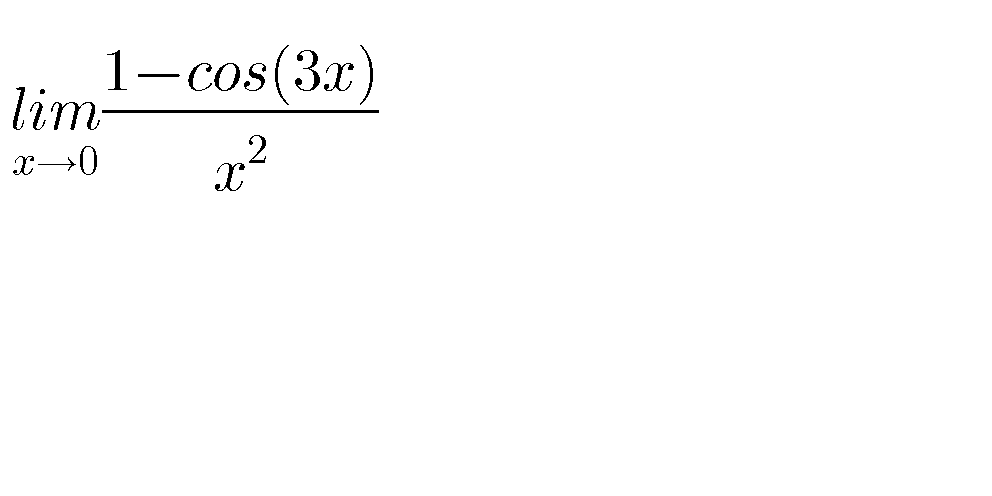
Commented by mathmax by abdo last updated on 06/Nov/19

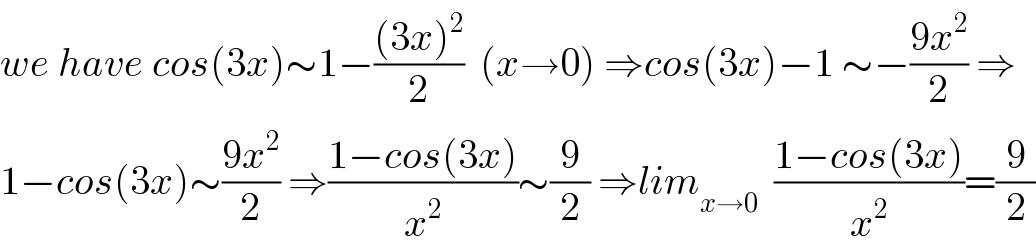
we have cos(3x)∼1−(((3x)^2 )/2) (x→0) ⇒cos(3x)−1 ∼−((9x^2 )/2) ⇒ 1−cos(3x)∼((9x^2 )/2) ⇒((1−cos(3x))/x^2 )∼(9/2) ⇒lim_(x→0) ((1−cos(3x))/x^2 )=(9/2)

$${we}\:{have}\:{cos}\left(\mathrm{3}{x}\right)\sim\mathrm{1}−\frac{\left(\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow{cos}\left(\mathrm{3}{x}\right)−\mathrm{1}\:\sim−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{1}−{cos}\left(\mathrm{3}{x}\right)\sim\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow\frac{\mathrm{1}−{cos}\left(\mathrm{3}{x}\right)}{{x}^{\mathrm{2}} }\sim\frac{\mathrm{9}}{\mathrm{2}}\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}−{cos}\left(\mathrm{3}{x}\right)}{{x}^{\mathrm{2}} }=\frac{\mathrm{9}}{\mathrm{2}} \\ $$

Answered by mind is power last updated on 06/Nov/19

cos(3x)=4cos^3 (x)−3cos(x) 1−cos(3x)=−4cos^3 (x)+3cos(x)+1=−4(cos(x)−1)(cos^2 (x)+cos(x)+(1/4)) =−4(−2sin^2 ((x/2)))(cos^2 (x)+cos(x)+(1/4)) ((1−cos(3x))/x^2 )=((8sin^2 ((x/2)))/(4((x/2))^2 )).(cos^2 (x)+cos(x)+(1/4)) =2.(((sin((x/2)))/(x/2)))^2 .(cos^2 (x)+cos(x)+(1/4)) lim_(x→0) ((sin(x))/x)=1 ⇒=2.1^2 .(1+1+(1/4))=(9/2)

$$\mathrm{cos}\left(\mathrm{3x}\right)=\mathrm{4cos}^{\mathrm{3}} \left(\mathrm{x}\right)−\mathrm{3cos}\left(\mathrm{x}\right) \\ $$$$\mathrm{1}−\mathrm{cos}\left(\mathrm{3x}\right)=−\mathrm{4cos}^{\mathrm{3}} \left(\mathrm{x}\right)+\mathrm{3cos}\left(\mathrm{x}\right)+\mathrm{1}=−\mathrm{4}\left(\mathrm{cos}\left(\mathrm{x}\right)−\mathrm{1}\right)\left(\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{cos}\left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=−\mathrm{4}\left(−\mathrm{2sin}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\left(\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{cos}\left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{3x}\right)}{\mathrm{x}^{\mathrm{2}} }=\frac{\mathrm{8sin}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\mathrm{4}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} }.\left(\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{cos}\left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\mathrm{2}.\left(\frac{\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)}{\frac{\mathrm{x}}{\mathrm{2}}}\right)^{\mathrm{2}} .\left(\mathrm{cos}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{cos}\left(\mathrm{x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{x}}=\mathrm{1} \\ $$$$\Rightarrow=\mathrm{2}.\mathrm{1}^{\mathrm{2}} .\left(\mathrm{1}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\right)=\frac{\mathrm{9}}{\mathrm{2}} \\ $$

Answered by malwaan last updated on 07/Nov/19

lim_(x→0) (([1−cos(3x)]×[1+cos(3x)])/(x^2 ×[1+cos(3x)])) =lim_(x→0) ((sin^2 (3x))/(x^2 [1+cos(3x)]))=(3^2 /(1+1))=(9/2)

$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\frac{\left[\mathrm{1}−\boldsymbol{{cos}}\left(\mathrm{3}\boldsymbol{{x}}\right)\right]×\left[\mathrm{1}+\boldsymbol{{cos}}\left(\mathrm{3}\boldsymbol{{x}}\right)\right]}{\boldsymbol{{x}}^{\mathrm{2}} ×\left[\mathrm{1}+\boldsymbol{{cos}}\left(\mathrm{3}\boldsymbol{{x}}\right)\right]} \\ $$$$=\underset{\boldsymbol{{x}}\rightarrow\mathrm{0}} {\boldsymbol{{lim}}}\frac{\boldsymbol{{sin}}^{\mathrm{2}} \left(\mathrm{3}\boldsymbol{{x}}\right)}{\boldsymbol{{x}}^{\mathrm{2}} \left[\mathrm{1}+\boldsymbol{{cos}}\left(\mathrm{3}\boldsymbol{{x}}\right)\right]}=\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{1}+\mathrm{1}}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply