Question-7314

Question Number 7314 by Rasheed Soomro last updated on 23/Aug/16

Commented by Rasheed Soomro last updated on 23/Aug/16

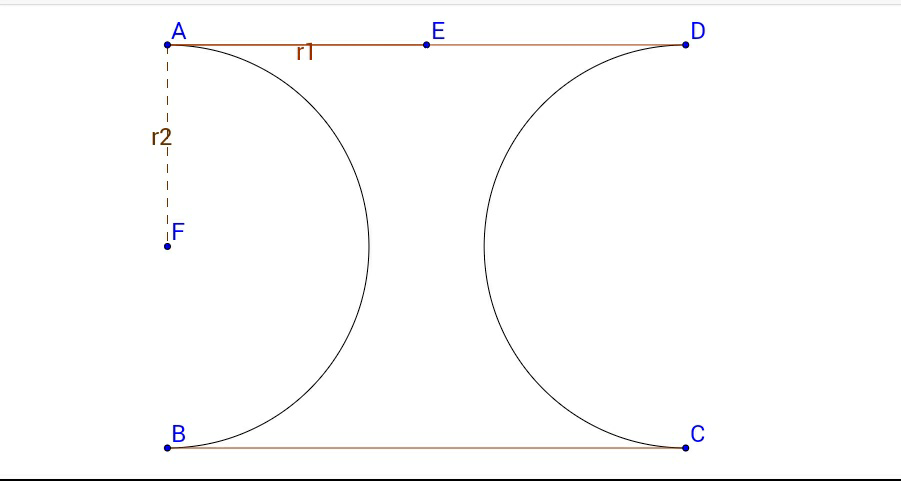
T o p a n d b o t t o m o f a s o l i d a r e c o n g r u e n t c i r c l e s .

A b o v e i s t h e c r o s s - s e c t i o n o f t h e s o l i d, w h i c h

i s o b t a i n e d b y c u t t i n g t h e s o l i d i n t w o e q u a l p a r t s .

F i n d o u t t h e v o l u m e o f t h e s o l i d .

Answered by Yozzia last updated on 24/Aug/16

D e f i n e t h e c i r c l e w w i t h c a r t e s i a n

e q u a t i o n x^{2} + {(y - r_{1})}^{2} = r_{2}^{2} w h e r e r_{1} > r_{2} > 0 .

\Rightarrow y = r_{1} \pm \sqrt{r_{2}^{2} - x^{2}} {∣ x ∣⩽ r_{2}} .

T h e p r o b l e m g i v e n c a n b e v i e w e d a s f i n d i n g

t h e v o l u m e V o f t h e f i g u r e g e n e r a t e d

w h e n a p a r t o f w, w h o s e y c o o r d i n a t e s

s a t i s f y 0 < y ⩽ r_{1}, i s r o t a t e d 2 π r a d i a n s

a b o u t t h e x - a x i s .

∴ y = r_{1} - \sqrt{r_{2}^{2} - x^{2}} {∣ x ∣⩽ r_{2}} .

U s i n g V = π \int_{- r_{2}}^{r_{2}} y^{2} d x w e g e t

V = 2 π \int_{0}^{r_{2}} {(r_{1} - \sqrt{r_{2}^{2} - x^{2}})}^{2} d x {y^{2} i s e v e n} .

V = 2 π \int_{0}^{r_{2}} {r_{1}^{2} + r_{2}^{2} - x^{2} - 2 r_{1} \sqrt{r_{2}^{2} - x^{2}}} d x

L e t x = r_{2} s i n θ 0 ⩽ θ ⩽ 2 π . \Rightarrow d x = r_{2} c o s θ d θ .

A t x = 0, θ = 0 a n d a t x = r_{2}, θ = \frac{π}{2} .

∴ V = 2 π r_{2} \int_{0}^{π / 2} {r_{1}^{2} + r_{2}^{2} - r_{2}^{2} {s i n}^{2} θ - 2 r_{1} \sqrt{r_{2}^{2} - r_{2}^{2} {s i n}^{2} θ}} c o s θ d θ

V = 2 π r_{2} [\int_{0}^{π / 2} (r_{1}^{2} + r_{2}^{2}) c o s θ d θ - r_{2}^{2} \int_{0}^{π / 2} {s i n}^{2} θ c o s θ d θ - 2 r_{1} r_{2} \int_{0}^{π / 2} {c o s}^{2} θ d θ]

V = 2 π r_{2} [r_{1}^{2} + r_{2}^{2} - {\frac{r_{2}^{2} u^{3}}{3}}_{0}^{1} - r_{1} r_{2} \int_{0}^{π / 2} (1 + c o s 2 θ) d θ]

V = 2 π r_{2} [r_{1}^{2} + r_{2}^{2} - \frac{r_{2}^{2}}{3} - r_{1} r_{2} {θ + \frac{1}{2} s i n 2 θ}_{0}^{π / 2}]

V = 2 π r_{2} [r_{1}^{2} + \frac{2}{3} r_{2}^{2} - \frac{r_{1} r_{2} π}{2}]

V = \frac{π r_{2}}{3} [6 r_{1}^{2} + 4 r_{2}^{2} - 3 π r_{1} r_{2}]

V = \frac{2 π r_{2}}{3} (3 r_{1}^{2} + 2 r_{2}^{2}) - π^{2} r_{1} r_{2}^{2}

V = 2 π r_{1}^{2} r_{2} + \frac{4 π r_{2}^{3}}{3} - π^{2} r_{2}^{2} r_{1}

- - - - - - - - - - - - - - - - - - - - - - - - - -

B y P a p p u s - G u l d i n t h e o r e m,

V = 2 π A \bar{y}

w h e r e A = a r e a b o u n d e d b e t w e e n

y = r_{1} - \sqrt{r_{2}^{2} - x^{2}}, l i n e s y = 0, x = \pm r_{2}

a n d \bar{y} = d i s t a n c e o f c e n t r o i d o f A f r o m

a x i s o f r o t a t i o n (y = 0) .

∴ \bar{y} = \frac{V}{2 π A} .

I t c a n b e s h o w n t h a t A = \frac{r_{2} (4 r_{1} - π r_{2})}{2} .

∴ \bar{y} = \frac{\frac{π r_{2}}{3} (6 r_{1}^{2} + 4 r_{2}^{2} - 3 π r_{1} r_{2})}{2 π \frac{r_{2} (4 r_{1} - π r_{2})}{2}}

o r \bar{y} = \frac{6 r_{1}^{2} + 4 r_{2}^{2} - 3 π r_{1} r_{2}}{3 (4 r_{1} - π r_{2})}

Commented by Rasheed Soomro last updated on 24/Aug/16

THANKS! I a m t r y i n g t o u n d e r s t a n d . A t t h e m o m e n t

I a m n o t m u c h i n v o l v e d i n a n a l y t i c a p p r o a c h .

Commented by Yozzia last updated on 24/Aug/16

Commented by Yozzia last updated on 24/Aug/16

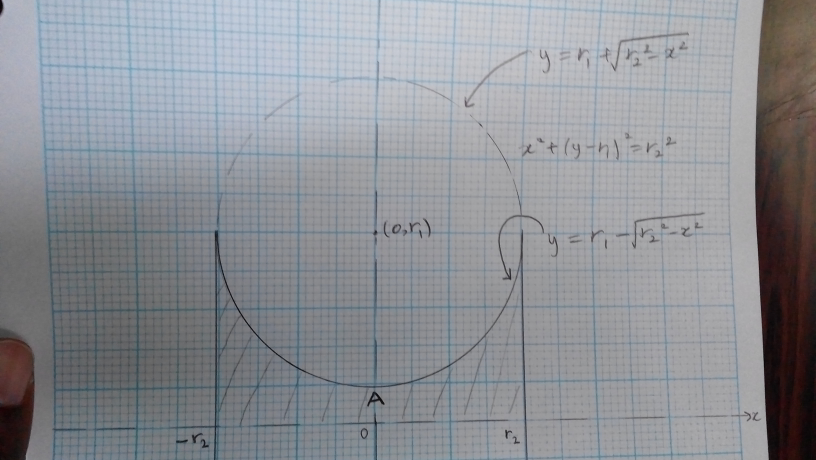
T h e v o l u m e y o u s e e k c a n b e f o u n d

b y r o t a t i n g t h e l o w e r s e c t i o n o f t h e

c i r c l e x^{2} + {(y - r_{1})}^{2} = r_{2}^{2} 360 ° a b o u t

t h e x - a x i s . I h a v e u s e d f u l l i n k t o

s h o w t h e l o w e r s e c t i o n a n d t h e u p p e r

s e c t i o n i s i n b r o k e n i n k .

Commented by Rasheed Soomro last updated on 24/Aug/16

TH α n k S A g a i n! T h e g r a p h a n d t h e c o m m e n t

i s g r e a t h e l p i n u n d e r s t a n d i n g y o u r a n s w e r!

I h a d a n o t h e r i d e a :

V o l u m e o f c y l i n d e r - s e m i - c i r c l e g a p e a r o u n d

S e m i - c i r c l e g a p e = \frac{π r_{2}^{2}}{2} \times c i r c u m f e r e n c e .

I w a s i n c o n f u s i o n w h i c h c i r c l e - c i r c u m f e r e n c e

s h o u l d b e u s e d . C i r c l e w i t h r a d i u s r_{1} o r c i r c l e

w i t h r a d i u s r_{1} - r_{2} o r a v e r a g e o f t h e b o t h .

P e r h a p s I a m n o t s u c c e s s f u l t o c l e a r m y i d e a .

Commented by Yozzia last updated on 24/Aug/16

- - - - - - - - - - - - - - - - - - - - - - - - -

C e n t r o i d o f s e m i c i r c u l a r a r e a i s \frac{4 r_{2}}{3 π} f r o m t h e c e n t e r o f s t r a i g h t e d g e .

∴ R e q u i r e d d i s t a n c e = (r_{1} - r_{2}) + (r_{2} - \frac{4 r_{2}}{3 π}) = r_{1} - \frac{4 r_{2}}{3 π}

C i r c u m f e r e n c e = 2 π (r_{1} - \frac{4 r_{2}}{3 π}) = 2 π r_{1} - \frac{8 r_{2}}{3} = c

v o l u m e = \frac{π r_{2}^{2}}{2} (2 π r_{1} - \frac{8 r_{2}}{3}) = π^{2} r_{1} r_{2}^{2} - \frac{4 π r_{2}^{3}}{3}

\Rightarrow R e q u i r e d v o l u m e = 2 π r_{1}^{2} r_{2} - c = 2 π r_{1}^{2} r_{2} + \frac{4 π r_{2}^{3}}{3} - π^{2} r_{1} r_{2}^{2} a s w a s f o u n d .

Facebook Tweet Pin