Menu Close

Question-73210

Tinku Tara 0 Comments
Pin




Question Number 73210 by TawaTawa last updated on 08/Nov/19
Commented by mr W last updated on 09/Nov/19
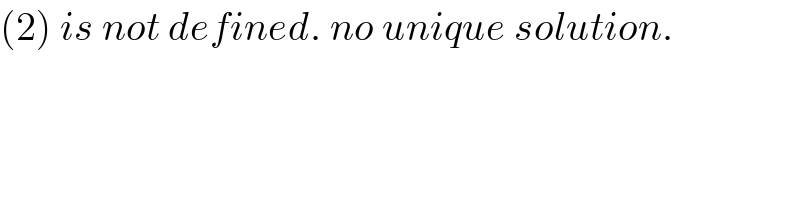
(2) is not defined. no unique solution.
$$\left(\mathrm{2}\right)\:{is}\:{not}\:{defined}.\:{no}\:{unique}\:{solution}. \\ $$
Commented by TawaTawa last updated on 09/Nov/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mind is power last updated on 08/Nov/19
let A=center of m_1 let B=center of m_2 AB=0.8m CM of(m_1 ,m_2 )=D such that m_1 .AD=m_2 DB⇒DB=((15)/(25))AD AD+DB=0.8⇒AD=0.5m 2) let G=center of Rod wich is midpoint since the road is uniform R.road =h=0CM of (m_1 ,R,m_2 )=CM(CM(m_1 ,m_2 ),R(15)) CM(m1,m2)=D(M=40) DR=0.5−0.4=0.1 ⇒Dh.40=15.hR⇒hR=((40)/(15))=(8/3)Dh Dh+hR=DR=0.1⇒Dh=((0.3)/(11)) ⇒Ah=((0.3)/(11))+0.5=((5.8)/(11))=0.527..m 2) let A point (0,h) let B(0,t)⇒∣t−h∣=l C(h,0) h^2 +t^2 =l^2 his representation in coordinat plan of our problem C,2m,Aand B mass=m find G suche mGA^→ +mGB^→ +2mGC^→ =0 ′vector′ ⇒(4m)GA^→ =−mAB^→ −2mAC^→ ⇒GA^→ =((−AB^→ )/4)−2((AC^→ )/4) AB^→ =(0.t−h)=(0,l) AC^→ =(h,−h) GA^→ =(−(h/2),−l+(h/2)) ⇒AG^→ =((h/2),l−(h/2)) G(x,y)⇒ { ((x=(h/2))),((y−h=l−(h/2)⇒y=l+(h/2))) :} we can go forther in case CB=l ⇒(h^2 +t^2 )=l^2 =∣h−t∣^2 =h^2 +t^2 −2ht⇒ht=0 CA=l⇒2h^2 =l^2 ⇒h=+_− (l/( (√2))) we have 4 case if we want
$$\mathrm{let}\:\mathrm{A}=\mathrm{center}\:\mathrm{of}\:\mathrm{m}_{\mathrm{1}} \\ $$$$\mathrm{let}\:\mathrm{B}=\mathrm{center}\:\mathrm{of}\:\mathrm{m}_{\mathrm{2}} \\ $$$$\mathrm{AB}=\mathrm{0}.\mathrm{8m} \\ $$$$\mathrm{CM}\:\mathrm{of}\left(\mathrm{m}_{\mathrm{1}} ,\mathrm{m}_{\mathrm{2}} \right)=\mathrm{D} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{m}_{\mathrm{1}} .\mathrm{AD}=\mathrm{m}_{\mathrm{2}} \mathrm{DB}\Rightarrow\mathrm{DB}=\frac{\mathrm{15}}{\mathrm{25}}\mathrm{AD} \\ $$$$\mathrm{AD}+\mathrm{DB}=\mathrm{0}.\mathrm{8}\Rightarrow\mathrm{AD}=\mathrm{0}.\mathrm{5m} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{G}=\mathrm{center}\:\mathrm{of}\:\mathrm{Rod}\:\mathrm{wich}\:\mathrm{is}\:\mathrm{midpoint}\:\mathrm{since}\:\mathrm{the}\:\mathrm{road}\:\mathrm{is}\:\mathrm{uniform} \\ $$$$\mathrm{R}.\mathrm{road} \\ $$$$=\mathrm{h}=\mathrm{0CM}\:\mathrm{of}\:\left(\mathrm{m}_{\mathrm{1}} ,\mathrm{R},\mathrm{m}_{\mathrm{2}} \right)=\mathrm{CM}\left(\mathrm{CM}\left(\mathrm{m}_{\mathrm{1}} ,\mathrm{m}_{\mathrm{2}} \right),\mathrm{R}\left(\mathrm{15}\right)\right) \\ $$$$\mathrm{CM}\left(\mathrm{m1},\mathrm{m2}\right)=\mathrm{D}\left(\mathrm{M}=\mathrm{40}\right) \\ $$$$\mathrm{DR}=\mathrm{0}.\mathrm{5}−\mathrm{0}.\mathrm{4}=\mathrm{0}.\mathrm{1} \\ $$$$\Rightarrow\mathrm{Dh}.\mathrm{40}=\mathrm{15}.\mathrm{hR}\Rightarrow\mathrm{hR}=\frac{\mathrm{40}}{\mathrm{15}}=\frac{\mathrm{8}}{\mathrm{3}}\mathrm{Dh} \\ $$$$\mathrm{Dh}+\mathrm{hR}=\mathrm{DR}=\mathrm{0}.\mathrm{1}\Rightarrow\mathrm{Dh}=\frac{\mathrm{0}.\mathrm{3}}{\mathrm{11}} \\ $$$$\Rightarrow\mathrm{Ah}=\frac{\mathrm{0}.\mathrm{3}}{\mathrm{11}}+\mathrm{0}.\mathrm{5}=\frac{\mathrm{5}.\mathrm{8}}{\mathrm{11}}=\mathrm{0}.\mathrm{527}..\mathrm{m} \\ $$$$\left.\mathrm{2}\right) \\ $$$$\mathrm{let}\:\mathrm{A}\:\mathrm{point}\:\left(\mathrm{0},\mathrm{h}\right) \\ $$$$\mathrm{let}\:\mathrm{B}\left(\mathrm{0},\mathrm{t}\right)\Rightarrow\mid\mathrm{t}−\mathrm{h}\mid=\mathrm{l} \\ $$$$\mathrm{C}\left(\mathrm{h},\mathrm{0}\right)\:\:\mathrm{h}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} =\mathrm{l}^{\mathrm{2}} \\ $$$$\mathrm{his}\:\mathrm{representation}\:\mathrm{in}\:\mathrm{coordinat}\:\mathrm{plan}\:\mathrm{of}\:\mathrm{our}\:\mathrm{problem} \\ $$$$\mathrm{C},\mathrm{2m},\mathrm{Aand}\:\mathrm{B}\:\mathrm{mass}=\mathrm{m} \\ $$$$\mathrm{find}\:\mathrm{G}\:\mathrm{suche}\: \\ $$$$\mathrm{mG}\overset{\rightarrow} {\mathrm{A}}+\mathrm{mG}\overset{\rightarrow} {\mathrm{B}}+\mathrm{2mG}\overset{\rightarrow} {\mathrm{C}}=\mathrm{0}\:\:'\mathrm{vector}' \\ $$$$\Rightarrow\left(\mathrm{4m}\right)\mathrm{G}\overset{\rightarrow} {\mathrm{A}}=−\mathrm{mA}\overset{\rightarrow} {\mathrm{B}}−\mathrm{2mA}\overset{\rightarrow} {\mathrm{C}} \\ $$$$\Rightarrow\mathrm{G}\overset{\rightarrow} {\mathrm{A}}=\frac{−\mathrm{A}\overset{\rightarrow} {\mathrm{B}}}{\mathrm{4}}−\mathrm{2}\frac{\mathrm{A}\overset{\rightarrow} {\mathrm{C}}}{\mathrm{4}} \\ $$$$\mathrm{A}\overset{\rightarrow} {\mathrm{B}}=\left(\mathrm{0}.\mathrm{t}−\mathrm{h}\right)=\left(\mathrm{0},\mathrm{l}\right) \\ $$$$\mathrm{A}\overset{\rightarrow} {\mathrm{C}}=\left(\mathrm{h},−\mathrm{h}\right) \\ $$$$\mathrm{G}\overset{\rightarrow} {\mathrm{A}}=\left(−\frac{\mathrm{h}}{\mathrm{2}},−\mathrm{l}+\frac{\mathrm{h}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\mathrm{A}\overset{\rightarrow} {\mathrm{G}}=\left(\frac{\mathrm{h}}{\mathrm{2}},\mathrm{l}−\frac{\mathrm{h}}{\mathrm{2}}\right) \\ $$$$\mathrm{G}\left(\mathrm{x},\mathrm{y}\right)\Rightarrow\begin{cases}{\mathrm{x}=\frac{\mathrm{h}}{\mathrm{2}}}\\{\mathrm{y}−\mathrm{h}=\mathrm{l}−\frac{\mathrm{h}}{\mathrm{2}}\Rightarrow\mathrm{y}=\mathrm{l}+\frac{\mathrm{h}}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{go}\:\mathrm{forther} \\ $$$$\mathrm{in}\:\mathrm{case}\:\mathrm{CB}=\mathrm{l} \\ $$$$\Rightarrow\left(\mathrm{h}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} \right)=\mathrm{l}^{\mathrm{2}} =\mid\mathrm{h}−\mathrm{t}\mid^{\mathrm{2}} =\mathrm{h}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} −\mathrm{2ht}\Rightarrow\mathrm{ht}=\mathrm{0} \\ $$$$\mathrm{CA}=\mathrm{l}\Rightarrow\mathrm{2h}^{\mathrm{2}} =\mathrm{l}^{\mathrm{2}} \Rightarrow\mathrm{h}=\underset{−} {+}\frac{\mathrm{l}}{\:\sqrt{\mathrm{2}}}\:\mathrm{we}\:\mathrm{have}\:\mathrm{4}\:\mathrm{case}\:\mathrm{if}\:\mathrm{we}\:\mathrm{want} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by TawaTawa last updated on 08/Nov/19
God bless you sir, Thanks for your time
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir},\:\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *