Menu Close

Question-7331

Tinku Tara 0 Comments
Pin




Question Number 7331 by rohit meena last updated on 23/Aug/16
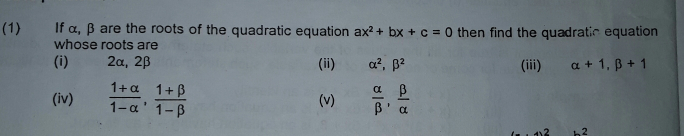
Commented by sandy_suhendra last updated on 24/Aug/16
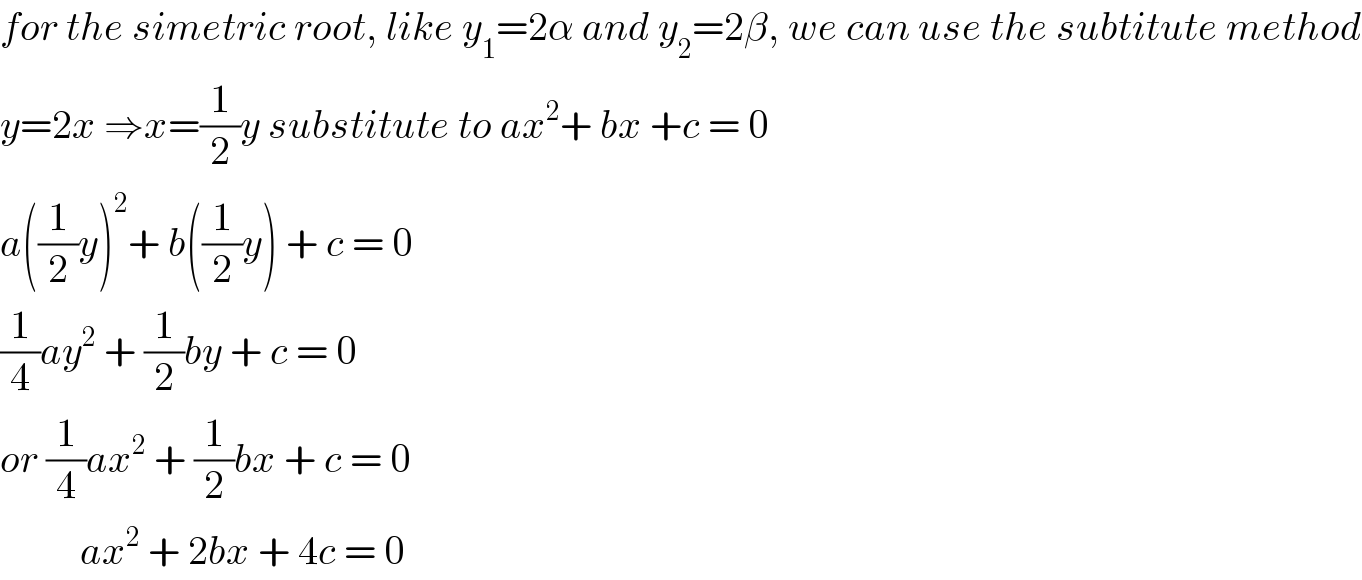
for the simetric root, like y_1 =2α and y_2 =2β, we can use the subtitute method y=2x ⇒x=(1/2)y substitute to ax^2 + bx +c = 0 a((1/2)y)^2 + b((1/2)y) + c = 0 (1/4)ay^2 + (1/2)by + c = 0 or (1/4)ax^2 + (1/2)bx + c = 0 ax^2 + 2bx + 4c = 0
$${for}\:{the}\:{simetric}\:{root},\:{like}\:{y}_{\mathrm{1}} =\mathrm{2}\alpha\:{and}\:{y}_{\mathrm{2}} =\mathrm{2}\beta,\:{we}\:{can}\:{use}\:{the}\:{subtitute}\:{method} \\ $$$${y}=\mathrm{2}{x}\:\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}{y}\:{substitute}\:{to}\:{ax}^{\mathrm{2}} +\:{bx}\:+{c}\:=\:\mathrm{0} \\ $$$${a}\left(\frac{\mathrm{1}}{\mathrm{2}}{y}\right)^{\mathrm{2}} +\:{b}\left(\frac{\mathrm{1}}{\mathrm{2}}{y}\right)\:+\:{c}\:=\:\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}{ay}^{\mathrm{2}} \:+\:\frac{\mathrm{1}}{\mathrm{2}}{by}\:+\:{c}\:=\:\mathrm{0} \\ $$$${or}\:\frac{\mathrm{1}}{\mathrm{4}}{ax}^{\mathrm{2}} \:+\:\frac{\mathrm{1}}{\mathrm{2}}{bx}\:+\:{c}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{ax}^{\mathrm{2}} \:+\:\mathrm{2}{bx}\:+\:\mathrm{4}{c}\:=\:\mathrm{0} \\ $$
Commented by Rasheed Soomro last updated on 24/Aug/16
New idea for me! There was a mistake in my answer.I have corrected now. By ′symetric roots′ you mean proportional roots? such as kα and kβ ?
$${New}\:{idea}\:{for}\:{me}!\:{There}\:{was}\:{a}\:{mistake} \\ $$$${in}\:{my}\:{answer}.{I}\:{have}\:{corrected}\:{now}. \\ $$$${By}\:'{symetric}\:{roots}'\:\:{you}\:{mean}\:{proportional} \\ $$$${roots}?\:{such}\:{as}\:{k}\alpha\:{and}\:{k}\beta\:? \\ $$
Commented by sandy_suhendra last updated on 25/Aug/16
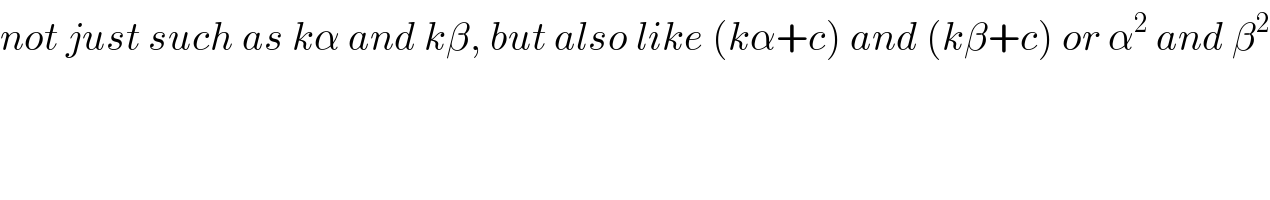
not just such as kα and kβ, but also like (kα+c) and (kβ+c) or α^2 and β^2
$${not}\:{just}\:{such}\:{as}\:{k}\alpha\:{and}\:{k}\beta,\:{but}\:{also}\:{like}\:\left({k}\alpha+{c}\right)\:{and}\:\left({k}\beta+{c}\right)\:{or}\:\alpha^{\mathrm{2}} \:{and}\:\beta^{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 25/Aug/16
THankS!
$$\mathcal{TH}{ank}\mathcal{S}! \\ $$
Answered by Rasheed Soomro last updated on 24/Aug/16
If α and β are the roots of ax^2 +bx+c=0, then α+β=−(b/a) and αβ=(c/a) Formula for determining equation, whose ′sum of the roots′ and ′product of the roots′ are given. x^2 −(sum of the roots)x+(product of the roots)=0 (i) 2α , 2β Required equation has sum of the roots =2α+2β=2(α+β)=2(−(b/a))=−((2b)/a) product of the roots=2α.2β=4αβ=4((c/a))=((4c)/a) Required equation will be x^2 −(−((2b)/a))x+(((4c)/a))=0 ax^2 +2bx+4c=0 (ii) α^2 ,β^2 Sum of the roots of required equation =α^2 +β^2 =(α+β)^2 −2αβ =(−(b/a))^2 −2((c/a))=((b^2 −ac)/a) Product of the roots of required equation =α^2 .β^2 =(αβ)^2 =((c/a))^2 =(c^2 /a^2 ) Required equation : x^2 −(((b^2 −ac)/a))x+((c^2 /a^2 ))=0 a^2 x^2 −a(b^2 −ac)x+c^2 =0 (iii) α+1,β+1 Sum of the roots of required equation =(α+1)+(β+1)=(α+β)+2 =(−(b/a))+2=((2−b)/a) Product of the roots of required equation =(α+1).(β+1)=αβ+α+β+1 =((c/a))+(−(b/a))+1=((a−b+c)/a) Required equation : x^2 −(((2−b)/a))x+(((a−b+c)/a))=0 ax^2 +(b−2)x+(a−b+c)=0 (iv) ((1+α)/(1−α)) , ((1+β)/(1−β)) Sum of the roots=((1+α)/(1−α)) + ((1+β)/(1−β))=(((1+α)(1−β)+(1+β)(1−α))/((1−α)(1−β))) =(((1−β+α−αβ)+(1−α+β−αβ))/(1−β−α+αβ)) =((1+(α−β)−αβ+1−(α−β)−αβ)/(1−(α+β)+αβ))=((2−2αβ)/(1−(α+β)+αβ))=((2−2((c/a)))/(1−(−(b/a))+(c/a))) =(((2a−2c)/a)/((a+b+c)/a))=((2(a−c))/(a+b+c)) Product of the roots=((1+α)/(1−α))× ((1+β)/(1−β))=((1+(α+β)+αβ)/(1−(α+β)+αβ))=((1+(−(b/a))+((c/a)))/(1−(−(b/a))+((c/a)))) =((a−b+c)/(a+b+c)) Required equation: x^2 −(((2(a−c))/(a+b+c)))x+((a−b+c)/(a+b+c))=0 (a+b+c)x^2 −2(a−c)x+(a−b+c)=0 (v) (α/β) ,(β/α) (v) Sum of the roots=(α/β)+(β/α)=((α^2 +β^2 )/(αβ))=(((α+β)^2 −2αβ)/(αβ)) =(((−(b/a))^2 −2((c/a)))/(c/a))=((b^2 −2ac)/a^2 )×(a/c)=((b^2 −2ac)/(ac)) Product of the roots=(α/β)×(β/α)=1 required equation x^2 −(((b^2 −2ac)/(ac)))x+1=0 acx^2 −(b^2 −2ac)x+ac=0
$${If}\:\alpha\:{and}\:\beta\:{are}\:{the}\:{roots}\:{of}\:\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0}, \\ $$$${then}\:\:\:\:\alpha+\beta=−\frac{{b}}{{a}}\:\:\:\:{and}\:\:\:\:\alpha\beta=\frac{{c}}{{a}} \\ $$$${Formula}\:{for}\:{determining}\:{equation},\:{whose} \\ $$$$'{sum}\:{of}\:{the}\:{roots}'\:\:{and}\:\:'{product}\:{of}\:{the}\:{roots}'\:{are}\:{given}. \\ $$$$\:\:\:\:\:\:\boldsymbol{{x}}^{\mathrm{2}} −\left(\boldsymbol{{sum}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{roots}}\right)\boldsymbol{{x}}+\left(\boldsymbol{{product}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{roots}}\right)=\mathrm{0} \\ $$$$ \\ $$$$\left({i}\right)\:\mathrm{2}\alpha\:,\:\mathrm{2}\beta \\ $$$${Required}\:{equation}\:{has} \\ $$$$\:\:\:{sum}\:{of}\:{the}\:{roots}\:=\mathrm{2}\alpha+\mathrm{2}\beta=\mathrm{2}\left(\alpha+\beta\right)=\mathrm{2}\left(−\frac{{b}}{{a}}\right)=−\frac{\mathrm{2}{b}}{{a}} \\ $$$$\:\:\:\:{product}\:{of}\:{the}\:{roots}=\mathrm{2}\alpha.\mathrm{2}\beta=\mathrm{4}\alpha\beta=\mathrm{4}\left(\frac{{c}}{{a}}\right)=\frac{\mathrm{4}{c}}{{a}} \\ $$$${Required}\:{equation}\:{will}\:{be} \\ $$$$\:\:\:\:{x}^{\mathrm{2}} −\left(−\frac{\mathrm{2}{b}}{{a}}\right){x}+\left(\frac{\mathrm{4}{c}}{{a}}\right)=\mathrm{0} \\ $$$$\:\:\:\:{ax}^{\mathrm{2}} +\mathrm{2}{bx}+\mathrm{4}{c}=\mathrm{0} \\ $$$$ \\ $$$$\left({ii}\right)\:\alpha^{\mathrm{2}} ,\beta^{\mathrm{2}} \\ $$$${Sum}\:{of}\:{the}\:{roots}\:{of}\:{required}\:{equation} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−\frac{{b}}{{a}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{c}}{{a}}\right)=\frac{{b}^{\mathrm{2}} −{ac}}{{a}} \\ $$$${Product}\:{of}\:{the}\:{roots}\:{of}\:{required}\:{equation} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\alpha^{\mathrm{2}} .\beta^{\mathrm{2}} =\left(\alpha\beta\right)^{\mathrm{2}} =\left(\frac{{c}}{{a}}\right)^{\mathrm{2}} =\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} } \\ $$$${Required}\:{equation}\:: \\ $$$$\:\:\:{x}^{\mathrm{2}} −\left(\frac{{b}^{\mathrm{2}} −{ac}}{{a}}\right){x}+\left(\frac{{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\:\:\:{a}^{\mathrm{2}} {x}^{\mathrm{2}} −{a}\left({b}^{\mathrm{2}} −{ac}\right){x}+{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$$\left({iii}\right)\:\alpha+\mathrm{1},\beta+\mathrm{1} \\ $$$${Sum}\:{of}\:{the}\:{roots}\:{of}\:{required}\:{equation} \\ $$$$\:\:\:\:\:\:=\left(\alpha+\mathrm{1}\right)+\left(\beta+\mathrm{1}\right)=\left(\alpha+\beta\right)+\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(−\frac{{b}}{{a}}\right)+\mathrm{2}=\frac{\mathrm{2}−{b}}{{a}} \\ $$$${Product}\:{of}\:{the}\:{roots}\:{of}\:{required}\:{equation} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left(\alpha+\mathrm{1}\right).\left(\beta+\mathrm{1}\right)=\alpha\beta+\alpha+\beta+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\frac{{c}}{{a}}\right)+\left(−\frac{{b}}{{a}}\right)+\mathrm{1}=\frac{{a}−{b}+{c}}{{a}} \\ $$$${Required}\:{equation}\:: \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\left(\frac{\mathrm{2}−{b}}{{a}}\right){x}+\left(\frac{{a}−{b}+{c}}{{a}}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:{ax}^{\mathrm{2}} +\left({b}−\mathrm{2}\right){x}+\left({a}−{b}+{c}\right)=\mathrm{0} \\ $$$$ \\ $$$$\left({iv}\right)\:\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}\:,\:\frac{\mathrm{1}+\beta}{\mathrm{1}−\beta} \\ $$$${Sum}\:{of}\:{the}\:{roots}=\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}\:+\:\frac{\mathrm{1}+\beta}{\mathrm{1}−\beta}=\frac{\left(\mathrm{1}+\alpha\right)\left(\mathrm{1}−\beta\right)+\left(\mathrm{1}+\beta\right)\left(\mathrm{1}−\alpha\right)}{\left(\mathrm{1}−\alpha\right)\left(\mathrm{1}−\beta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\mathrm{1}−\beta+\alpha−\alpha\beta\right)+\left(\mathrm{1}−\alpha+\beta−\alpha\beta\right)}{\mathrm{1}−\beta−\alpha+\alpha\beta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}+\left(\alpha−\beta\right)−\alpha\beta+\mathrm{1}−\left(\alpha−\beta\right)−\alpha\beta}{\mathrm{1}−\left(\alpha+\beta\right)+\alpha\beta}=\frac{\mathrm{2}−\mathrm{2}\alpha\beta}{\mathrm{1}−\left(\alpha+\beta\right)+\alpha\beta}=\frac{\mathrm{2}−\mathrm{2}\left(\frac{{c}}{{a}}\right)}{\mathrm{1}−\left(−\frac{{b}}{{a}}\right)+\frac{{c}}{{a}}} \\ $$$$=\frac{\frac{\mathrm{2}{a}−\mathrm{2}{c}}{{a}}}{\frac{{a}+{b}+{c}}{{a}}}=\frac{\mathrm{2}\left({a}−{c}\right)}{{a}+{b}+{c}} \\ $$$${Product}\:{of}\:{the}\:{roots}=\frac{\mathrm{1}+\alpha}{\mathrm{1}−\alpha}×\:\frac{\mathrm{1}+\beta}{\mathrm{1}−\beta}=\frac{\mathrm{1}+\left(\alpha+\beta\right)+\alpha\beta}{\mathrm{1}−\left(\alpha+\beta\right)+\alpha\beta}=\frac{\mathrm{1}+\left(−\frac{{b}}{{a}}\right)+\left(\frac{{c}}{{a}}\right)}{\mathrm{1}−\left(−\frac{{b}}{{a}}\right)+\left(\frac{{c}}{{a}}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{a}−{b}+{c}}{{a}+{b}+{c}} \\ $$$${Required}\:{equation}:\:{x}^{\mathrm{2}} −\left(\frac{\mathrm{2}\left({a}−{c}\right)}{{a}+{b}+{c}}\right){x}+\frac{{a}−{b}+{c}}{{a}+{b}+{c}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}+{b}+{c}\right){x}^{\mathrm{2}} −\mathrm{2}\left({a}−{c}\right){x}+\left({a}−{b}+{c}\right)=\mathrm{0} \\ $$$$\left({v}\right)\:\frac{\alpha}{\beta}\:,\frac{\beta}{\alpha} \\ $$$$\left({v}\right)\:\:{Sum}\:{of}\:{the}\:{roots}=\frac{\alpha}{\beta}+\frac{\beta}{\alpha}=\frac{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} }{\alpha\beta}=\frac{\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta}{\alpha\beta} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\left(−\frac{{b}}{{a}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{c}}{{a}}\right)}{\frac{{c}}{{a}}}=\frac{{b}^{\mathrm{2}} −\mathrm{2}{ac}}{{a}^{\mathrm{2}} }×\frac{{a}}{{c}}=\frac{{b}^{\mathrm{2}} −\mathrm{2}{ac}}{{ac}} \\ $$$${Product}\:{of}\:{the}\:{roots}=\frac{\alpha}{\beta}×\frac{\beta}{\alpha}=\mathrm{1} \\ $$$${required}\:{equation}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\left(\frac{{b}^{\mathrm{2}} −\mathrm{2}{ac}}{{ac}}\right){x}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{acx}^{\mathrm{2}} −\left({b}^{\mathrm{2}} −\mathrm{2}{ac}\right){x}+{ac}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *