Question Number 73525 by arkanmath7@gmail.com last updated on 13/Nov/19

Commented by mathmax by abdo last updated on 13/Nov/19
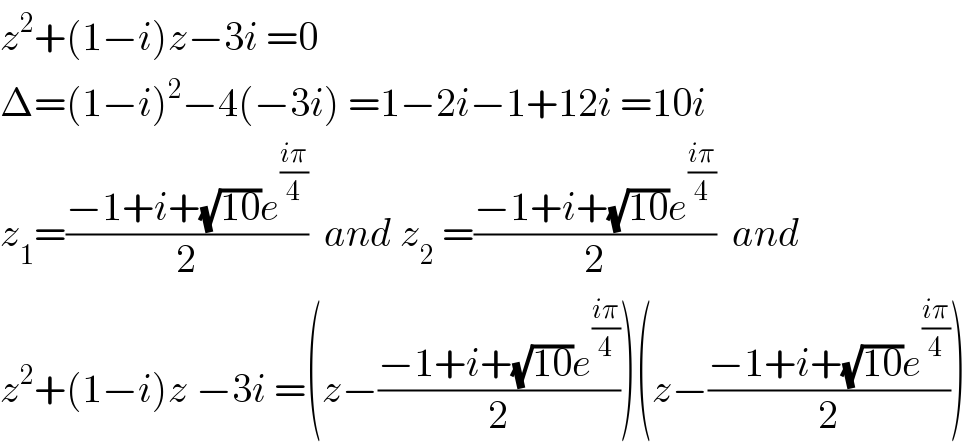
$${z}^{\mathrm{2}} +\left(\mathrm{1}−{i}\right){z}−\mathrm{3}{i}\:=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{1}−{i}\right)^{\mathrm{2}} −\mathrm{4}\left(−\mathrm{3}{i}\right)\:=\mathrm{1}−\mathrm{2}{i}−\mathrm{1}+\mathrm{12}{i}\:=\mathrm{10}{i} \\ $$$${z}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}+\sqrt{\mathrm{10}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}}\:\:{and}\:{z}_{\mathrm{2}} \:=\frac{−\mathrm{1}+{i}+\sqrt{\mathrm{10}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}}\:\:{and} \\ $$$${z}^{\mathrm{2}} +\left(\mathrm{1}−{i}\right){z}\:−\mathrm{3}{i}\:=\left({z}−\frac{−\mathrm{1}+{i}+\sqrt{\mathrm{10}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}}\right)\left({z}−\frac{−\mathrm{1}+{i}+\sqrt{\mathrm{10}}{e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}}\right) \\ $$
Commented by arkanmath7@gmail.com last updated on 15/Nov/19

$${thnx} \\ $$
Answered by MJS last updated on 13/Nov/19
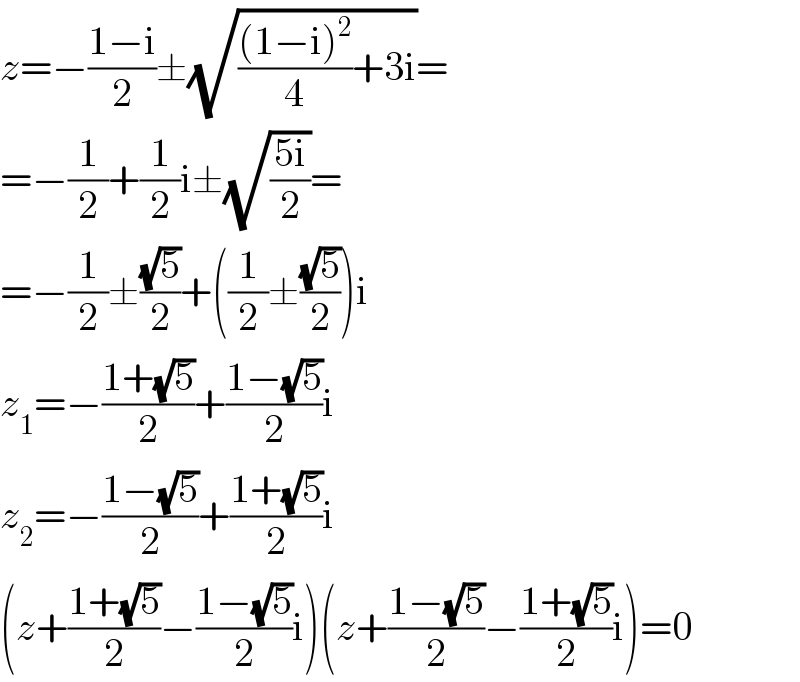
$${z}=−\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}}\pm\sqrt{\frac{\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{2}} }{\mathrm{4}}+\mathrm{3i}}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{i}\pm\sqrt{\frac{\mathrm{5i}}{\mathrm{2}}}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\left(\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\mathrm{i} \\ $$$${z}_{\mathrm{1}} =−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{i} \\ $$$${z}_{\mathrm{2}} =−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{i} \\ $$$$\left({z}+\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{i}\right)\left({z}+\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\mathrm{i}\right)=\mathrm{0} \\ $$
