Menu Close

Question-73730

Tinku Tara 0 Comments
Pin




Question Number 73730 by TawaTawa last updated on 15/Nov/19
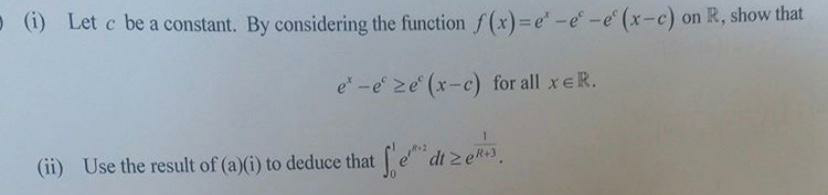
Answered by mind is power last updated on 15/Nov/19
f(x)=e^x −e^c −e^c (x−c) ⇒f′(x)=e^x −e^c ⇒ { ((f(′x)≥0,∀x≥c)),((f′(x)≤0,∀x≤c)) :} ⇒min f=f(c)=0⇒∀x∈R,f(x)≥0⇔e^x −e^c ≥e^c (x−c) ∫_0 ^1 e^t^(R+1) dt we have for c=0⇒e^x −1≥1(x−1)⇔e^x ≥x,x=t^(R+2) ⇒e^t^(R+2) ≥t^(R+2) ⇒∫_0 ^1 e^t^(R+2) ≥∫_0 ^1 t^(R+2) =(1/(R+3))
$${f}\left({x}\right)={e}^{{x}} −{e}^{{c}} −{e}^{{c}} \left({x}−{c}\right) \\ $$$$\Rightarrow{f}'\left({x}\right)={e}^{{x}} −{e}^{{c}} \Rightarrow\begin{cases}{{f}\left('{x}\right)\geqslant\mathrm{0},\forall{x}\geqslant{c}}\\{{f}'\left({x}\right)\leqslant\mathrm{0},\forall{x}\leqslant{c}}\end{cases} \\ $$$$\Rightarrow{min}\:{f}={f}\left({c}\right)=\mathrm{0}\Rightarrow\forall{x}\in\mathbb{R},{f}\left({x}\right)\geqslant\mathrm{0}\Leftrightarrow{e}^{{x}} −{e}^{{c}} \geqslant{e}^{{c}} \left({x}−{c}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}^{{R}+\mathrm{1}} } {dt} \\ $$$${we}\:{have}\:{for}\:{c}=\mathrm{0}\Rightarrow{e}^{{x}} −\mathrm{1}\geqslant\mathrm{1}\left({x}−\mathrm{1}\right)\Leftrightarrow{e}^{{x}} \geqslant{x},{x}={t}^{{R}+\mathrm{2}} \\ $$$$\Rightarrow{e}^{{t}^{{R}+\mathrm{2}} } \geqslant{t}^{{R}+\mathrm{2}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}^{{R}+\mathrm{2}} } \geqslant\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{R}+\mathrm{2}} =\frac{\mathrm{1}}{{R}+\mathrm{3}} \\ $$
Commented by TawaTawa last updated on 15/Nov/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mind is power last updated on 15/Nov/19
y′re welcom sir
$${y}'{re}\:{welcom}\:{sir} \\ $$
Answered by mind is power last updated on 15/Nov/19
∫_0 ^1 e^t^(R+2) dt≥e^(1/(R+3)) sorry my previous answer when i zoomed e did not appear we use a(i) for x=t^(R+2) ,and c=(1/(R+3)) ⇒e^t^(R+2) −e^(1/(R+3)) ≥e^(1/(R+3)) (t^(R+2) −(1/(R+3))) ⇒∫_0 ^1 (e^t^(R+2) −e^(1/(R+3)) )dt≥∫e^(1/(R+3)) (t^(R+2) −(1/(R+3)))dt=e^(1/(R+3)) ∫_0 ^1 (t^(R+2) −(1/(R+3)))dt=0 ⇒∫_0 ^1 (e^t^(R+2) −e^(1/(R+3)) )dt≥0 ∫_0 ^1 (e^t^(R+2) −e^(1/(R+3)) )dt=∫_0 ^1 e^t^(R+2) dt−e^(1/(R+3)) ≥0⇒∫_0 ^1 e^t^(R+2) ≥e^(1/(R+3))
$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}^{{R}+\mathrm{2}} } {dt}\geqslant{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \:\:{sorry}\:{my}\:{previous}\:{answer}\:{when}\:{i}\:{zoomed}\:{e}\:{did}\:{not}\:{appear} \\ $$$${we}\:{use}\:{a}\left({i}\right)\:{for}\:{x}={t}^{{R}+\mathrm{2}} ,{and}\:{c}=\frac{\mathrm{1}}{{R}+\mathrm{3}} \\ $$$$\Rightarrow{e}^{{t}^{{R}+\mathrm{2}} } −{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \geqslant{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \left({t}^{{R}+\mathrm{2}} −\frac{\mathrm{1}}{{R}+\mathrm{3}}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \left({e}^{{t}^{{R}+\mathrm{2}} } −{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \right){dt}\geqslant\int{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \left({t}^{{R}+\mathrm{2}} −\frac{\mathrm{1}}{{R}+\mathrm{3}}\right){dt}={e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \int_{\mathrm{0}} ^{\mathrm{1}} \left({t}^{{R}+\mathrm{2}} −\frac{\mathrm{1}}{{R}+\mathrm{3}}\right){dt}=\mathrm{0} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \left({e}^{{t}^{{R}+\mathrm{2}} } −{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \right){dt}\geqslant\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left({e}^{{t}^{{R}+\mathrm{2}} } −{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \right){dt}=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}^{{R}+\mathrm{2}} } {dt}−{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \geqslant\mathrm{0}\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}^{{R}+\mathrm{2}} } \geqslant{e}^{\frac{\mathrm{1}}{{R}+\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$
Commented by TawaTawa last updated on 15/Nov/19
Thanks for your time sir. God bless you.
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by mind is power last updated on 15/Nov/19
y′re welcom
$${y}'{re}\:{welcom} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *