Question Number 73737 by ajfour last updated on 15/Nov/19

Commented by ajfour last updated on 15/Nov/19

$${Find}\:{R}/{r}\:. \\ $$
Answered by ajfour last updated on 15/Nov/19
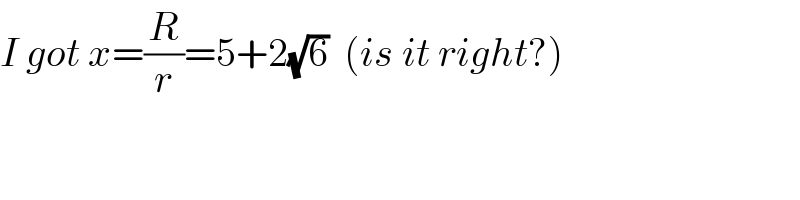
$${I}\:{got}\:{x}=\frac{{R}}{{r}}=\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\:\:\left({is}\:{it}\:{right}?\right) \\ $$
Commented by mr W last updated on 15/Nov/19

$${correct}\:{sir}! \\ $$
Answered by mr W last updated on 15/Nov/19
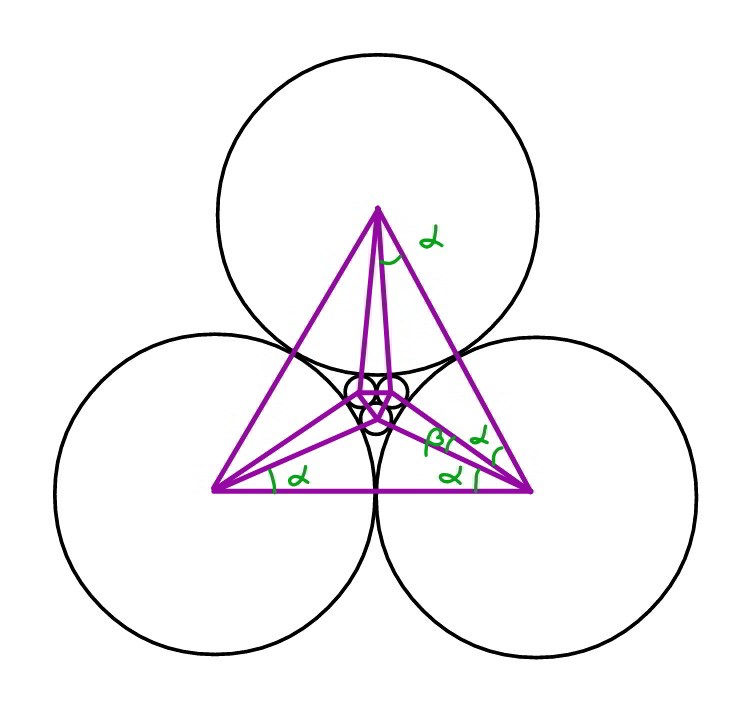
Commented by mr W last updated on 15/Nov/19
![[(2/3)(√3)r+(√((R+r)^2 −R^2 ))]×2=(1/3)(√3)r+(√((R+r)^2 −r^2 )) (√3)r+2(√(r(2R+r)))=(√(R(R+2Rr))) 4r(√(3r(2R+r)))=(R−7r)(R+r) R^4 −12R^3 r+22R^2 r^2 −12Rr^3 +r^2 =0 (R−r)^2 (R^2 −10Rr+r^2 )=0 ⇒R=(5+2(√6))r](https://www.tinkutara.com/question/Q73776.png)
$$\left[\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\mathrm{3}}{r}+\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }\right]×\mathrm{2}=\frac{\mathrm{1}}{\mathrm{3}}\sqrt{\mathrm{3}}{r}+\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\sqrt{\mathrm{3}}{r}+\mathrm{2}\sqrt{{r}\left(\mathrm{2}{R}+{r}\right)}=\sqrt{{R}\left({R}+\mathrm{2}{Rr}\right)} \\ $$$$\mathrm{4}{r}\sqrt{\mathrm{3}{r}\left(\mathrm{2}{R}+{r}\right)}=\left({R}−\mathrm{7}{r}\right)\left({R}+{r}\right) \\ $$$${R}^{\mathrm{4}} −\mathrm{12}{R}^{\mathrm{3}} {r}+\mathrm{22}{R}^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{12}{Rr}^{\mathrm{3}} +{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} \left({R}^{\mathrm{2}} −\mathrm{10}{Rr}+{r}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{R}=\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right){r} \\ $$
Commented by ajfour last updated on 15/Nov/19
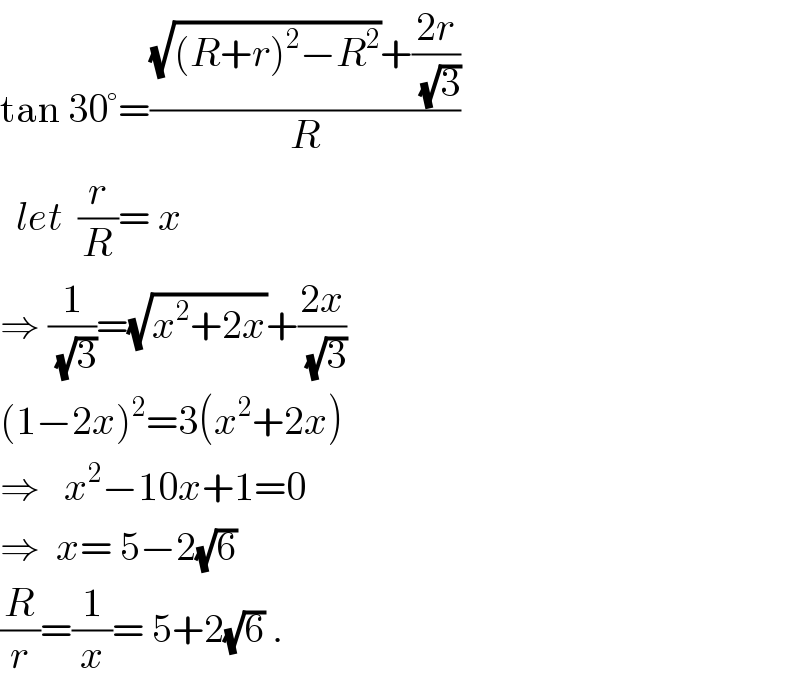
$$\mathrm{tan}\:\mathrm{30}°=\frac{\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }+\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{3}}}}{{R}} \\ $$$$\:\:{let}\:\:\frac{{r}}{{R}}=\:{x} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}}+\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{3}}} \\ $$$$\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{2}} =\mathrm{3}\left({x}^{\mathrm{2}} +\mathrm{2}{x}\right) \\ $$$$\Rightarrow\:\:\:{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}=\:\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{1}}{{x}}=\:\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\:. \\ $$
Commented by ajfour last updated on 15/Nov/19
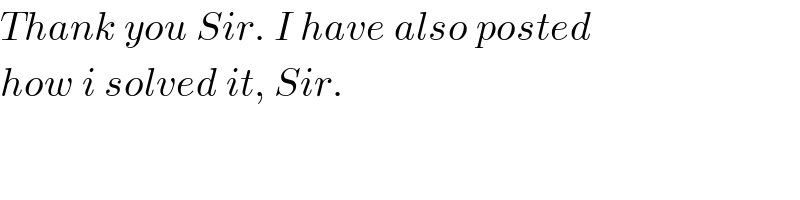
$${Thank}\:{you}\:{Sir}.\:{I}\:{have}\:{also}\:{posted} \\ $$$${how}\:{i}\:{solved}\:{it},\:{Sir}. \\ $$
Commented by mr W last updated on 15/Nov/19

$${very}\:{nice}! \\ $$$${your}\:{path}\:{is}\:{better},\:{since}\:{it}\:{yields} \\ $$$${a}\:{quadratic}\:{equation}. \\ $$
