Question Number 73832 by FCB last updated on 16/Nov/19

Commented by FCB last updated on 16/Nov/19

$$\boldsymbol{\mathrm{solve}} \\ $$
Commented by MJS last updated on 16/Nov/19
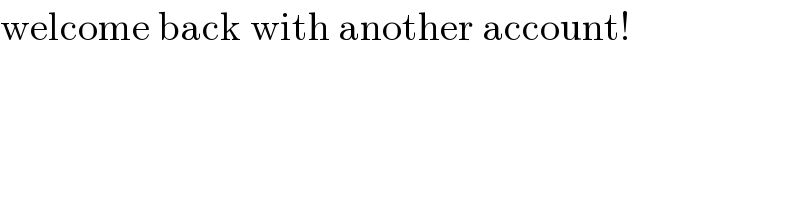
$$\mathrm{welcome}\:\mathrm{back}\:\mathrm{with}\:\mathrm{another}\:\mathrm{account}! \\ $$
Commented by peter frank last updated on 16/Nov/19
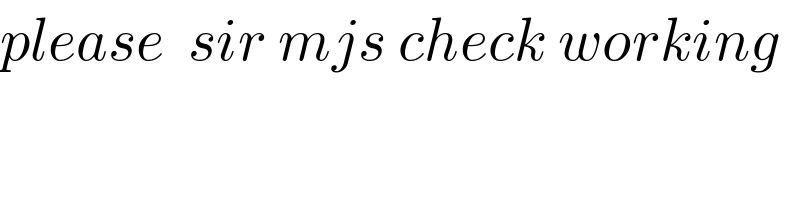
$${please}\:\:{sir}\:{mjs}\:{check}\:{working} \\ $$$$ \\ $$
Commented by MJS last updated on 16/Nov/19
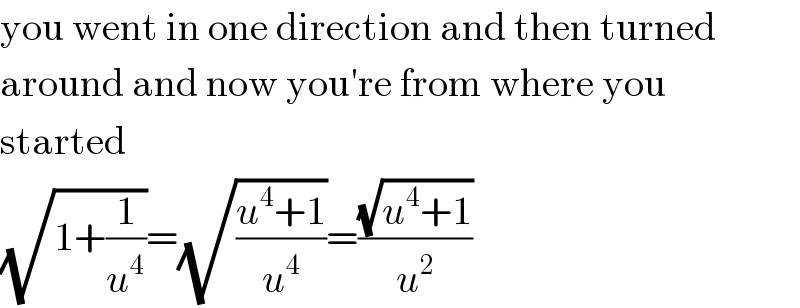
$$\mathrm{you}\:\mathrm{went}\:\mathrm{in}\:\mathrm{one}\:\mathrm{direction}\:\mathrm{and}\:\mathrm{then}\:\mathrm{turned} \\ $$$$\mathrm{around}\:\mathrm{and}\:\mathrm{now}\:\mathrm{you}'\mathrm{re}\:\mathrm{from}\:\mathrm{where}\:\mathrm{you} \\ $$$$\mathrm{started} \\ $$$$\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{4}} }}=\sqrt{\frac{{u}^{\mathrm{4}} +\mathrm{1}}{{u}^{\mathrm{4}} }}=\frac{\sqrt{{u}^{\mathrm{4}} +\mathrm{1}}}{{u}^{\mathrm{2}} } \\ $$
Commented by peter frank last updated on 16/Nov/19
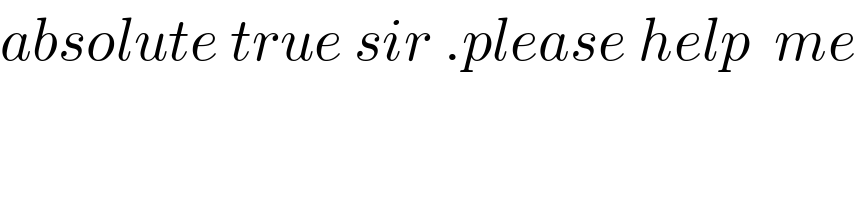
$${absolute}\:{true}\:{sir}\:.{please}\:{help}\:\:{me} \\ $$
Commented by FCB last updated on 16/Nov/19

$$???? \\ $$
Commented by MJS last updated on 16/Nov/19
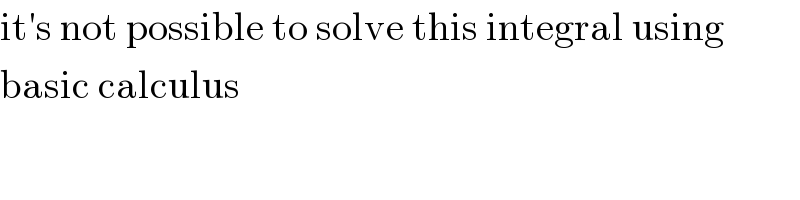
$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{using} \\ $$$$\mathrm{basic}\:\mathrm{calculus} \\ $$
Answered by peter frank last updated on 16/Nov/19
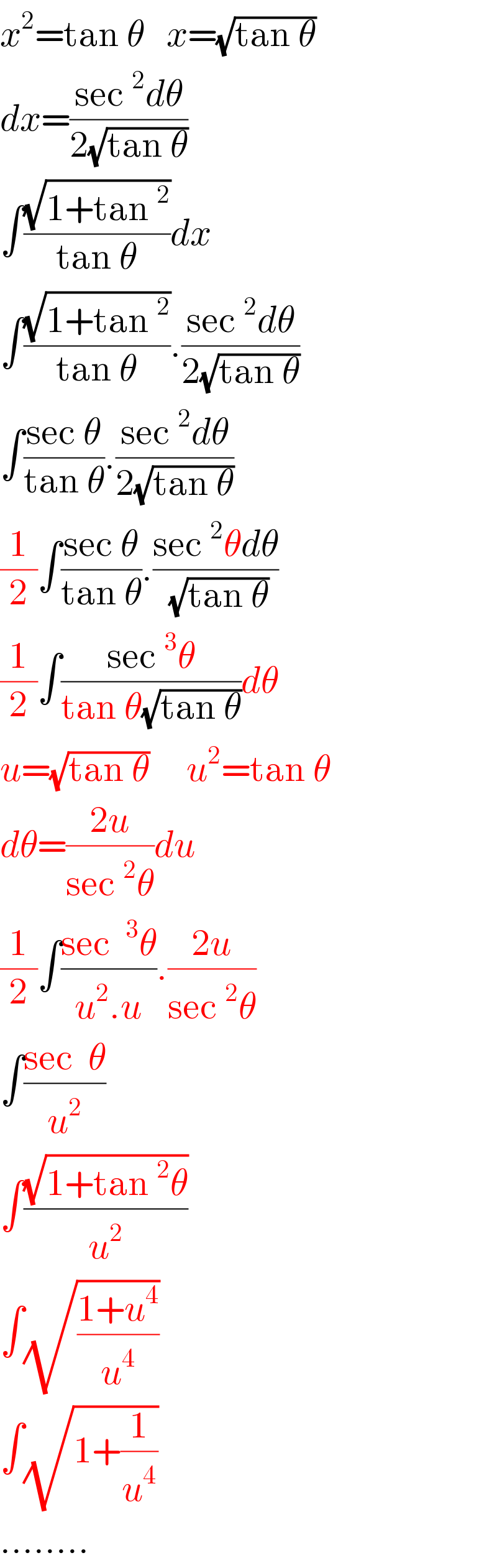
$${x}^{\mathrm{2}} =\mathrm{tan}\:\theta\:\:\:{x}=\sqrt{\mathrm{tan}\:\theta} \\ $$$${dx}=\frac{\mathrm{sec}\:^{\mathrm{2}} {d}\theta}{\mathrm{2}\sqrt{\mathrm{tan}\:\theta}} \\ $$$$\int\frac{\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} }}{\mathrm{tan}\:\theta}{dx} \\ $$$$\int\frac{\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} }}{\mathrm{tan}\:\theta}.\frac{\mathrm{sec}\:^{\mathrm{2}} {d}\theta}{\mathrm{2}\sqrt{\mathrm{tan}\:\theta}} \\ $$$$\int\frac{\mathrm{sec}\:\theta}{\mathrm{tan}\:\theta}.\frac{\mathrm{sec}\:^{\mathrm{2}} {d}\theta}{\mathrm{2}\sqrt{\mathrm{tan}\:\theta}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{sec}\:\theta}{\mathrm{tan}\:\theta}.\frac{\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{\:\sqrt{\mathrm{tan}\:\theta}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{sec}\:^{\mathrm{3}} \theta}{\mathrm{tan}\:\theta\sqrt{\mathrm{tan}\:\theta}}{d}\theta \\ $$$${u}=\sqrt{\mathrm{tan}\:\theta}\:\:\:\:\:{u}^{\mathrm{2}} =\mathrm{tan}\:\theta \\ $$$${d}\theta=\frac{\mathrm{2}{u}}{\mathrm{sec}\:^{\mathrm{2}} \theta}{du} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{sec}\:\:^{\mathrm{3}} \theta}{{u}^{\mathrm{2}} .{u}}.\frac{\mathrm{2}{u}}{\mathrm{sec}\:^{\mathrm{2}} \theta} \\ $$$$\int\frac{\mathrm{sec}\:\:\theta}{{u}^{\mathrm{2}} } \\ $$$$\int\frac{\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}}{{u}^{\mathrm{2}} } \\ $$$$\int\sqrt{\frac{\mathrm{1}+{u}^{\mathrm{4}} }{{u}^{\mathrm{4}} }} \\ $$$$\int\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{4}} }} \\ $$$$…….. \\ $$
Commented by FCB last updated on 16/Nov/19

Commented by FCB last updated on 16/Nov/19

$$\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{that}} \\ $$
Commented by FCB last updated on 16/Nov/19

Commented by FCB last updated on 16/Nov/19

$$\mathrm{sir}\:\mathrm{peter}\:\mathrm{frank}\:? \\ $$
Commented by peter frank last updated on 16/Nov/19
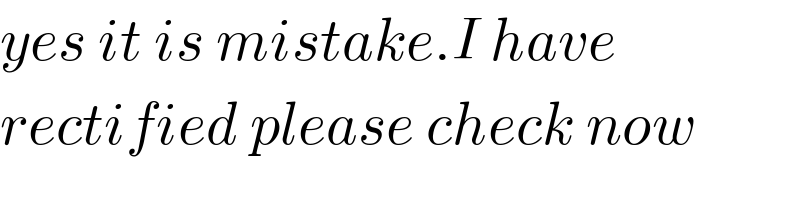
$${yes}\:{it}\:{is}\:{mistake}.{I}\:{have} \\ $$$${rectified}\:{please}\:{check}\:{now} \\ $$
Commented by mind is power last updated on 16/Nov/19
![∫((√(1+x^4 ))/x^2 )dx=((−(√(1+x^4 )))/x)+∫((2x^3 )/(x(√(1+x^4 ))))dx we devloppe ∫((2x^2 )/( (√(1+x^4 ))))dx x=e^(i(π/4)) .sh(t)⇒dx=e^(i(π/4)) ch(t) ⇒∫_0 ^x ((2x^2 dx)/( (√(1+x^4 ))))=2e^(i(π/4)) ∫_0 ^(sh^− (xe^(−((iπ)/4)) )) .((ish^2 (t)ch(t))/( (√(1−sh^4 (t))))) =2ie^(i(π/4)) ∫_0 ^(sh^− (xe^(−((iπ)/4)) )) ((sh^2 (t)ch(t))/( (√((1−sh^2 (t))(1+sh^2 (t))))))dt =2ie^(i(π/4)) ∫_0 ^(sh^− (xe^(−((iπ)/4)) )) ((sh^2 (t)ch(t))/( (√(1−sh^2 (t))).ch(t)))dt 2ie^(i(π/4)) ∫_0 ^(sh^− (xe^(−((iπ)/4)) )) ((sh^2 (t))/( (√(1−sh^2 (t))).))dt t=is sh(is)=isin(s) ⇔−2e^(i(π/4)) ∫_0 ^(−ish^− (xe^(−((iπ)/4)) )) ((sin^2 (t))/( (√(1+sin^2 (t))))) ⇔−2e^(i(π/4)) ∫_0 ^(−ish^− (xe^(−((iπ)/4)) )) ((sin^2 (t)+1−1)/( (√(1+sin^2 (t))))) ⇔−2e^(i(π/4)) ∫_0 ^(−ish^− (xe^(−((iπ)/4)) )) (√(1−(i)^2 sin^2 (t)))−2(−e^(i(π/4)) )∫_0 ^(−ish^− (xe^(−((iπ)/4)) )) (dt/( (√(1−(i)^2 sin^2 (t))))) E(θ⌋k^2 )=∫_0 ^θ (dϕ/( (√(1−k^2 sin^2 (ϕ))))),2nd eleptic function F(θ]k^2 )=∫_0 ^θ (√(1−(k^2 )sin^2 (ϕ)))dϕ so we get −2e^(i(π/4)) F(−ish^− (xe^(i(π/4)) )∣−1)−(−2e^(i(π/4)) )E(−ish(xe^(i(π/4)) )∣−1) to finish e^(i(π/4)) =(−1)^(1/4) ∫((√(1+x^4 ))/x^2 )dx=((−(√(1+x^4 )))/x)+∫((2x^3 )/(x(√(1+x^4 ))))dx −((√(1+x^4 ))/x)=−(1/(x(√(1+x^4 ))))−(x^3 /( (√(1+x^4 )))) we get the answer](https://www.tinkutara.com/question/Q73947.png)
$$\int\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\frac{−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}}+\int\frac{\mathrm{2x}^{\mathrm{3}} }{\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\mathrm{dx} \\ $$$$\mathrm{we}\:\:\mathrm{devloppe} \\ $$$$\int\frac{\mathrm{2x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\mathrm{dx} \\ $$$$\mathrm{x}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} .\mathrm{sh}\left(\mathrm{t}\right)\Rightarrow\mathrm{dx}=\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \mathrm{ch}\left(\mathrm{t}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{x}} \frac{\mathrm{2x}^{\mathrm{2}} \mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}=\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{\mathrm{sh}^{−} \left(\mathrm{xe}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} .\frac{\mathrm{ish}^{\mathrm{2}} \left(\mathrm{t}\right)\mathrm{ch}\left(\mathrm{t}\right)}{\:\sqrt{\mathrm{1}−\mathrm{sh}^{\mathrm{4}} \left(\mathrm{t}\right)}} \\ $$$$=\mathrm{2ie}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{\mathrm{sh}^{−} \left(\mathrm{xe}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \frac{\mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)\mathrm{ch}\left(\mathrm{t}\right)}{\:\sqrt{\left(\mathrm{1}−\mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)\right)\left(\mathrm{1}+\mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)\right)}}\mathrm{dt} \\ $$$$=\mathrm{2ie}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{\mathrm{sh}^{−} \left(\mathrm{xe}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \frac{\mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)\mathrm{ch}\left(\mathrm{t}\right)}{\:\sqrt{\mathrm{1}−\mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)}.\mathrm{ch}\left(\mathrm{t}\right)}\mathrm{dt} \\ $$$$\mathrm{2ie}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{\mathrm{sh}^{−} \left(\mathrm{xe}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \frac{\mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)}{\:\sqrt{\mathrm{1}−\mathrm{sh}^{\mathrm{2}} \left(\mathrm{t}\right)}.}\mathrm{dt} \\ $$$$\mathrm{t}=\mathrm{is} \\ $$$$\mathrm{sh}\left(\mathrm{is}\right)=\mathrm{isin}\left(\mathrm{s}\right) \\ $$$$\Leftrightarrow−\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{−\mathrm{ish}^{−} \left(\mathrm{xe}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}\right)}{\:\sqrt{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}\right)}} \\ $$$$\Leftrightarrow−\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{−\mathrm{ish}^{−} \left(\mathrm{xe}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}\right)+\mathrm{1}−\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}\right)}} \\ $$$$\Leftrightarrow−\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \int_{\mathrm{0}} ^{−\mathrm{ish}^{−} \left(\mathrm{xe}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \sqrt{\mathrm{1}−\left(\mathrm{i}\right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}\right)}−\mathrm{2}\left(−\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)\int_{\mathrm{0}} ^{−\mathrm{ish}^{−} \left(\mathrm{xe}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \right)} \frac{\mathrm{dt}}{\:\sqrt{\mathrm{1}−\left(\mathrm{i}\right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{t}\right)}} \\ $$$$\mathrm{E}\left(\theta\rfloor\mathrm{k}^{\mathrm{2}} \right)=\int_{\mathrm{0}} ^{\theta} \frac{\mathrm{d}\varphi}{\:\sqrt{\mathrm{1}−\mathrm{k}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \left(\varphi\right)}},\mathrm{2nd}\:\mathrm{eleptic}\:\:\mathrm{function} \\ $$$$\left.\mathrm{F}\left(\theta\right]\mathrm{k}^{\mathrm{2}} \right)=\int_{\mathrm{0}} ^{\theta} \sqrt{\mathrm{1}−\left(\mathrm{k}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \left(\varphi\right)}\mathrm{d}\varphi \\ $$$$\mathrm{so}\:\mathrm{we}\:\mathrm{get} \\ $$$$−\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \mathrm{F}\left(−\mathrm{ish}^{−} \left(\mathrm{xe}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)\mid−\mathrm{1}\right)−\left(−\mathrm{2e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)\mathrm{E}\left(−\mathrm{ish}\left(\mathrm{xe}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \right)\mid−\mathrm{1}\right) \\ $$$$\mathrm{to}\:\mathrm{finish}\:\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} =\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\int\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\frac{−\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}}+\int\frac{\mathrm{2x}^{\mathrm{3}} }{\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}\mathrm{dx} \\ $$$$−\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}}=−\frac{\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}−\frac{\mathrm{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{answer} \\ $$$$ \\ $$$$ \\ $$
Commented by MJS last updated on 17/Nov/19

$$\mathrm{yes};\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by mind is power last updated on 17/Nov/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom}\:\mathrm{sir} \\ $$
Commented by FCB last updated on 17/Nov/19

$$\mathrm{great}! \\ $$
Answered by Tanmay chaudhury last updated on 17/Nov/19

