Question Number 73940 by smartsmith459@gmail.com last updated on 16/Nov/19

Answered by Rio Michael last updated on 16/Nov/19
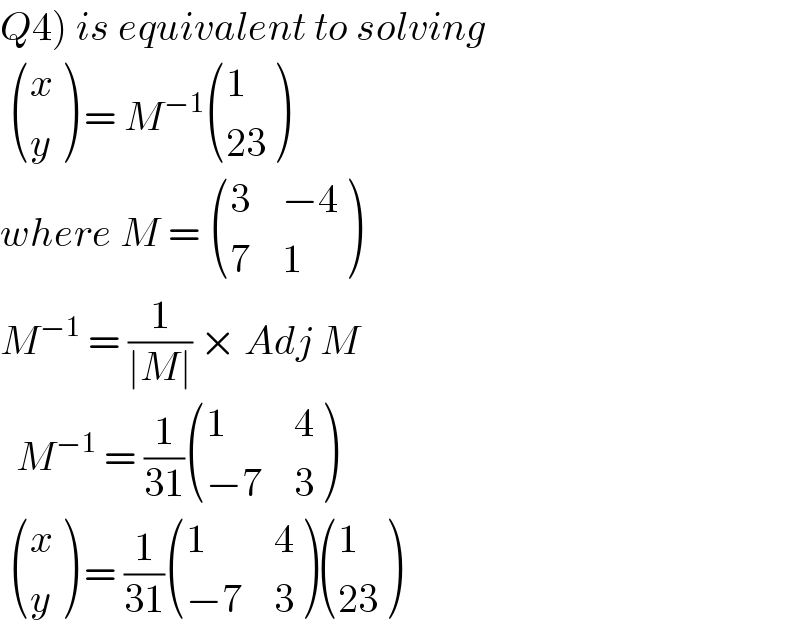
$$\left.{Q}\mathrm{4}\right)\:{is}\:{equivalent}\:{to}\:{solving}\: \\ $$$$\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:{M}^{−\mathrm{1}} \begin{pmatrix}{\mathrm{1}}\\{\mathrm{23}}\end{pmatrix} \\ $$$${where}\:{M}\:=\:\begin{pmatrix}{\mathrm{3}}&{−\mathrm{4}}\\{\mathrm{7}}&{\mathrm{1}}\end{pmatrix} \\ $$$${M}^{−\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mid{M}\mid}\:×\:{Adj}\:{M} \\ $$$$\:\:{M}^{−\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{31}}\begin{pmatrix}{\mathrm{1}}&{\mathrm{4}}\\{−\mathrm{7}}&{\mathrm{3}}\end{pmatrix} \\ $$$$\:\begin{pmatrix}{{x}}\\{{y}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{\mathrm{31}}\begin{pmatrix}{\mathrm{1}}&{\mathrm{4}}\\{−\mathrm{7}}&{\mathrm{3}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}}\\{\mathrm{23}}\end{pmatrix} \\ $$
