Question-7397

Question Number 7397 by Tawakalitu. last updated on 26/Aug/16

Answered by sandy_suhendra last updated on 27/Aug/16

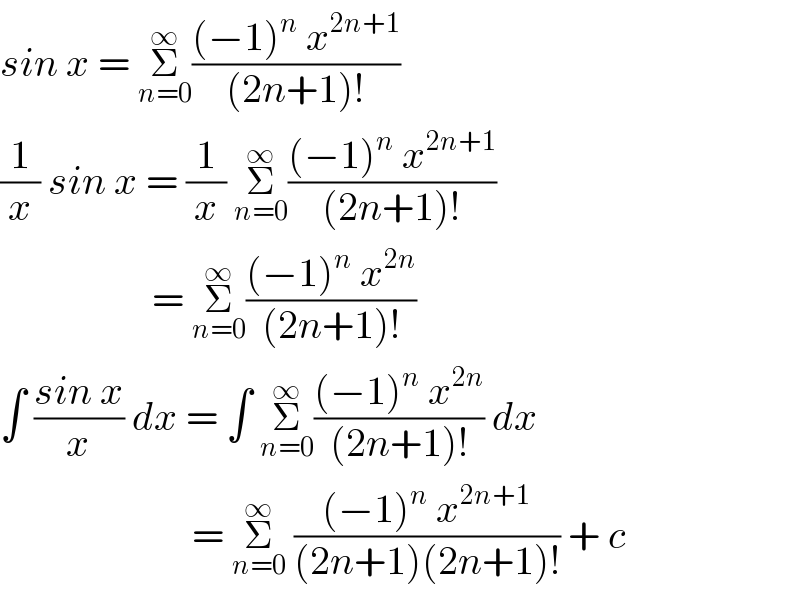
sin x = Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) (1/x) sin x = (1/x) Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)!)) = Σ_(n=0) ^∞ (((−1)^n x^(2n) )/((2n+1)!)) ∫ ((sin x)/x) dx = ∫ Σ_(n=0) ^∞ (((−1)^n x^(2n) )/((2n+1)!)) dx = Σ_(n=0) ^∞ (((−1)^n x^(2n+1) )/((2n+1)(2n+1)!)) + c

$${sin}\:{x}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\frac{\mathrm{1}}{{x}}\:{sin}\:{x}\:=\:\frac{\mathrm{1}}{{x}}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\int\:\frac{{sin}\:{x}}{{x}}\:{dx}\:=\:\int\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:+\:{c} \\ $$

Commented by Tawakalitu. last updated on 27/Aug/16

$${Thank}\:{you}\:{for}\:{your}\:{time}.\:{i}\:{really}\:{appreciate} \\ $$

Facebook Tweet Pin

Question-7397

Leave a Reply Cancel reply