Question Number 7407 by Tawakalitu. last updated on 27/Aug/16

Commented by sou1618 last updated on 27/Aug/16
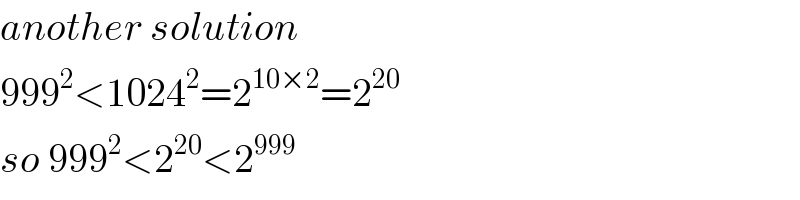
$${another}\:{solution} \\ $$$$\mathrm{999}^{\mathrm{2}} <\mathrm{1024}^{\mathrm{2}} =\mathrm{2}^{\mathrm{10}×\mathrm{2}} =\mathrm{2}^{\mathrm{20}} \\ $$$${so}\:\mathrm{999}^{\mathrm{2}} <\mathrm{2}^{\mathrm{20}} <\mathrm{2}^{\mathrm{999}} \\ $$
Commented by Tawakalitu. last updated on 27/Aug/16

$${Thanks}\:{so}\:{much} \\ $$
Answered by sandy_suhendra last updated on 28/Aug/16
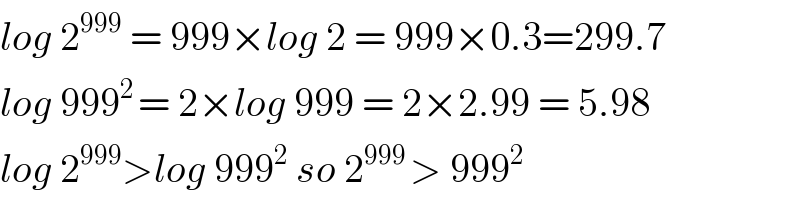
$${log}\:\mathrm{2}^{\mathrm{999}} \:=\:\mathrm{999}×{log}\:\mathrm{2}\:=\:\mathrm{999}×\mathrm{0}.\mathrm{3}=\mathrm{299}.\mathrm{7} \\ $$$${log}\:\mathrm{999}^{\mathrm{2}\:} =\:\mathrm{2}×{log}\:\mathrm{999}\:=\:\mathrm{2}×\mathrm{2}.\mathrm{99}\:=\:\mathrm{5}.\mathrm{98} \\ $$$${log}\:\mathrm{2}^{\mathrm{999}} >{log}\:\mathrm{999}^{\mathrm{2}} \:{so}\:\mathrm{2}^{\mathrm{999}\:} >\:\mathrm{999}^{\mathrm{2}} \\ $$
Commented by Tawakalitu. last updated on 27/Aug/16

$${Thanks}\:{so}\:{much}. \\ $$
Answered by FilupSmith last updated on 28/Aug/16
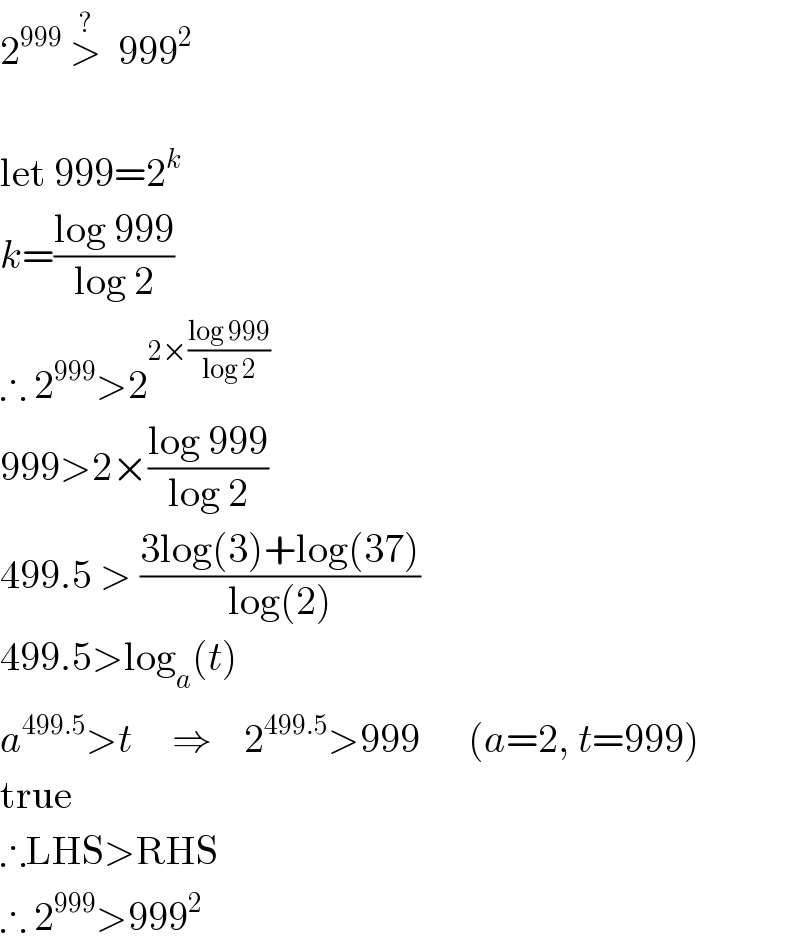
$$\mathrm{2}^{\mathrm{999}} \:\overset{?} {>}\:\:\mathrm{999}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{let}\:\mathrm{999}=\mathrm{2}^{{k}} \\ $$$${k}=\frac{\mathrm{log}\:\mathrm{999}}{\mathrm{log}\:\mathrm{2}} \\ $$$$\therefore\:\mathrm{2}^{\mathrm{999}} >\mathrm{2}^{\mathrm{2}×\frac{\mathrm{log}\:\mathrm{999}}{\mathrm{log}\:\mathrm{2}}} \\ $$$$\mathrm{999}>\mathrm{2}×\frac{\mathrm{log}\:\mathrm{999}}{\mathrm{log}\:\mathrm{2}} \\ $$$$\mathrm{499}.\mathrm{5}\:>\:\frac{\mathrm{3log}\left(\mathrm{3}\right)+\mathrm{log}\left(\mathrm{37}\right)}{\mathrm{log}\left(\mathrm{2}\right)} \\ $$$$\mathrm{499}.\mathrm{5}>\mathrm{log}_{{a}} \left({t}\right) \\ $$$${a}^{\mathrm{499}.\mathrm{5}} >{t}\:\:\:\:\:\Rightarrow\:\:\:\:\mathrm{2}^{\mathrm{499}.\mathrm{5}} >\mathrm{999}\:\:\:\:\:\:\left({a}=\mathrm{2},\:{t}=\mathrm{999}\right) \\ $$$$\mathrm{true} \\ $$$$\therefore\mathrm{LHS}>\mathrm{RHS} \\ $$$$\therefore\:\mathrm{2}^{\mathrm{999}} >\mathrm{999}^{\mathrm{2}} \\ $$
Commented by FilupSmith last updated on 28/Aug/16
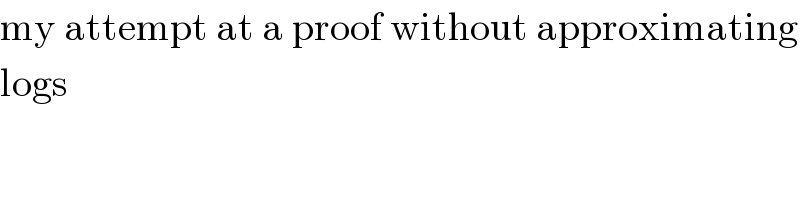
$$\mathrm{my}\:\mathrm{attempt}\:\mathrm{at}\:\mathrm{a}\:\mathrm{proof}\:\mathrm{without}\:\mathrm{approximating} \\ $$$$\mathrm{logs} \\ $$
