Question Number 74209 by FCB last updated on 20/Nov/19
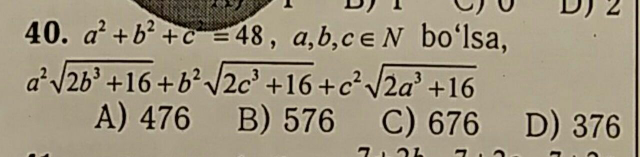
Answered by mind is power last updated on 20/Nov/19
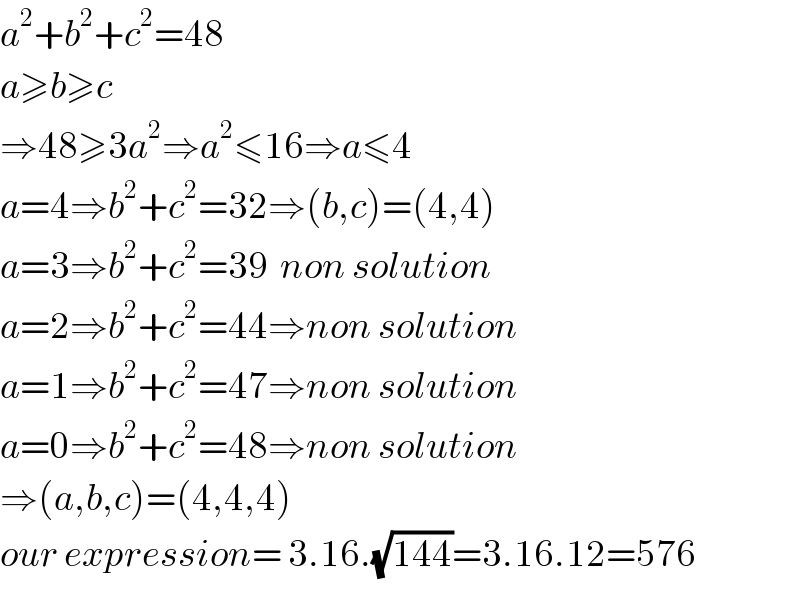
$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{48} \\ $$$${a}\geqslant{b}\geqslant{c} \\ $$$$\Rightarrow\mathrm{48}\geqslant\mathrm{3}{a}^{\mathrm{2}} \Rightarrow{a}^{\mathrm{2}} \leqslant\mathrm{16}\Rightarrow{a}\leqslant\mathrm{4} \\ $$$${a}=\mathrm{4}\Rightarrow{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{32}\Rightarrow\left({b},{c}\right)=\left(\mathrm{4},\mathrm{4}\right) \\ $$$${a}=\mathrm{3}\Rightarrow{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{39}\:\:{non}\:{solution} \\ $$$${a}=\mathrm{2}\Rightarrow{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{44}\Rightarrow{non}\:{solution} \\ $$$${a}=\mathrm{1}\Rightarrow{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{47}\Rightarrow{non}\:{solution} \\ $$$${a}=\mathrm{0}\Rightarrow{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{48}\Rightarrow{non}\:{solution} \\ $$$$\Rightarrow\left({a},{b},{c}\right)=\left(\mathrm{4},\mathrm{4},\mathrm{4}\right) \\ $$$${our}\:{expression}=\:\mathrm{3}.\mathrm{16}.\sqrt{\mathrm{144}}=\mathrm{3}.\mathrm{16}.\mathrm{12}=\mathrm{576} \\ $$
