Menu Close

Question-74213

Tinku Tara 0 Comments
Pin




Question Number 74213 by FCB last updated on 20/Nov/19
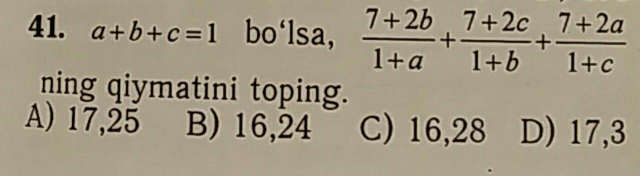
Commented by MJS last updated on 20/Nov/19
information missing I think the question is find minimum of the expression this should be at a=b=c=(1/3) in this case the answer is ((69)/4)=17.25
$$\mathrm{information}\:\mathrm{missing} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{find}\:\mathrm{minimum}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{expression} \\ $$$$\mathrm{this}\:\mathrm{should}\:\mathrm{be}\:\mathrm{at}\:{a}={b}={c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{69}}{\mathrm{4}}=\mathrm{17}.\mathrm{25} \\ $$
Answered by mind is power last updated on 20/Nov/19
what is quation ?
$${what}\:{is}\:{quation}\:? \\ $$
Answered by mind is power last updated on 20/Nov/19
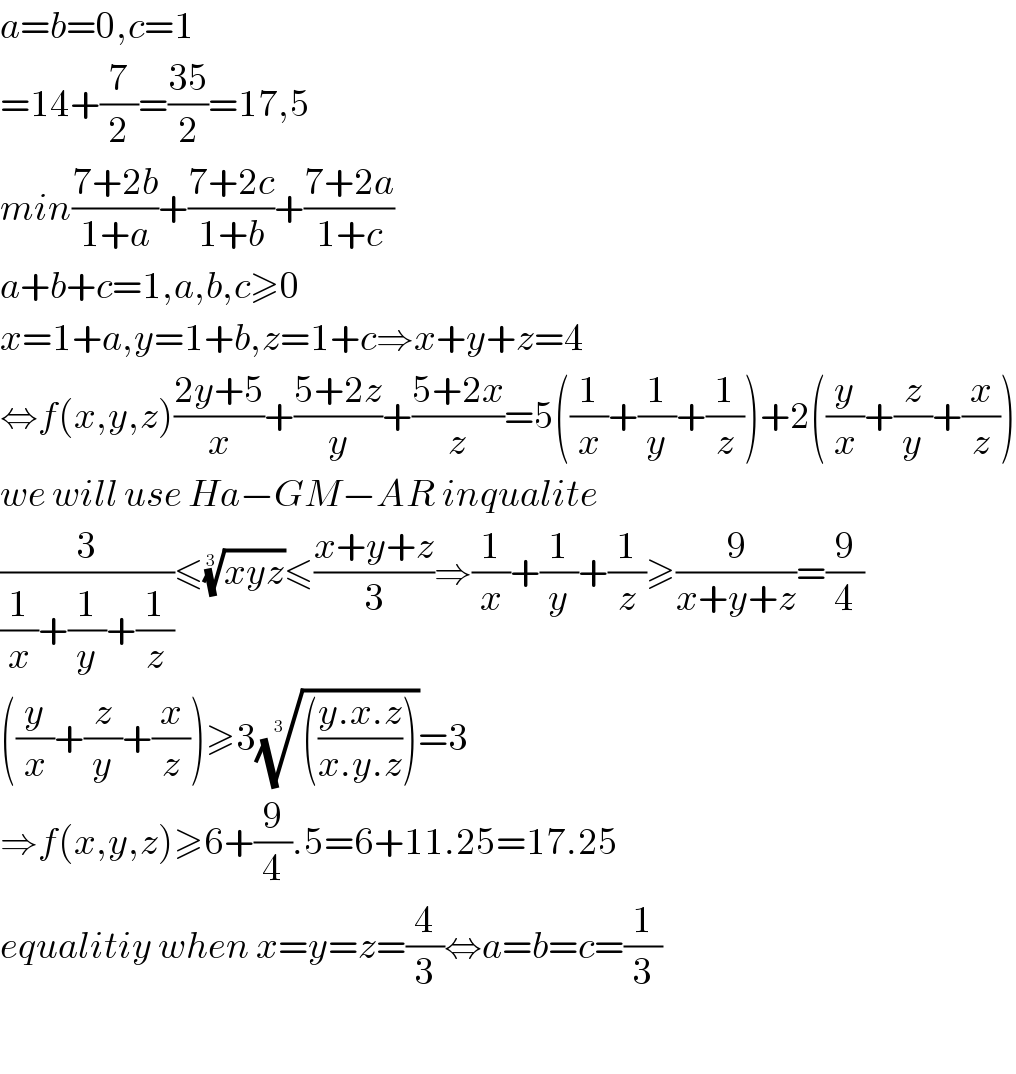
a=b=0,c=1 =14+(7/2)=((35)/2)=17,5 min((7+2b)/(1+a))+((7+2c)/(1+b))+((7+2a)/(1+c)) a+b+c=1,a,b,c≥0 x=1+a,y=1+b,z=1+c⇒x+y+z=4 ⇔f(x,y,z)((2y+5)/x)+((5+2z)/y)+((5+2x)/z)=5((1/x)+(1/y)+(1/z))+2((y/x)+(z/y)+(x/z)) we will use Ha−GM−AR inqualite (3/((1/x)+(1/y)+(1/z)))≤((xyz))^(1/3) ≤((x+y+z)/3)⇒(1/x)+(1/y)+(1/z)≥(9/(x+y+z))=(9/4) ((y/x)+(z/y)+(x/z))≥3(((((y.x.z)/(x.y.z)))))^(1/3) =3 ⇒f(x,y,z)≥6+(9/4).5=6+11.25=17.25 equalitiy when x=y=z=(4/3)⇔a=b=c=(1/3)
$${a}={b}=\mathrm{0},{c}=\mathrm{1} \\ $$$$=\mathrm{14}+\frac{\mathrm{7}}{\mathrm{2}}=\frac{\mathrm{35}}{\mathrm{2}}=\mathrm{17},\mathrm{5}\: \\ $$$${min}\frac{\mathrm{7}+\mathrm{2}{b}}{\mathrm{1}+{a}}+\frac{\mathrm{7}+\mathrm{2}{c}}{\mathrm{1}+{b}}+\frac{\mathrm{7}+\mathrm{2}{a}}{\mathrm{1}+{c}} \\ $$$${a}+{b}+{c}=\mathrm{1},{a},{b},{c}\geqslant\mathrm{0} \\ $$$${x}=\mathrm{1}+{a},{y}=\mathrm{1}+{b},{z}=\mathrm{1}+{c}\Rightarrow{x}+{y}+{z}=\mathrm{4} \\ $$$$\Leftrightarrow{f}\left({x},{y},{z}\right)\frac{\mathrm{2}{y}+\mathrm{5}}{{x}}+\frac{\mathrm{5}+\mathrm{2}{z}}{{y}}+\frac{\mathrm{5}+\mathrm{2}{x}}{{z}}=\mathrm{5}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right)+\mathrm{2}\left(\frac{{y}}{{x}}+\frac{{z}}{{y}}+\frac{{x}}{{z}}\right) \\ $$$${we}\:{will}\:{use}\:{Ha}−{GM}−{AR}\:{inqualite} \\ $$$$\frac{\mathrm{3}}{\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}}\leqslant\sqrt[{\mathrm{3}}]{{xyz}}\leqslant\frac{{x}+{y}+{z}}{\mathrm{3}}\Rightarrow\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\geqslant\frac{\mathrm{9}}{{x}+{y}+{z}}=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\left(\frac{{y}}{{x}}+\frac{{z}}{{y}}+\frac{{x}}{{z}}\right)\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\left(\frac{{y}.{x}.{z}}{{x}.{y}.{z}}\right)}=\mathrm{3} \\ $$$$\Rightarrow{f}\left({x},{y},{z}\right)\geqslant\mathrm{6}+\frac{\mathrm{9}}{\mathrm{4}}.\mathrm{5}=\mathrm{6}+\mathrm{11}.\mathrm{25}=\mathrm{17}.\mathrm{25}\: \\ $$$${equalitiy}\:{when}\:{x}={y}={z}=\frac{\mathrm{4}}{\mathrm{3}}\Leftrightarrow{a}={b}={c}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *