Question Number 74231 by necxxx last updated on 20/Nov/19
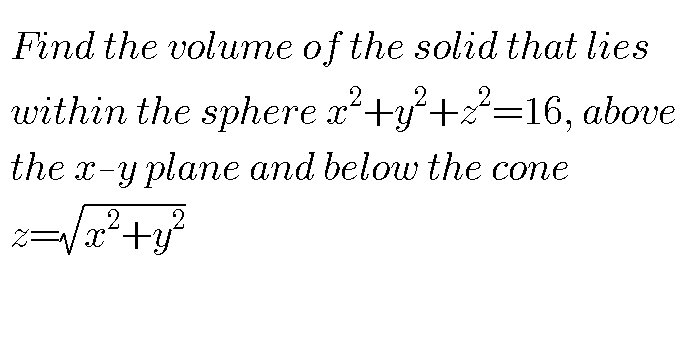
Commented by necxxx last updated on 20/Nov/19

Commented by necxxx last updated on 20/Nov/19

$${here}\:{was}\:{a}\:{step}\:{taken}\:{though}\:{not}\:{so} \\ $$$${sure}.\:{Please}\:{I}\:{need}\:{help}.\:{Thanks}\:{in} \\ $$$${advance}. \\ $$
Answered by mind is power last updated on 20/Nov/19
![Z=(√(x^2 +y^2 ))∩(x^2 +y^2 +z^2 =16)⇒2(x^2 +y^2 )=16 ⇒x^2 +y^2 =8 intersection over circle center 0≤r≤4 , −(π/2)≤θ≤(π/2), −π≤α≤π x=rcos(θ)cos(α) y=rcos(θ)sin(α) z=rsin(θ) 0≤Z≤(√(x^2 +y^2 )) ⇒ 0≤rsin(θ)≤(√(r^2 cos^2 (θ)))=rcos(θ) ⇒0≤sin(θ)≤cos(θ)⇒θ∈[0,(π/4)] V=∫_0 ^4 ∫_0 ^(π/4) ∫_(−π) ^π r^2 sin(θ)dαdθdr =∫_0 ^4 r^2 dr.∫_0 ^(π/4) sin(θ)dθ.∫_(−π) ^π dα =((64)/3).(1−((√2)/2)).2π =(2−(√2)).((64π)/3)](https://www.tinkutara.com/question/Q74243.png)
$${Z}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\cap\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{16}\right)\Rightarrow\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)=\mathrm{16} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{8} \\ $$$${intersection}\:{over}\:{circle}\:{center}\:\: \\ $$$$\mathrm{0}\leqslant{r}\leqslant\mathrm{4}\:\:\:,\:\:−\frac{\pi}{\mathrm{2}}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}},\:\:\:−\pi\leqslant\alpha\leqslant\pi \\ $$$${x}={rcos}\left(\theta\right){cos}\left(\alpha\right) \\ $$$${y}={rcos}\left(\theta\right){sin}\left(\alpha\right) \\ $$$${z}={rsin}\left(\theta\right) \\ $$$$\:\:\:\:\:\mathrm{0}\leqslant{Z}\leqslant\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{0}\leqslant{rsin}\left(\theta\right)\leqslant\sqrt{{r}^{\mathrm{2}} {cos}^{\mathrm{2}} \left(\theta\right)}={rcos}\left(\theta\right) \\ $$$$\Rightarrow\mathrm{0}\leqslant{sin}\left(\theta\right)\leqslant{cos}\left(\theta\right)\Rightarrow\theta\in\left[\mathrm{0},\frac{\pi}{\mathrm{4}}\right] \\ $$$${V}=\int_{\mathrm{0}} ^{\mathrm{4}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \int_{−\pi} ^{\pi} {r}^{\mathrm{2}} {sin}\left(\theta\right){d}\alpha{d}\theta{dr} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} {r}^{\mathrm{2}} {dr}.\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {sin}\left(\theta\right){d}\theta.\int_{−\pi} ^{\pi} {d}\alpha \\ $$$$=\frac{\mathrm{64}}{\mathrm{3}}.\left(\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right).\mathrm{2}\pi \\ $$$$=\left(\mathrm{2}−\sqrt{\mathrm{2}}\right).\frac{\mathrm{64}\pi}{\mathrm{3}} \\ $$
Commented by necxxx last updated on 25/Nov/19
$${oh}…{Thank}\:{you}\:{so}\:{much}. \\ $$
