Question-74323

Question Number 74323 by arthur.kangdani@gmail.com last updated on 22/Nov/19

Commented by arthur.kangdani@gmail.com last updated on 22/Nov/19

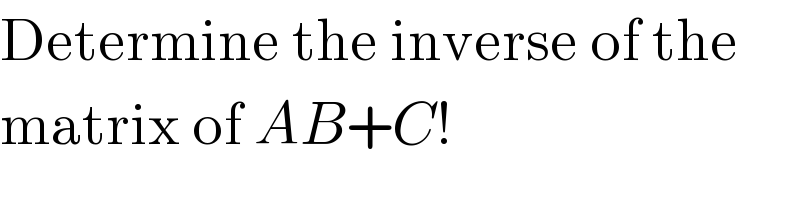
Determine the inverse of the matrix of AB+C!

$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{inverse}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{matrix}\:\mathrm{of}\:{AB}+{C}! \\ $$

Commented by mathmax by abdo last updated on 22/Nov/19

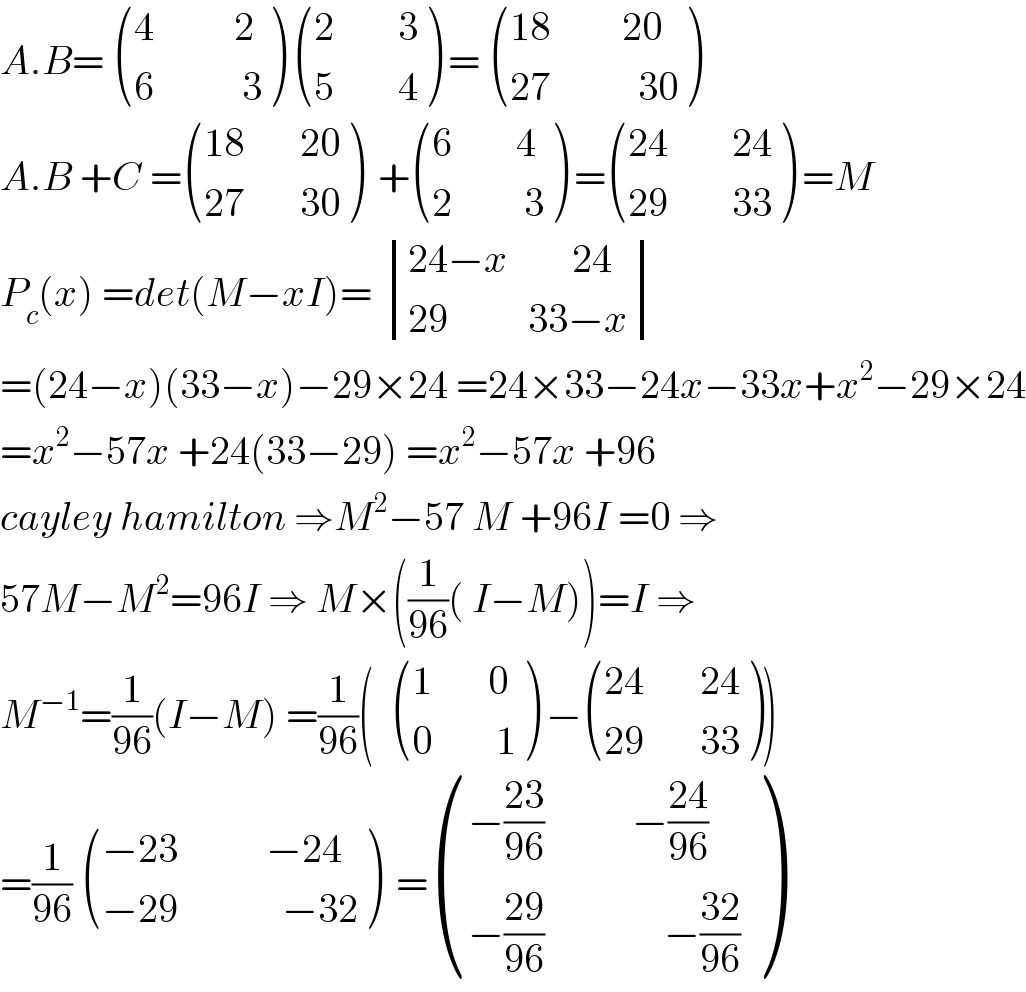
A.B= (((4 2)),((6 3)) ) (((2 3)),((5 4)) ) = (((18 20)),((27 30)) ) A.B +C = (((18 20)),((27 30)) ) + (((6 4)),((2 3)) ) = (((24 24)),((29 33)) ) =M P_c (x) =det(M−xI)= determinant (((24−x 24)),((29 33−x))) =(24−x)(33−x)−29×24 =24×33−24x−33x+x^2 −29×24 =x^2 −57x +24(33−29) =x^2 −57x +96 cayley hamilton ⇒M^2 −57 M +96I =0 ⇒ 57M−M^2 =96I ⇒ M×((1/(96))( I−M))=I ⇒ M^(−1) =(1/(96))(I−M) =(1/(96))( (((1 0)),((0 1)) ) − (((24 24)),((29 33)) )) =(1/(96)) (((−23 −24)),((−29 −32)) ) = (((−((23)/(96)) −((24)/(96)))),((−((29)/(96)) −((32)/(96)))) )

$${A}.{B}=\:\begin{pmatrix}{\mathrm{4}\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\\{\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{3}}\\{\mathrm{5}\:\:\:\:\:\:\:\:\mathrm{4}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{18}\:\:\:\:\:\:\:\:\:\mathrm{20}}\\{\mathrm{27}\:\:\:\:\:\:\:\:\:\:\:\mathrm{30}}\end{pmatrix} \\ $$$${A}.{B}\:+{C}\:=\begin{pmatrix}{\mathrm{18}\:\:\:\:\:\:\:\mathrm{20}}\\{\mathrm{27}\:\:\:\:\:\:\:\mathrm{30}}\end{pmatrix}\:\:+\begin{pmatrix}{\mathrm{6}\:\:\:\:\:\:\:\:\mathrm{4}}\\{\mathrm{2}\:\:\:\:\:\:\:\:\:\mathrm{3}}\end{pmatrix}\:=\begin{pmatrix}{\mathrm{24}\:\:\:\:\:\:\:\:\mathrm{24}}\\{\mathrm{29}\:\:\:\:\:\:\:\:\mathrm{33}}\end{pmatrix}\:={M} \\ $$$${P}_{{c}} \left({x}\right)\:={det}\left({M}−{xI}\right)=\:\begin{vmatrix}{\mathrm{24}−{x}\:\:\:\:\:\:\:\:\mathrm{24}}\\{\mathrm{29}\:\:\:\:\:\:\:\:\:\:\mathrm{33}−{x}}\end{vmatrix} \\ $$$$=\left(\mathrm{24}−{x}\right)\left(\mathrm{33}−{x}\right)−\mathrm{29}×\mathrm{24}\:=\mathrm{24}×\mathrm{33}−\mathrm{24}{x}−\mathrm{33}{x}+{x}^{\mathrm{2}} −\mathrm{29}×\mathrm{24} \\ $$$$={x}^{\mathrm{2}} −\mathrm{57}{x}\:+\mathrm{24}\left(\mathrm{33}−\mathrm{29}\right)\:={x}^{\mathrm{2}} −\mathrm{57}{x}\:+\mathrm{96} \\ $$$${cayley}\:{hamilton}\:\Rightarrow{M}^{\mathrm{2}} −\mathrm{57}\:{M}\:+\mathrm{96}{I}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{57}{M}−{M}^{\mathrm{2}} =\mathrm{96}{I}\:\Rightarrow\:{M}×\left(\frac{\mathrm{1}}{\mathrm{96}}\left(\:{I}−{M}\right)\right)={I}\:\Rightarrow \\ $$$${M}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{96}}\left({I}−{M}\right)\:=\frac{\mathrm{1}}{\mathrm{96}}\left(\:\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:−\begin{pmatrix}{\mathrm{24}\:\:\:\:\:\:\:\mathrm{24}}\\{\mathrm{29}\:\:\:\:\:\:\:\mathrm{33}}\end{pmatrix}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{96}}\:\begin{pmatrix}{−\mathrm{23}\:\:\:\:\:\:\:\:\:\:\:−\mathrm{24}}\\{−\mathrm{29}\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{32}}\end{pmatrix}\:\:=\begin{pmatrix}{−\frac{\mathrm{23}}{\mathrm{96}}\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{24}}{\mathrm{96}}}\\{−\frac{\mathrm{29}}{\mathrm{96}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{32}}{\mathrm{96}}}\end{pmatrix} \\ $$

Commented by abdomathmax last updated on 22/Nov/19

error at lime 7 M×(57I−M)=96 I ⇒ M×[(1/(96))( 57 I−M)]=I ⇒ M^(−1) =(1/(96)){ (((57 0)),((0 57)) ) − (((24 24)),((29 33)) )} =(1/(96)) (((33 −24)),((−29 24)) )=....

$${error}\:{at}\:{lime}\:\mathrm{7}\:\:{M}×\left(\mathrm{57}{I}−{M}\right)=\mathrm{96}\:{I}\:\Rightarrow \\ $$$${M}×\left[\frac{\mathrm{1}}{\mathrm{96}}\left(\:\mathrm{57}\:{I}−{M}\right)\right]={I}\:\Rightarrow \\ $$$${M}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{96}}\left\{\:\begin{pmatrix}{\mathrm{57}\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{57}}\end{pmatrix}\:−\begin{pmatrix}{\mathrm{24}\:\:\:\:\:\:\:\:\mathrm{24}}\\{\mathrm{29}\:\:\:\:\:\:\:\:\:\mathrm{33}}\end{pmatrix}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{96}}\:\begin{pmatrix}{\mathrm{33}\:\:\:\:\:\:\:\:\:−\mathrm{24}}\\{−\mathrm{29}\:\:\:\:\:\:\:\:\:\mathrm{24}}\end{pmatrix}=…. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply