Question-74328

Question Number 74328 by arthur.kangdani@gmail.com last updated on 22/Nov/19

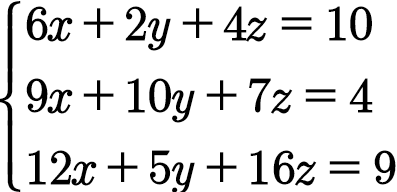
Answered by ajfour last updated on 22/Nov/19

x = \frac{{| \begin{matrix} 10 & 2 & 4 \\ 4 & 10 & 7 \\ 9 & 5 & 16 \end{matrix} |}_{}}{{| \begin{matrix} 6 & 2 & 4 \\ 9 & 10 & 7 \\ 12 & 5 & 16 \end{matrix} |}^{}}

\Rightarrow x = \frac{10 (160 - 35) - 2 (64 - 63) + 4 (20 - 90)}{6 (160 - 35) - 2 (144 - 84) + 4 (45 - 120)}

x = \frac{1250 - 2 - 280}{750 - 120 - 300} = \frac{968}{330} = \frac{88}{30}

\dots . .

Facebook Tweet Pin