Question-74383

Question Number 74383 by aliesam last updated on 23/Nov/19

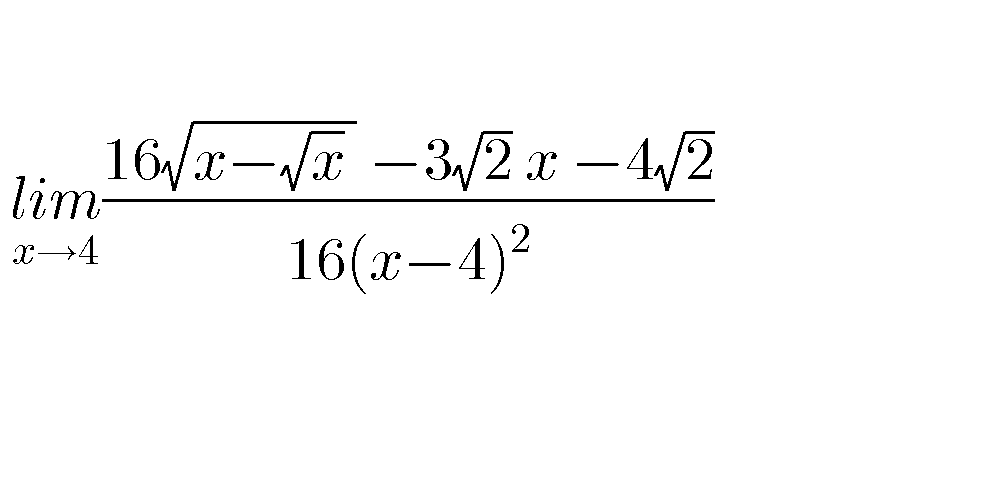
Commented by mathmax by abdo last updated on 23/Nov/19

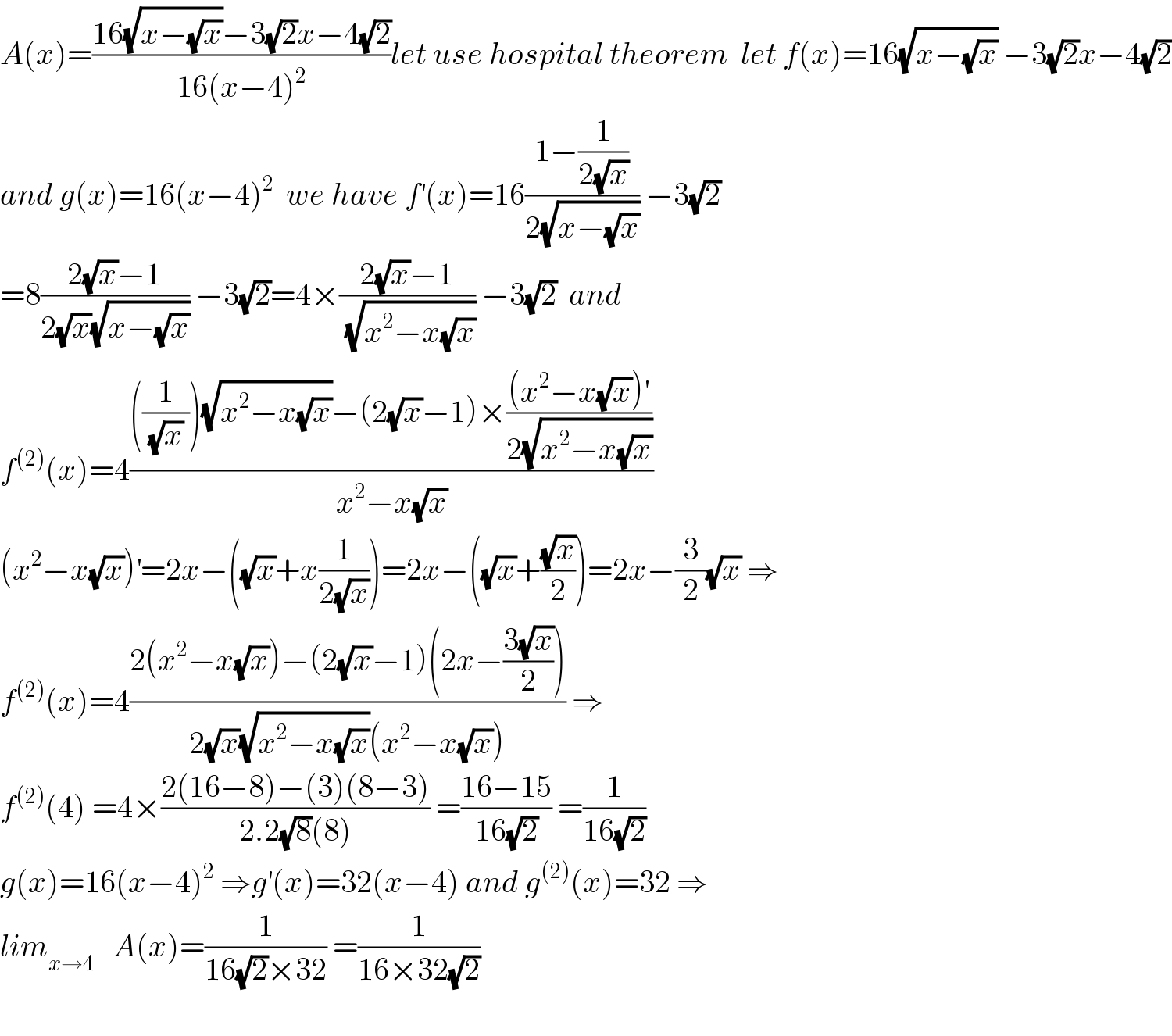
A(x)=((16(√(x−(√x)))−3(√2)x−4(√2))/(16(x−4)^2 ))let use hospital theorem let f(x)=16(√(x−(√x))) −3(√2)x−4(√2) and g(x)=16(x−4)^2 we have f^′ (x)=16((1−(1/(2(√x))))/(2(√(x−(√x))))) −3(√2) =8((2(√x)−1)/(2(√x)(√(x−(√x))))) −3(√2)=4×((2(√x)−1)/( (√(x^2 −x(√x))))) −3(√2) and f^((2)) (x)=4((((1/( (√x) )))(√(x^2 −x(√x)))−(2(√x)−1)×(((x^2 −x(√x))^′ )/(2(√(x^2 −x(√x))))))/(x^2 −x(√x))) (x^2 −x(√x))^′ =2x−((√x)+x(1/(2(√x))))=2x−((√x)+((√x)/2))=2x−(3/2)(√x) ⇒ f^((2)) (x)=4((2(x^2 −x(√x))−(2(√x)−1)(2x−((3(√x))/2)))/(2(√x)(√(x^2 −x(√x)))(x^2 −x(√x)))) ⇒ f^((2)) (4) =4×((2(16−8)−(3)(8−3))/(2.2(√8)(8))) =((16−15)/(16(√2))) =(1/(16(√2))) g(x)=16(x−4)^2 ⇒g^′ (x)=32(x−4) and g^((2)) (x)=32 ⇒ lim_(x→4) A(x)=(1/(16(√2)×32)) =(1/(16×32(√2)))

$${A}\left({x}\right)=\frac{\mathrm{16}\sqrt{{x}−\sqrt{{x}}}−\mathrm{3}\sqrt{\mathrm{2}}{x}−\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{16}\left({x}−\mathrm{4}\right)^{\mathrm{2}} }{let}\:{use}\:{hospital}\:{theorem}\:\:{let}\:{f}\left({x}\right)=\mathrm{16}\sqrt{{x}−\sqrt{{x}}}\:−\mathrm{3}\sqrt{\mathrm{2}}{x}−\mathrm{4}\sqrt{\mathrm{2}} \\ $$$${and}\:{g}\left({x}\right)=\mathrm{16}\left({x}−\mathrm{4}\right)^{\mathrm{2}} \:\:{we}\:{have}\:{f}^{'} \left({x}\right)=\mathrm{16}\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\mathrm{2}\sqrt{{x}−\sqrt{{x}}}}\:−\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$=\mathrm{8}\frac{\mathrm{2}\sqrt{{x}}−\mathrm{1}}{\mathrm{2}\sqrt{{x}}\sqrt{{x}−\sqrt{{x}}}}\:−\mathrm{3}\sqrt{\mathrm{2}}=\mathrm{4}×\frac{\mathrm{2}\sqrt{{x}}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −{x}\sqrt{{x}}}}\:−\mathrm{3}\sqrt{\mathrm{2}}\:\:{and}\: \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{4}\frac{\left(\frac{\mathrm{1}}{\:\sqrt{{x}}\:}\right)\sqrt{{x}^{\mathrm{2}} −{x}\sqrt{{x}}}−\left(\mathrm{2}\sqrt{{x}}−\mathrm{1}\right)×\frac{\left({x}^{\mathrm{2}} −{x}\sqrt{{x}}\right)^{'} }{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{x}\sqrt{{x}}}}}{{x}^{\mathrm{2}} −{x}\sqrt{{x}}} \\ $$$$\left({x}^{\mathrm{2}} −{x}\sqrt{{x}}\right)^{'} =\mathrm{2}{x}−\left(\sqrt{{x}}+{x}\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right)=\mathrm{2}{x}−\left(\sqrt{{x}}+\frac{\sqrt{{x}}}{\mathrm{2}}\right)=\mathrm{2}{x}−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}}\:\Rightarrow \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{4}\frac{\mathrm{2}\left({x}^{\mathrm{2}} −{x}\sqrt{{x}}\right)−\left(\mathrm{2}\sqrt{{x}}−\mathrm{1}\right)\left(\mathrm{2}{x}−\frac{\mathrm{3}\sqrt{{x}}}{\mathrm{2}}\right)}{\mathrm{2}\sqrt{{x}}\sqrt{{x}^{\mathrm{2}} −{x}\sqrt{{x}}}\left({x}^{\mathrm{2}} −{x}\sqrt{{x}}\right)}\:\Rightarrow \\ $$$${f}^{\left(\mathrm{2}\right)} \left(\mathrm{4}\right)\:=\mathrm{4}×\frac{\mathrm{2}\left(\mathrm{16}−\mathrm{8}\right)−\left(\mathrm{3}\right)\left(\mathrm{8}−\mathrm{3}\right)}{\mathrm{2}.\mathrm{2}\sqrt{\mathrm{8}}\left(\mathrm{8}\right)}\:=\frac{\mathrm{16}−\mathrm{15}}{\mathrm{16}\sqrt{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{16}\sqrt{\mathrm{2}}} \\ $$$${g}\left({x}\right)=\mathrm{16}\left({x}−\mathrm{4}\right)^{\mathrm{2}} \:\Rightarrow{g}^{'} \left({x}\right)=\mathrm{32}\left({x}−\mathrm{4}\right)\:{and}\:{g}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{32}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{4}} \:\:\:{A}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{16}\sqrt{\mathrm{2}}×\mathrm{32}}\:=\frac{\mathrm{1}}{\mathrm{16}×\mathrm{32}\sqrt{\mathrm{2}}} \\ $$$$ \\ $$

Commented by aliesam last updated on 23/Nov/19

$${god}\:{bless}\:{you}\:{sir}\:{thank}\:{you} \\ $$

Commented by mathmax by abdo last updated on 23/Nov/19

$${you}\:{are}\:{welcome}\:. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply