Menu Close

Question-74394

Tinku Tara 0 Comments
Pin




Question Number 74394 by aliesam last updated on 23/Nov/19
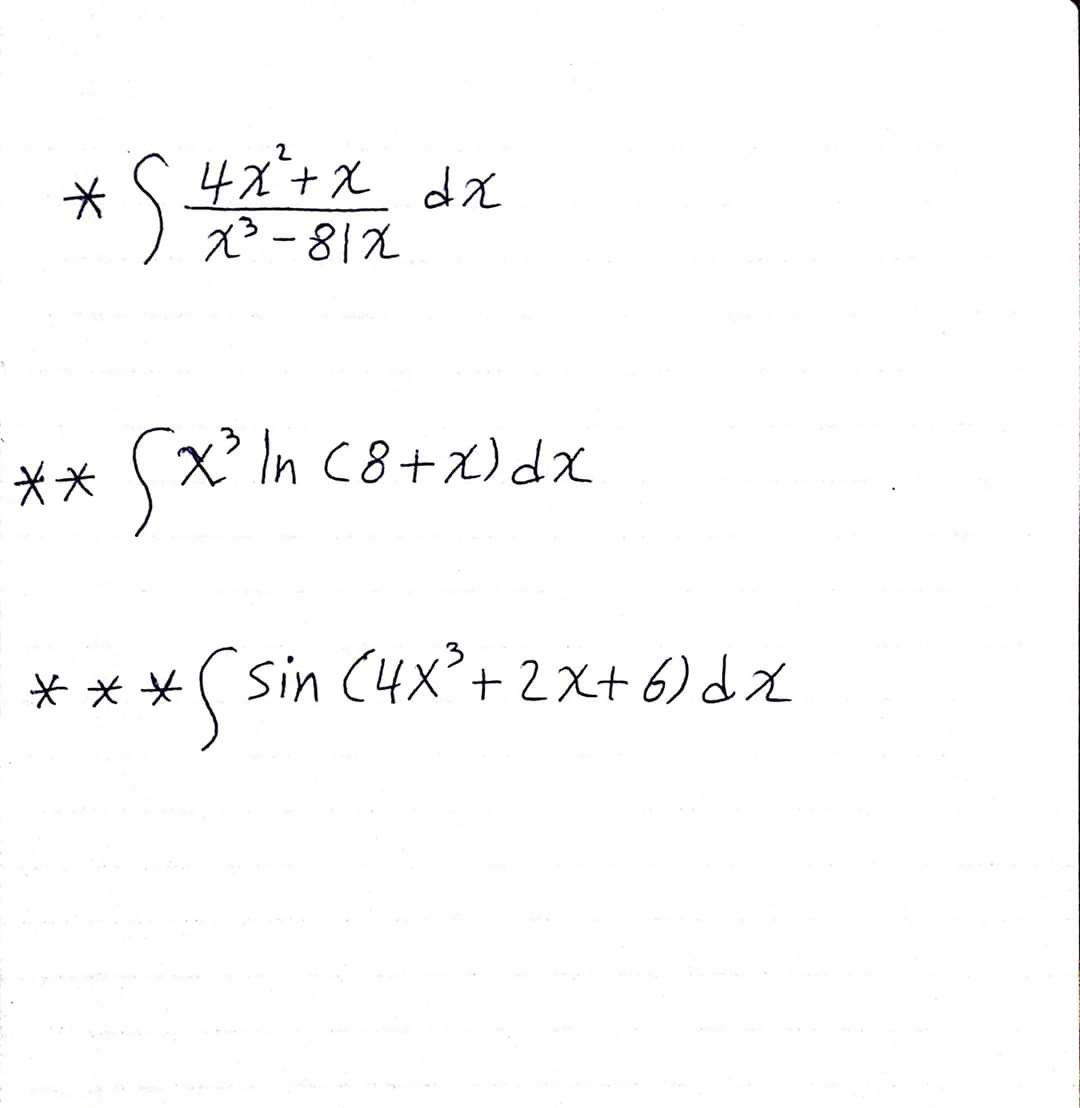
Commented by mathmax by abdo last updated on 23/Nov/19
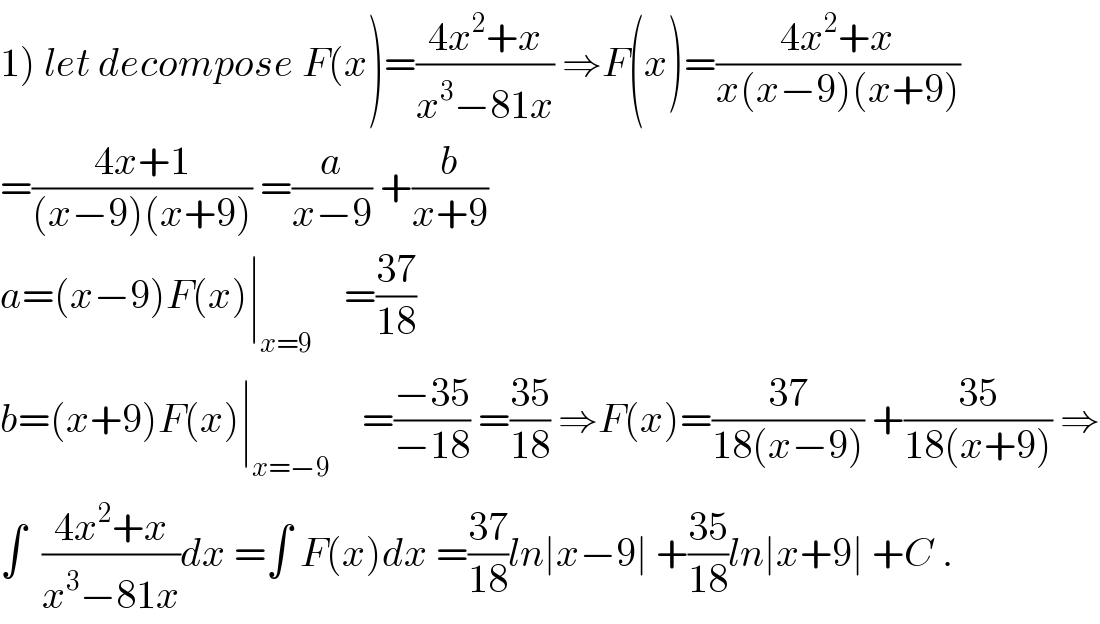
1) let decompose F(x)=((4x^2 +x)/(x^3 −81x)) ⇒F(x)=((4x^2 +x)/(x(x−9)(x+9))) =((4x+1)/((x−9)(x+9))) =(a/(x−9)) +(b/(x+9)) a=(x−9)F(x)∣_(x=9) =((37)/(18)) b=(x+9)F(x)∣_(x=−9) =((−35)/(−18)) =((35)/(18)) ⇒F(x)=((37)/(18(x−9))) +((35)/(18(x+9))) ⇒ ∫ ((4x^2 +x)/(x^3 −81x))dx =∫ F(x)dx =((37)/(18))ln∣x−9∣ +((35)/(18))ln∣x+9∣ +C .
$$\left.\mathrm{1}\right)\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{4}{x}^{\mathrm{2}} +{x}}{{x}^{\mathrm{3}} −\mathrm{81}{x}}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{4}{x}^{\mathrm{2}} +{x}}{{x}\left({x}−\mathrm{9}\right)\left({x}+\mathrm{9}\right)} \\ $$$$=\frac{\mathrm{4}{x}+\mathrm{1}}{\left({x}−\mathrm{9}\right)\left({x}+\mathrm{9}\right)}\:=\frac{{a}}{{x}−\mathrm{9}}\:+\frac{{b}}{{x}+\mathrm{9}} \\ $$$${a}=\left({x}−\mathrm{9}\right){F}\left({x}\right)\mid_{{x}=\mathrm{9}} \:\:\:\:=\frac{\mathrm{37}}{\mathrm{18}} \\ $$$${b}=\left({x}+\mathrm{9}\right){F}\left({x}\right)\mid_{{x}=−\mathrm{9}} \:\:\:\:=\frac{−\mathrm{35}}{−\mathrm{18}}\:=\frac{\mathrm{35}}{\mathrm{18}}\:\Rightarrow{F}\left({x}\right)=\frac{\mathrm{37}}{\mathrm{18}\left({x}−\mathrm{9}\right)}\:+\frac{\mathrm{35}}{\mathrm{18}\left({x}+\mathrm{9}\right)}\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{4}{x}^{\mathrm{2}} +{x}}{{x}^{\mathrm{3}} −\mathrm{81}{x}}{dx}\:=\int\:{F}\left({x}\right){dx}\:=\frac{\mathrm{37}}{\mathrm{18}}{ln}\mid{x}−\mathrm{9}\mid\:+\frac{\mathrm{35}}{\mathrm{18}}{ln}\mid{x}+\mathrm{9}\mid\:+{C}\:. \\ $$
Commented by mathmax by abdo last updated on 23/Nov/19
let A =∫ x^3 ln(x+8)dx ⇒A =_(x+8=t) ∫ (t−8)^3 ln(t)dt =∫ (t^3 +3 t^2 .8 +3t .8^2 +8^3 )ln(t)dt =∫ t^3 ln(t)dt +24 ∫ t^2 ln(t)dt + 192 ∫ t ln(t)dt +512 ∫ ln(t)dt ∫ lnt dt =tlnt −t +c_1 ∫ tln(t) dt =_(by psrts) (t^2 /2)lnt −∫(t^2 /2)(dt/t) =((t^2 lnt)/2)−(1/2)∫ tdt =((t^2 lnt)/2)−(t^2 /4) +c_2 ∫ t^2 ln(t)dt =((t^3 ln(t))/3)−∫(t^3 /3)(dt/t) =((t^3 ln(t))/3)−(1/3) ∫ t^(2 ) dt =((t^3 ln(t))/3)−(1/9)t^3 +c_3 ∫ t^3 ln(t)dt =((t^4 ln(t))/4) −∫ (t^4 /4) (dt/t) =((t^4 ln(t))/4)−(1/(16))t^4 +c_4 ⇒ A =(((x+8)^4 ln(x+8))/4)−(1/(16))(x+8)^4 +8(x+8)^3 ln(x+8)−(8/3)(x+8)^3 +192{ (((x+8)^2 ln(x+8))/2)−(((x+8)^2 )/4)}+512{(x+8)ln(x+8)−(x+8)} +C
$${let}\:{A}\:=\int\:{x}^{\mathrm{3}} {ln}\left({x}+\mathrm{8}\right){dx}\:\Rightarrow{A}\:=_{{x}+\mathrm{8}={t}} \:\:\int\:\:\left({t}−\mathrm{8}\right)^{\mathrm{3}} {ln}\left({t}\right){dt} \\ $$$$=\int\:\:\left({t}^{\mathrm{3}} \:+\mathrm{3}\:{t}^{\mathrm{2}} .\mathrm{8}\:+\mathrm{3}{t}\:.\mathrm{8}^{\mathrm{2}} \:+\mathrm{8}^{\mathrm{3}} \right){ln}\left({t}\right){dt} \\ $$$$=\int\:{t}^{\mathrm{3}} {ln}\left({t}\right){dt}\:+\mathrm{24}\:\int\:{t}^{\mathrm{2}} {ln}\left({t}\right){dt}\:+\:\mathrm{192}\:\int\:{t}\:{ln}\left({t}\right){dt}\:+\mathrm{512}\:\int\:{ln}\left({t}\right){dt} \\ $$$$\int\:{lnt}\:{dt}\:={tlnt}\:−{t}\:+{c}_{\mathrm{1}} \\ $$$$\int\:{tln}\left({t}\right)\:{dt}\:=_{{by}\:{psrts}} \:\:\frac{{t}^{\mathrm{2}} }{\mathrm{2}}{lnt}\:−\int\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\frac{{dt}}{{t}}\:=\frac{{t}^{\mathrm{2}} {lnt}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\:{tdt} \\ $$$$=\frac{{t}^{\mathrm{2}} {lnt}}{\mathrm{2}}−\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\:+{c}_{\mathrm{2}} \\ $$$$\int\:{t}^{\mathrm{2}} {ln}\left({t}\right){dt}\:=\frac{{t}^{\mathrm{3}} {ln}\left({t}\right)}{\mathrm{3}}−\int\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\frac{{dt}}{{t}}\:=\frac{{t}^{\mathrm{3}} {ln}\left({t}\right)}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\:\int\:{t}^{\mathrm{2}\:} {dt} \\ $$$$=\frac{{t}^{\mathrm{3}} {ln}\left({t}\right)}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{9}}{t}^{\mathrm{3}} \:+{c}_{\mathrm{3}} \\ $$$$\int\:{t}^{\mathrm{3}} {ln}\left({t}\right){dt}\:=\frac{{t}^{\mathrm{4}} {ln}\left({t}\right)}{\mathrm{4}}\:−\int\:\frac{{t}^{\mathrm{4}} }{\mathrm{4}}\:\frac{{dt}}{{t}}\:=\frac{{t}^{\mathrm{4}} {ln}\left({t}\right)}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{16}}{t}^{\mathrm{4}} \:\:+{c}_{\mathrm{4}} \:\Rightarrow \\ $$$${A}\:=\frac{\left({x}+\mathrm{8}\right)^{\mathrm{4}} {ln}\left({x}+\mathrm{8}\right)}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{16}}\left({x}+\mathrm{8}\right)^{\mathrm{4}} \:+\mathrm{8}\left({x}+\mathrm{8}\right)^{\mathrm{3}} {ln}\left({x}+\mathrm{8}\right)−\frac{\mathrm{8}}{\mathrm{3}}\left({x}+\mathrm{8}\right)^{\mathrm{3}} \\ $$$$+\mathrm{192}\left\{\:\frac{\left({x}+\mathrm{8}\right)^{\mathrm{2}} {ln}\left({x}+\mathrm{8}\right)}{\mathrm{2}}−\frac{\left({x}+\mathrm{8}\right)^{\mathrm{2}} }{\mathrm{4}}\right\}+\mathrm{512}\left\{\left({x}+\mathrm{8}\right){ln}\left({x}+\mathrm{8}\right)−\left({x}+\mathrm{8}\right)\right\}\:+{C} \\ $$
Commented by ~blr237~ last updated on 23/Nov/19
f(x)=∫x^3 ln(8+x)dx by part we have u′=x^3 → u=(1/4)x^4 −(8^4 /4) and v=ln(8+x) → v′=(1/(8+x)) f(x)=[(((x^4 −8^4 )/4))ln(8+x)]−(1/4)∫^ ((x^4 −8^4 )/(x−(−8)))dx = (((x^4 −8^4 )/4))ln(8+x) −(1/4)∫ (8^4 /8)[1+(−(x/8))+(−(x/8))^2 +(((−x)/8))^3 dx =(((x^4 −8^4 )/4))ln(8+x)−4^5 [x−(x^2 /(16))+(x^3 /(3×64))−(x^4 /(4×8^3 ))]+c So f(x)=(((x^4 −8^4 )/4))ln(8+x)−4^5 x+4^3 x^2 −((4^2 x^3 )/3)+(x^4 /4)+c
$${f}\left({x}\right)=\int{x}^{\mathrm{3}} {ln}\left(\mathrm{8}+{x}\right){dx} \\ $$$$\:{by}\:\:{part}\:\:{we}\:{have}\:\:{u}'={x}^{\mathrm{3}} \:\:\:\rightarrow\:{u}=\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} −\frac{\mathrm{8}^{\mathrm{4}} }{\mathrm{4}} \\ $$$${and}\:\:{v}={ln}\left(\mathrm{8}+{x}\right)\:\rightarrow\:{v}'=\frac{\mathrm{1}}{\mathrm{8}+{x}}\: \\ $$$${f}\left({x}\right)=\left[\left(\frac{{x}^{\mathrm{4}} −\mathrm{8}^{\mathrm{4}} }{\mathrm{4}}\right){ln}\left(\mathrm{8}+{x}\right)\right]−\frac{\mathrm{1}}{\mathrm{4}}\int^{} \:\frac{{x}^{\mathrm{4}} −\mathrm{8}^{\mathrm{4}} }{{x}−\left(−\mathrm{8}\right)}{dx}\: \\ $$$$=\:\left(\frac{{x}^{\mathrm{4}} −\mathrm{8}^{\mathrm{4}} }{\mathrm{4}}\right){ln}\left(\mathrm{8}+{x}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{8}^{\mathrm{4}} }{\mathrm{8}}\left[\mathrm{1}+\left(−\frac{{x}}{\mathrm{8}}\right)+\left(−\frac{{x}}{\mathrm{8}}\right)^{\mathrm{2}} +\left(\frac{−{x}}{\mathrm{8}}\right)^{\mathrm{3}} {dx}\right. \\ $$$$=\left(\frac{{x}^{\mathrm{4}} −\mathrm{8}^{\mathrm{4}} }{\mathrm{4}}\right){ln}\left(\mathrm{8}+{x}\right)−\mathrm{4}^{\mathrm{5}} \left[{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{16}}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}×\mathrm{64}}−\frac{{x}^{\mathrm{4}} }{\mathrm{4}×\mathrm{8}^{\mathrm{3}} }\right]+{c} \\ $$$${So}\:\: \\ $$$${f}\left({x}\right)=\left(\frac{{x}^{\mathrm{4}} −\mathrm{8}^{\mathrm{4}} }{\mathrm{4}}\right){ln}\left(\mathrm{8}+{x}\right)−\mathrm{4}^{\mathrm{5}} {x}+\mathrm{4}^{\mathrm{3}} {x}^{\mathrm{2}} −\frac{\mathrm{4}^{\mathrm{2}} {x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+{c} \\ $$$$ \\ $$
Commented by MJS last updated on 24/Nov/19
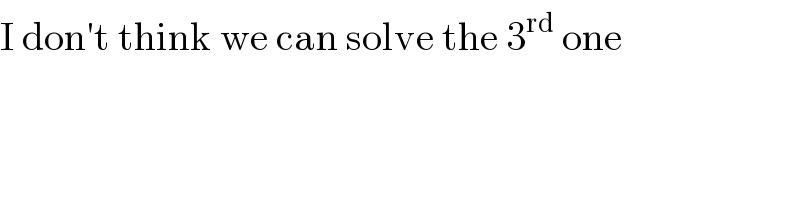
I don′t think we can solve the 3^(rd) one
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{one} \\ $$
Answered by MJS last updated on 23/Nov/19
∗ ∫((4x^2 +x)/(x^3 −81x))dx=∫((4x+1)/(x^2 −81))dx= =((37)/(18))∫(dx/(x−9))+((35)/(18))∫(dx/(x+9))= =((37)/(18))ln (x−9) +((35)/(18))ln (x+9) +C ∗∗ ∫x^3 ln (x+8) dx= [u′=x^3 ⇒ u=(1/4)x^4 ; v=ln (x+8) ⇒ v′=(1/(x+8))] =(1/4)x^4 ln (x+8) −(1/4)∫(x^4 /(x+8))dx= ∫(x^4 /(x+8))dx=∫(x^3 −8x^2 +64x−512+((4096)/(x+8)))dx= =(1/4)x^4 −(8/3)x^3 +32x^2 −512x+4096ln (x+8) =−((x(3x^3 −32x^2 +384x−6144))/(48))+((1/4)x^4 −1024)ln (x+8) +C
$$\ast \\ $$$$\int\frac{\mathrm{4}{x}^{\mathrm{2}} +{x}}{{x}^{\mathrm{3}} −\mathrm{81}{x}}{dx}=\int\frac{\mathrm{4}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{81}}{dx}= \\ $$$$=\frac{\mathrm{37}}{\mathrm{18}}\int\frac{{dx}}{{x}−\mathrm{9}}+\frac{\mathrm{35}}{\mathrm{18}}\int\frac{{dx}}{{x}+\mathrm{9}}= \\ $$$$=\frac{\mathrm{37}}{\mathrm{18}}\mathrm{ln}\:\left({x}−\mathrm{9}\right)\:+\frac{\mathrm{35}}{\mathrm{18}}\mathrm{ln}\:\left({x}+\mathrm{9}\right)\:+{C} \\ $$$$ \\ $$$$\ast\ast \\ $$$$\int{x}^{\mathrm{3}} \mathrm{ln}\:\left({x}+\mathrm{8}\right)\:{dx}= \\ $$$$\:\:\:\:\:\left[{u}'={x}^{\mathrm{3}} \:\Rightarrow\:{u}=\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} ;\:{v}=\mathrm{ln}\:\left({x}+\mathrm{8}\right)\:\Rightarrow\:{v}'=\frac{\mathrm{1}}{{x}+\mathrm{8}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} \mathrm{ln}\:\left({x}+\mathrm{8}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}\int\frac{{x}^{\mathrm{4}} }{{x}+\mathrm{8}}{dx}= \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{{x}^{\mathrm{4}} }{{x}+\mathrm{8}}{dx}=\int\left({x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{64}{x}−\mathrm{512}+\frac{\mathrm{4096}}{{x}+\mathrm{8}}\right){dx}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} −\frac{\mathrm{8}}{\mathrm{3}}{x}^{\mathrm{3}} +\mathrm{32}{x}^{\mathrm{2}} −\mathrm{512}{x}+\mathrm{4096ln}\:\left({x}+\mathrm{8}\right) \\ $$$$ \\ $$$$=−\frac{{x}\left(\mathrm{3}{x}^{\mathrm{3}} −\mathrm{32}{x}^{\mathrm{2}} +\mathrm{384}{x}−\mathrm{6144}\right)}{\mathrm{48}}+\left(\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{4}} −\mathrm{1024}\right)\mathrm{ln}\:\left({x}+\mathrm{8}\right)\:+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *