Question Number 74415 by Learner-123 last updated on 24/Nov/19
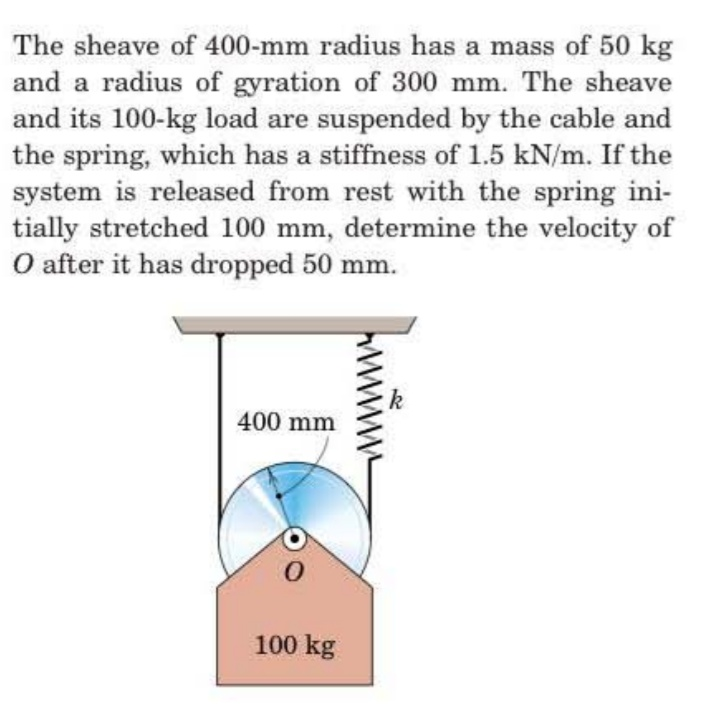
Commented by Learner-123 last updated on 24/Nov/19
$${please}\:{solve}\:{this}\:{by}\:{conservation}\:{of} \\ $$$${energy}. \\ $$
Answered by ajfour last updated on 24/Nov/19
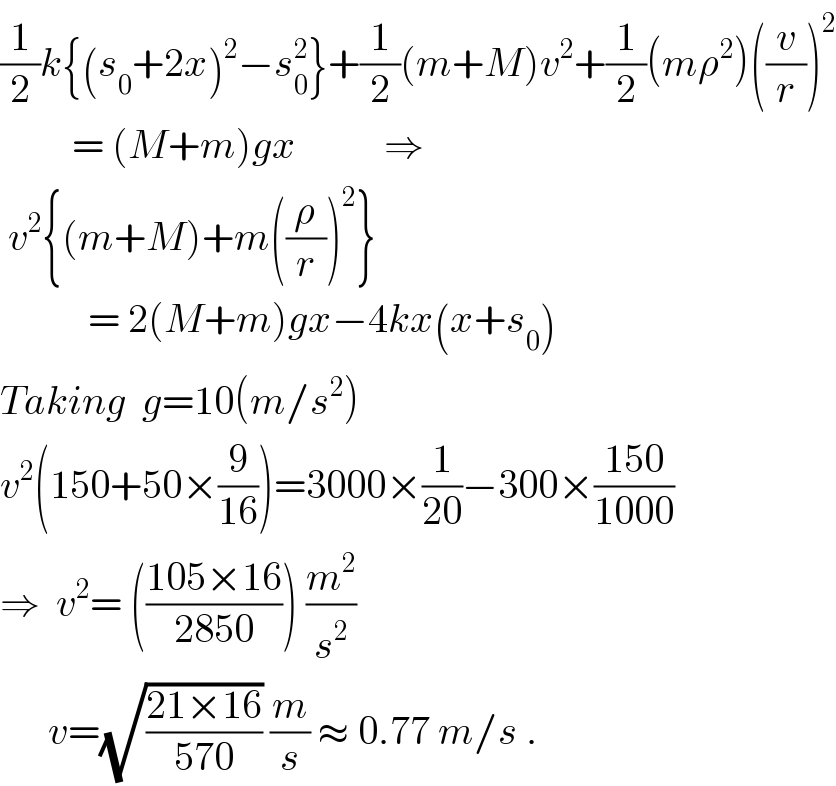
$$\frac{\mathrm{1}}{\mathrm{2}}{k}\left\{\left({s}_{\mathrm{0}} +\mathrm{2}{x}\right)^{\mathrm{2}} −{s}_{\mathrm{0}} ^{\mathrm{2}} \right\}+\frac{\mathrm{1}}{\mathrm{2}}\left({m}+{M}\right){v}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left({m}\rho^{\mathrm{2}} \right)\left(\frac{{v}}{{r}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\left({M}+{m}\right){gx}\:\:\:\:\:\:\:\:\:\:\:\Rightarrow \\ $$$$\:{v}^{\mathrm{2}} \left\{\left({m}+{M}\right)+{m}\left(\frac{\rho}{{r}}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\left({M}+{m}\right){gx}−\mathrm{4}{kx}\left({x}+{s}_{\mathrm{0}} \right) \\ $$$${Taking}\:\:{g}=\mathrm{10}\left({m}/{s}^{\mathrm{2}} \right) \\ $$$${v}^{\mathrm{2}} \left(\mathrm{150}+\mathrm{50}×\frac{\mathrm{9}}{\mathrm{16}}\right)=\mathrm{3000}×\frac{\mathrm{1}}{\mathrm{20}}−\mathrm{300}×\frac{\mathrm{150}}{\mathrm{1000}} \\ $$$$\Rightarrow\:\:{v}^{\mathrm{2}} =\:\left(\frac{\mathrm{105}×\mathrm{16}}{\mathrm{2850}}\right)\:\frac{{m}^{\mathrm{2}} }{{s}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:{v}=\sqrt{\frac{\mathrm{21}×\mathrm{16}}{\mathrm{570}}}\:\frac{{m}}{{s}}\:\approx\:\mathrm{0}.\mathrm{77}\:{m}/{s}\:. \\ $$
Commented by Learner-123 last updated on 24/Nov/19

$${thanks}\:{sir}! \\ $$
