Question-74456

Question Number 74456 by liki last updated on 24/Nov/19

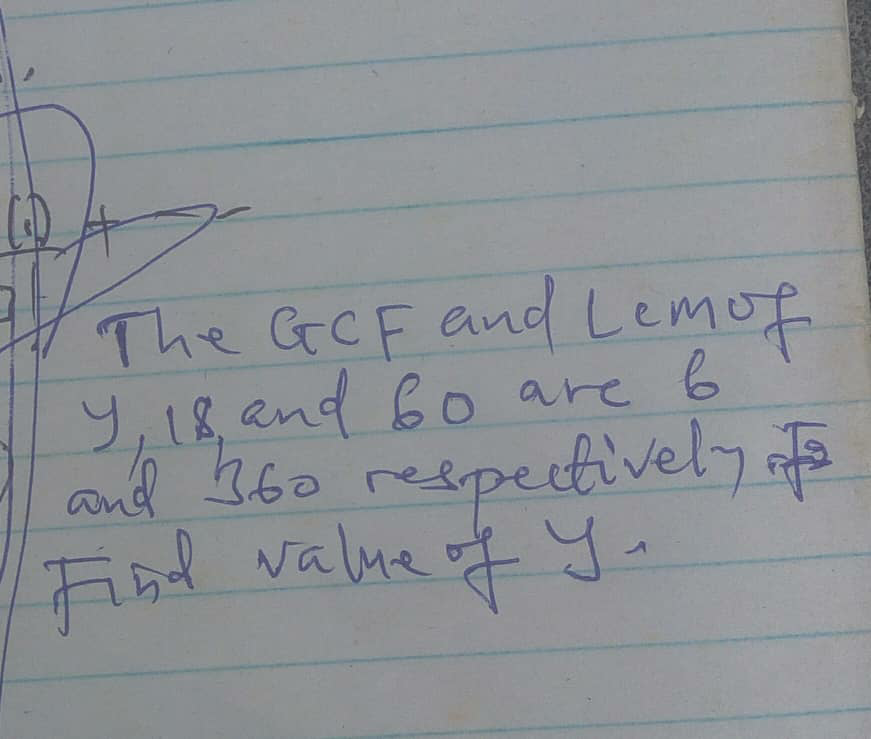
Commented by liki last updated on 24/Nov/19

$$…{plz}\:{anyone}\:{knowing}\:{simple}\:{logic}\:{of} \\ $$$${find}\:{the}\:{possible}\:{number},{because}\: \\ $$$$\:{this}\:{always}\:{i}\:{did}\:{not}\:{understand}\:{so}\:{pl}\: \\ $$$$\:{i}\:{need}\:{simple}\:{way}\:{of}\:{find}\:{the}\:{others}\:{no}. \\ $$

Commented by $@ty@m123 last updated on 24/Nov/19

$${there}\:{is}\:{no}\:{hard}\:{and}\:{fast}\:{rule}. \\ $$$${Logic}\:\&\:{method}\:{of}\:{solving}\:{problem} \\ $$$${may}\:{vary}\:{from}\:{question}\:{to}\:{question}. \\ $$$${You}\:{can}\:{learn}\:{this}\:{only}\: \\ $$$${through}\:{practice}. \\ $$

Answered by mr W last updated on 24/Nov/19

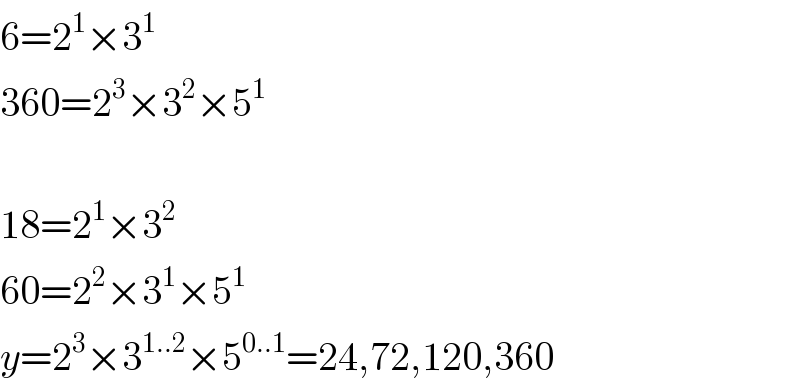
6=2^1 ×3^1 360=2^3 ×3^2 ×5^1 18=2^1 ×3^2 60=2^2 ×3^1 ×5^1 y=2^3 ×3^(1..2) ×5^(0..1) =24,72,120,360

$$\mathrm{6}=\mathrm{2}^{\mathrm{1}} ×\mathrm{3}^{\mathrm{1}} \\ $$$$\mathrm{360}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{18}=\mathrm{2}^{\mathrm{1}} ×\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{60}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{1}} ×\mathrm{5}^{\mathrm{1}} \\ $$$${y}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{1}..\mathrm{2}} ×\mathrm{5}^{\mathrm{0}..\mathrm{1}} =\mathrm{24},\mathrm{72},\mathrm{120},\mathrm{360} \\ $$

Commented by liki last updated on 24/Nov/19

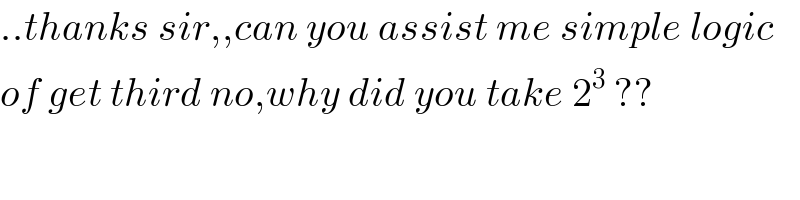
..thanks sir,,can you assist me simple logic of get third no,why did you take 2^3 ??

$$..{thanks}\:{sir},,{can}\:{you}\:{assist}\:{me}\:{simple}\:{logic}\: \\ $$$${of}\:{get}\:{third}\:{no},{why}\:{did}\:{you}\:{take}\:\mathrm{2}^{\mathrm{3}} \:?? \\ $$

Commented by mr W last updated on 24/Nov/19

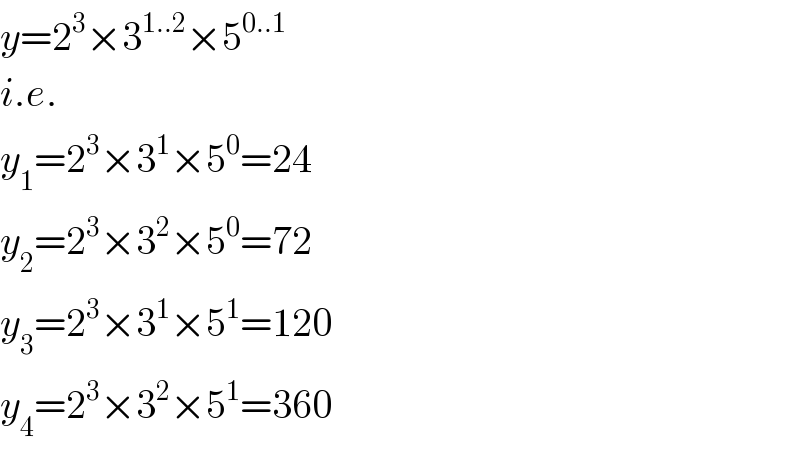
y=2^3 ×3^(1..2) ×5^(0..1) i.e. y_1 =2^3 ×3^1 ×5^0 =24 y_2 =2^3 ×3^2 ×5^0 =72 y_3 =2^3 ×3^1 ×5^1 =120 y_4 =2^3 ×3^2 ×5^1 =360

$${y}=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{1}..\mathrm{2}} ×\mathrm{5}^{\mathrm{0}..\mathrm{1}} \\ $$$${i}.{e}. \\ $$$${y}_{\mathrm{1}} =\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{1}} ×\mathrm{5}^{\mathrm{0}} =\mathrm{24} \\ $$$${y}_{\mathrm{2}} =\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{0}} =\mathrm{72} \\ $$$${y}_{\mathrm{3}} =\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{1}} ×\mathrm{5}^{\mathrm{1}} =\mathrm{120} \\ $$$${y}_{\mathrm{4}} =\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} ×\mathrm{5}^{\mathrm{1}} =\mathrm{360} \\ $$

Commented by liki last updated on 24/Nov/19

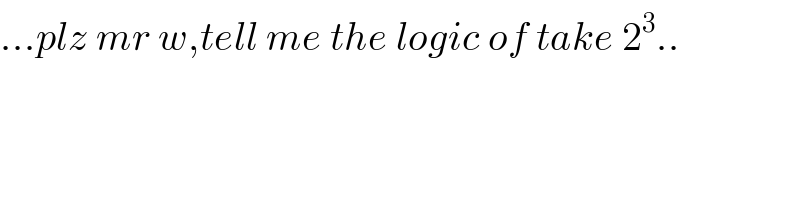
...plz mr w,tell me the logic of take 2^3 ..

$$…{plz}\:{mr}\:{w},{tell}\:{me}\:{the}\:{logic}\:{of}\:{take}\:\mathrm{2}^{\mathrm{3}} .. \\ $$

Commented by mr W last updated on 24/Nov/19

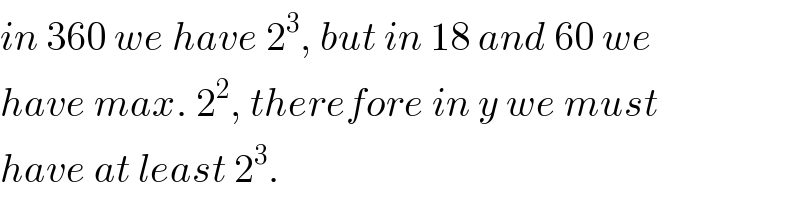
in 360 we have 2^3 , but in 18 and 60 we have max. 2^2 , therefore in y we must have at least 2^3 .

$${in}\:\mathrm{360}\:{we}\:{have}\:\mathrm{2}^{\mathrm{3}} ,\:{but}\:{in}\:\mathrm{18}\:{and}\:\mathrm{60}\:{we} \\ $$$${have}\:{max}.\:\mathrm{2}^{\mathrm{2}} ,\:{therefore}\:{in}\:{y}\:{we}\:{must} \\ $$$${have}\:{at}\:{least}\:\mathrm{2}^{\mathrm{3}} . \\ $$

Commented by liki last updated on 24/Nov/19

$$..{Thank}\:{you}\:{so}\:{much}\:{sir}\:{be}\:{blesed} \\ $$

Commented by liki last updated on 24/Nov/19

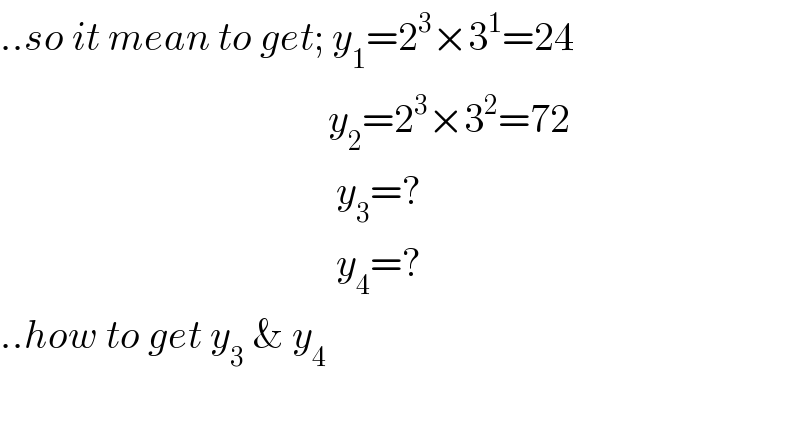
..so it mean to get; y_1 =2^3 ×3^1 =24 y_2 =2^3 ×3^2 =72 y_3 =? y_4 =? ..how to get y_3 & y_4

$$..{so}\:{it}\:{mean}\:{to}\:{get};\:{y}_{\mathrm{1}} =\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{1}} =\mathrm{24} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}_{\mathrm{2}} =\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{2}} =\mathrm{72} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}_{\mathrm{3}} =? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}_{\mathrm{4}} =? \\ $$$$..{how}\:{to}\:{get}\:{y}_{\mathrm{3}} \:\&\:{y}_{\mathrm{4}} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply