Question Number 74473 by arkanmath7@gmail.com last updated on 24/Nov/19

Commented by mathmax by abdo last updated on 24/Nov/19
![∣z−1∣=1 ⇒z−1=e^(iθ) 0≤θ≤π ⇒z=1+e^(iθ) ∫_C (z^− )^2 dz =∫_0 ^(2π) (1+e^(−iθ) )^2 i e^(iθ) dθ =i ∫_0 ^(2π) (1+2e^(−iθ) +e^(−2iθ) )e^(iθ) dθ =i ∫_0 ^(2π) (e^(iθ) +2 +e^(−iθ) )dθ =i ∫_0 ^(2π) (e^(iθ) +e^(−iθ) )dθ +2i∫_0 ^(2π) dθ =2i ∫_0 ^(2π) cosθ dθ +4iπ =2i[sinθ]_0 ^(2π) +4iπ =0 +4iπ =4iπ](https://www.tinkutara.com/question/Q74489.png)
$$\mid{z}−\mathrm{1}\mid=\mathrm{1}\:\Rightarrow{z}−\mathrm{1}={e}^{{i}\theta} \:\:\:\:\mathrm{0}\leqslant\theta\leqslant\pi\:\Rightarrow{z}=\mathrm{1}+{e}^{{i}\theta} \\ $$$$\int_{{C}} \left(\overset{−} {{z}}\right)^{\mathrm{2}} {dz}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\left(\mathrm{1}+{e}^{−{i}\theta} \right)^{\mathrm{2}} {i}\:{e}^{{i}\theta} \:{d}\theta\: \\ $$$$={i}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{1}+\mathrm{2}{e}^{−{i}\theta} \:+{e}^{−\mathrm{2}{i}\theta} \right){e}^{{i}\theta} \:{d}\theta \\ $$$$={i}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left({e}^{{i}\theta} \:+\mathrm{2}\:\:+{e}^{−{i}\theta} \right){d}\theta\:\:={i}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left({e}^{{i}\theta} \:+{e}^{−{i}\theta} \right){d}\theta\:\:+\mathrm{2}{i}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{d}\theta \\ $$$$=\mathrm{2}{i}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{cos}\theta\:{d}\theta\:\:+\mathrm{4}{i}\pi\:=\mathrm{2}{i}\left[{sin}\theta\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \:+\mathrm{4}{i}\pi\:=\mathrm{0}\:+\mathrm{4}{i}\pi\:=\mathrm{4}{i}\pi \\ $$
Commented by mathmax by abdo last updated on 24/Nov/19
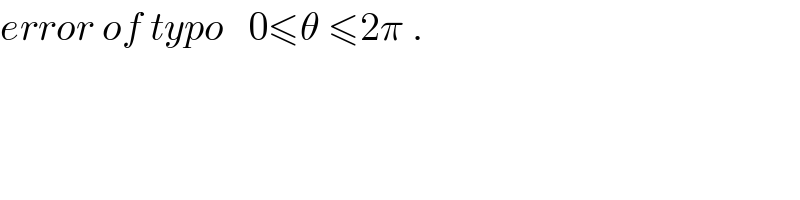
$${error}\:{of}\:{typo}\:\:\:\mathrm{0}\leqslant\theta\:\leqslant\mathrm{2}\pi\:. \\ $$
Answered by mind is power last updated on 24/Nov/19
![{z∈C,∣z−1∣=1}={1+e^(it) ,t∈[0,2π]} ∫_C z^2^− dz=∫_0 ^(2π) (1+e^(−it) )^2 .ie^(it) dt =∫i(1+e^(−2it) +2e^(−it) )e^(it) dt =i∫_0 ^(2π) (e^(it) +e^(−it) +2)dt =4iπ](https://www.tinkutara.com/question/Q74477.png)
$$\left\{{z}\in\mathbb{C},\mid{z}−\mathrm{1}\mid=\mathrm{1}\right\}=\left\{\mathrm{1}+{e}^{{it}} ,{t}\in\left[\mathrm{0},\mathrm{2}\pi\right]\right\} \\ $$$$\int_{{C}} {z}^{\overset{−} {\mathrm{2}}} {dz}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{1}+{e}^{−{it}} \right)^{\mathrm{2}} .{ie}^{{it}} {dt} \\ $$$$=\int{i}\left(\mathrm{1}+{e}^{−\mathrm{2}{it}} +\mathrm{2}{e}^{−{it}} \right){e}^{{it}} {dt} \\ $$$$={i}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left({e}^{{it}} +{e}^{−{it}} +\mathrm{2}\right){dt} \\ $$$$=\mathrm{4}{i}\pi \\ $$
Commented by arkanmath7@gmail.com last updated on 24/Nov/19
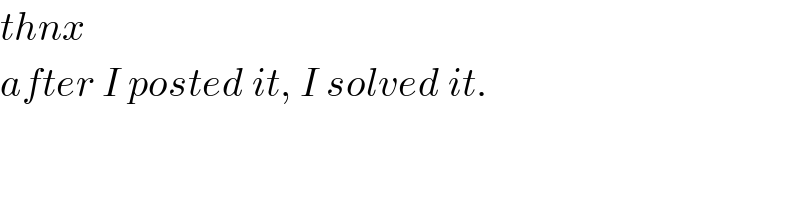
$${thnx}\: \\ $$$${after}\:{I}\:{posted}\:{it},\:{I}\:{solved}\:{it}. \\ $$
