Question-74483

Question Number 74483 by liki last updated on 24/Nov/19

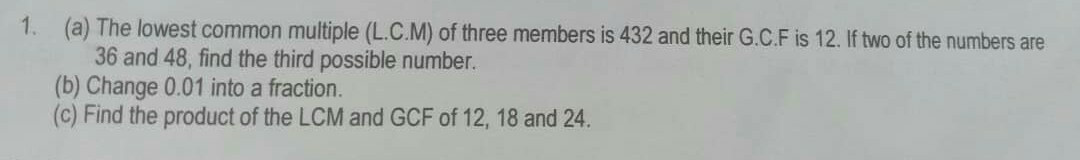
Commented by liki last updated on 24/Nov/19

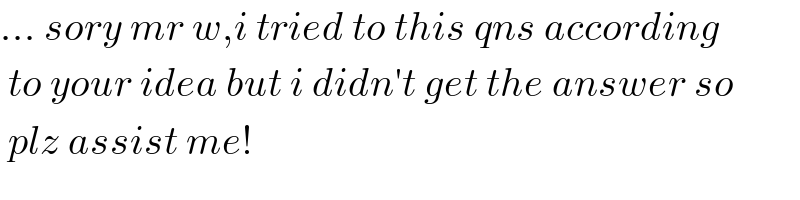
$$…\:{sory}\:{mr}\:{w},{i}\:{tried}\:{to}\:{this}\:{qns}\:{according} \\ $$$$\:{to}\:{your}\:{idea}\:{but}\:{i}\:{didn}'{t}\:{get}\:{the}\:{answer}\:{so}\: \\ $$$$\:{plz}\:{assist}\:{me}! \\ $$

Commented by liki last updated on 24/Nov/19

$${Qn}\:\mathrm{1}\left({a}\right) \\ $$

Answered by mr W last updated on 24/Nov/19

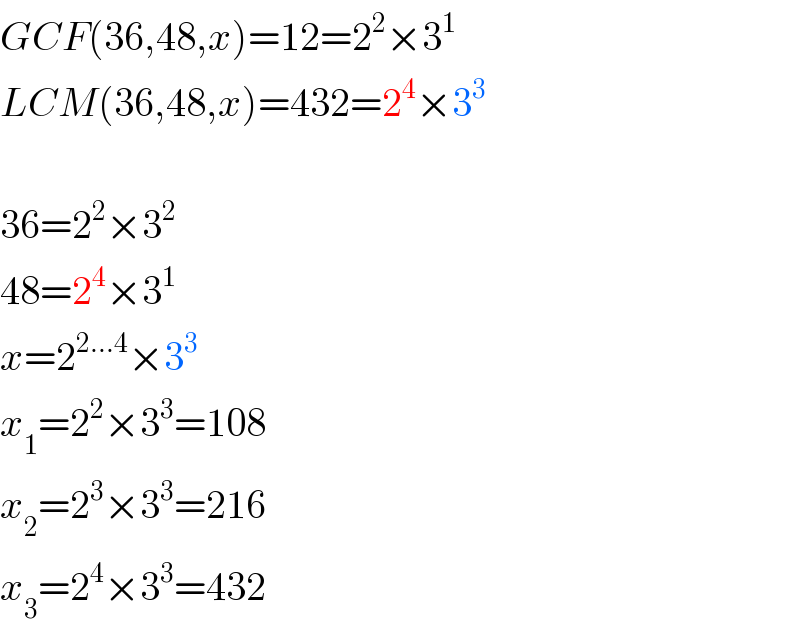
GCF(36,48,x)=12=2^2 ×3^1 LCM(36,48,x)=432=2^4 ×3^3 36=2^2 ×3^2 48=2^4 ×3^1 x=2^(2...4) ×3^3 x_1 =2^2 ×3^3 =108 x_2 =2^3 ×3^3 =216 x_3 =2^4 ×3^3 =432

$${GCF}\left(\mathrm{36},\mathrm{48},{x}\right)=\mathrm{12}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{1}} \\ $$$${LCM}\left(\mathrm{36},\mathrm{48},{x}\right)=\mathrm{432}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{36}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{2}} \\ $$$$\mathrm{48}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{1}} \\ $$$${x}=\mathrm{2}^{\mathrm{2}…\mathrm{4}} ×\mathrm{3}^{\mathrm{3}} \\ $$$${x}_{\mathrm{1}} =\mathrm{2}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{3}} =\mathrm{108} \\ $$$${x}_{\mathrm{2}} =\mathrm{2}^{\mathrm{3}} ×\mathrm{3}^{\mathrm{3}} =\mathrm{216} \\ $$$${x}_{\mathrm{3}} =\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{3}} =\mathrm{432} \\ $$

Commented by mr W last updated on 24/Nov/19

explanation how i solve: (it should be easy to understand, when you know what are LCM and GCF) GCF(36,48,x)=12=2^2 ×3^1 each factor here (2^2 and 3^1 ) must be included in each number, i.e. x=2^(≥2) ×3^(≥1) ...(i) LCM(36,48,x)=432=2^4 ×3^3 they are the largest allowable factors in all numbers and each factor here (2^4 and 3^3 ) must be included at least in one number, 2^4 is already in 48, but 3^3 is not in 48 and 36, thus it must be in x, i.e. x=2^(≤4) ×3^3 ...(ii) from (i) and (ii): ⇒x=2^(2...4) ×3^3

$${explanation}\:{how}\:{i}\:{solve}: \\ $$$$\left({it}\:{should}\:{be}\:{easy}\:{to}\:{understand},\:{when}\right. \\ $$$$\left.{you}\:{know}\:{what}\:{are}\:{LCM}\:{and}\:{GCF}\right) \\ $$$$ \\ $$$${GCF}\left(\mathrm{36},\mathrm{48},{x}\right)=\mathrm{12}=\mathrm{2}^{\mathrm{2}} ×\mathrm{3}^{\mathrm{1}} \\ $$$${each}\:{factor}\:{here}\:\left(\mathrm{2}^{\mathrm{2}} \:{and}\:\mathrm{3}^{\mathrm{1}} \right)\:{must}\:{be} \\ $$$${included}\:{in}\:{each}\:{number},\:{i}.{e}. \\ $$$${x}=\mathrm{2}^{\geqslant\mathrm{2}} ×\mathrm{3}^{\geqslant\mathrm{1}} \:\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${LCM}\left(\mathrm{36},\mathrm{48},{x}\right)=\mathrm{432}=\mathrm{2}^{\mathrm{4}} ×\mathrm{3}^{\mathrm{3}} \\ $$$${they}\:{are}\:{the}\:{largest}\:{allowable}\:{factors} \\ $$$${in}\:{all}\:{numbers}\:{and}\: \\ $$$${each}\:{factor}\:{here}\:\left(\mathrm{2}^{\mathrm{4}} \:{and}\:\mathrm{3}^{\mathrm{3}} \right)\:{must}\:{be} \\ $$$${included}\:{at}\:{least}\:{in}\:{one}\:{number}, \\ $$$$\mathrm{2}^{\mathrm{4}} \:{is}\:{already}\:{in}\:\mathrm{48},\:{but}\:\mathrm{3}^{\mathrm{3}} \:{is}\:{not}\:{in} \\ $$$$\mathrm{48}\:{and}\:\mathrm{36},\:{thus}\:{it}\:{must}\:{be}\:{in}\:{x},\:{i}.{e}. \\ $$$${x}=\mathrm{2}^{\leqslant\mathrm{4}} ×\mathrm{3}^{\mathrm{3}} \:\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right): \\ $$$$\Rightarrow{x}=\mathrm{2}^{\mathrm{2}…\mathrm{4}} ×\mathrm{3}^{\mathrm{3}} \\ $$

Commented by liki last updated on 25/Nov/19

$$…{Thank}\:{you}\:{sir},,{very}\:{technical}\:{question} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply