Question Number 74527 by Maclaurin Stickker last updated on 25/Nov/19
Commented by Maclaurin Stickker last updated on 25/Nov/19

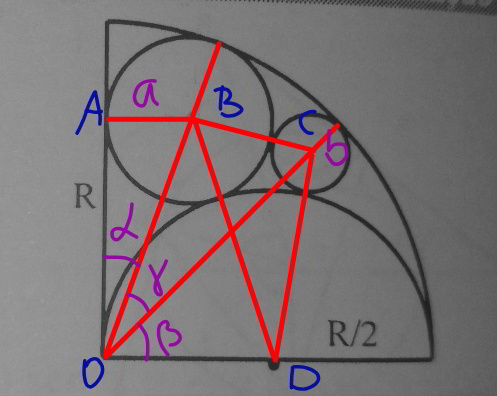
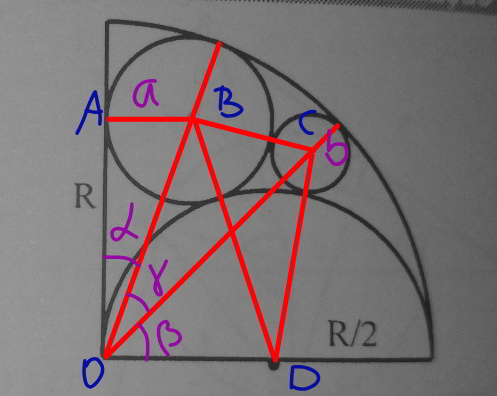
$${In}\:{the}\:{figure}\:{determine}\:{the}\:{radius} \\ $$$${of}\:{the}\:{smallest}\:{circumference}\:{as}\:{a} \\ $$$${function}\:{of}\:{the}\:{radius}\:\boldsymbol{\mathrm{R}}\:{of}\:{the}\:{quadrant}. \\ $$
Answered by ajfour last updated on 25/Nov/19
Commented by ajfour last updated on 25/Nov/19
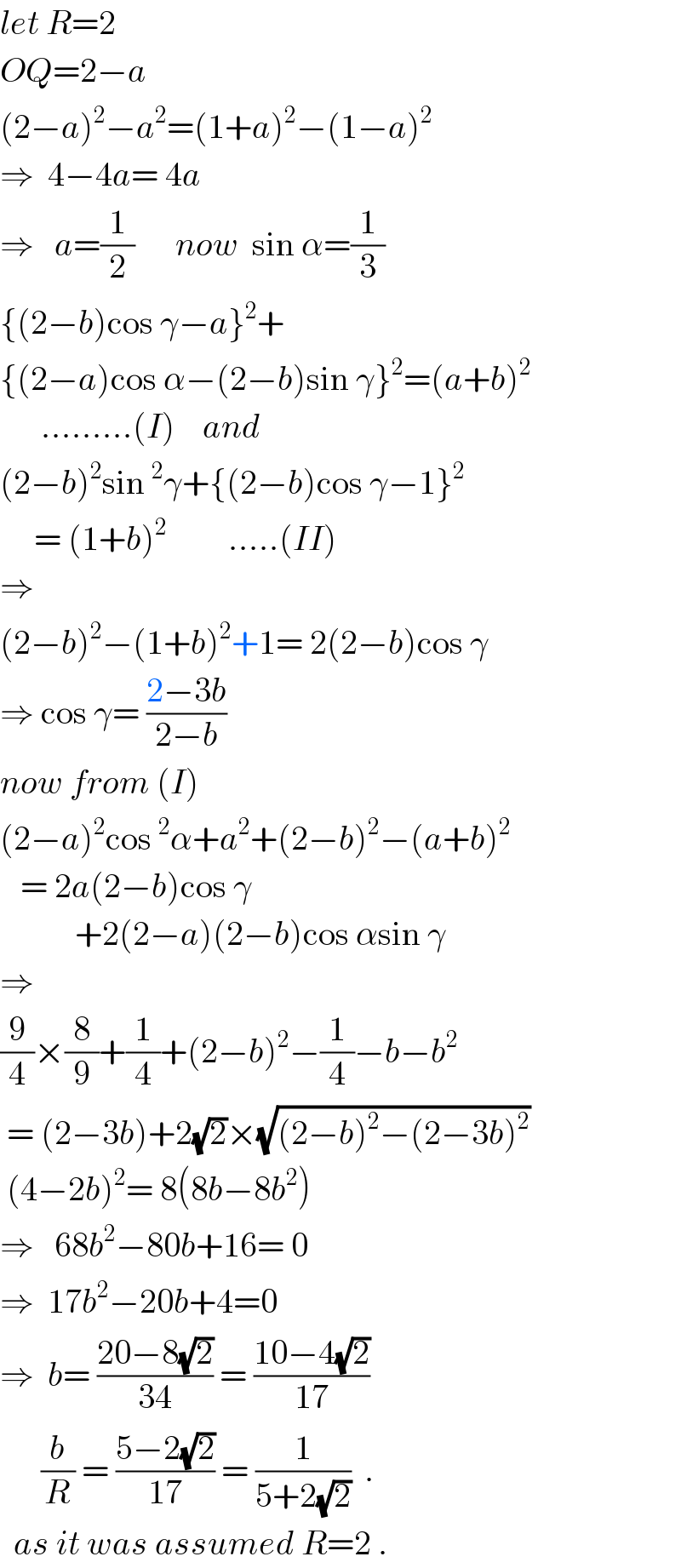
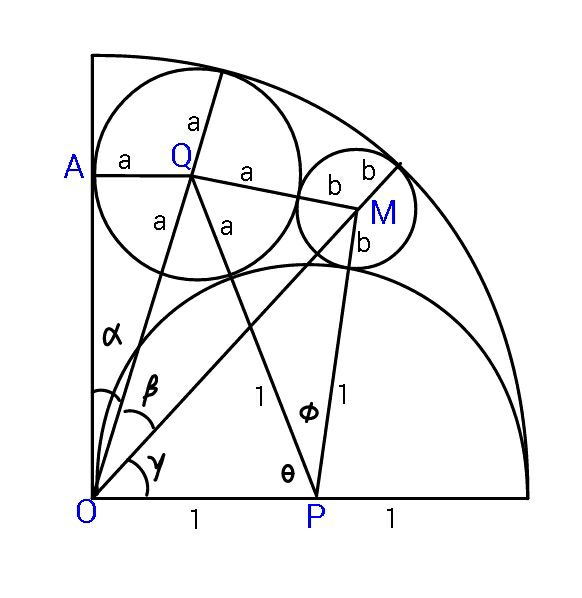
$${let}\:{R}=\mathrm{2} \\ $$$${OQ}=\mathrm{2}−{a}\: \\ $$$$\left(\mathrm{2}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} =\left(\mathrm{1}+{a}\right)^{\mathrm{2}} −\left(\mathrm{1}−{a}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{4}−\mathrm{4}{a}=\:\mathrm{4}{a}\:\:\: \\ $$$$\Rightarrow\:\:\:{a}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:{now}\:\:\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left\{\left(\mathrm{2}−{b}\right)\mathrm{cos}\:\gamma−{a}\right\}^{\mathrm{2}} + \\ $$$$\left\{\left(\mathrm{2}−{a}\right)\mathrm{cos}\:\alpha−\left(\mathrm{2}−{b}\right)\mathrm{sin}\:\gamma\right\}^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:………\left({I}\right)\:\:\:\:{and} \\ $$$$\left(\mathrm{2}−{b}\right)^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \gamma+\left\{\left(\mathrm{2}−{b}\right)\mathrm{cos}\:\gamma−\mathrm{1}\right\}^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\:\left(\mathrm{1}+{b}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:…..\left({II}\right) \\ $$$$\Rightarrow\:\: \\ $$$$\left(\mathrm{2}−{b}\right)^{\mathrm{2}} −\left(\mathrm{1}+{b}\right)^{\mathrm{2}} +\mathrm{1}=\:\mathrm{2}\left(\mathrm{2}−{b}\right)\mathrm{cos}\:\gamma \\ $$$$\Rightarrow\:\mathrm{cos}\:\gamma=\:\frac{\mathrm{2}−\mathrm{3}{b}}{\mathrm{2}−{b}} \\ $$$${now}\:{from}\:\left({I}\right) \\ $$$$\left(\mathrm{2}−{a}\right)^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \alpha+{a}^{\mathrm{2}} +\left(\mathrm{2}−{b}\right)^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} \\ $$$$\:\:\:=\:\mathrm{2}{a}\left(\mathrm{2}−{b}\right)\mathrm{cos}\:\gamma \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\left(\mathrm{2}−{a}\right)\left(\mathrm{2}−{b}\right)\mathrm{cos}\:\alpha\mathrm{sin}\:\gamma \\ $$$$\Rightarrow \\ $$$$\frac{\mathrm{9}}{\mathrm{4}}×\frac{\mathrm{8}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{4}}+\left(\mathrm{2}−{b}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}−{b}−{b}^{\mathrm{2}} \\ $$$$\:=\:\left(\mathrm{2}−\mathrm{3}{b}\right)+\mathrm{2}\sqrt{\mathrm{2}}×\sqrt{\left(\mathrm{2}−{b}\right)^{\mathrm{2}} −\left(\mathrm{2}−\mathrm{3}{b}\right)^{\mathrm{2}} } \\ $$$$\:\left(\mathrm{4}−\mathrm{2}{b}\right)^{\mathrm{2}} =\:\mathrm{8}\left(\mathrm{8}{b}−\mathrm{8}{b}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\:\mathrm{68}{b}^{\mathrm{2}} −\mathrm{80}{b}+\mathrm{16}=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{17}{b}^{\mathrm{2}} −\mathrm{20}{b}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\:\:{b}=\:\frac{\mathrm{20}−\mathrm{8}\sqrt{\mathrm{2}}}{\mathrm{34}}\:=\:\frac{\mathrm{10}−\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{17}} \\ $$$$\:\:\:\:\:\:\frac{{b}}{{R}}\:=\:\frac{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{17}}\:=\:\frac{\mathrm{1}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}}\:\:. \\ $$$$\:\:{as}\:{it}\:{was}\:{assumed}\:{R}=\mathrm{2}\:. \\ $$
Commented by mr W last updated on 25/Nov/19
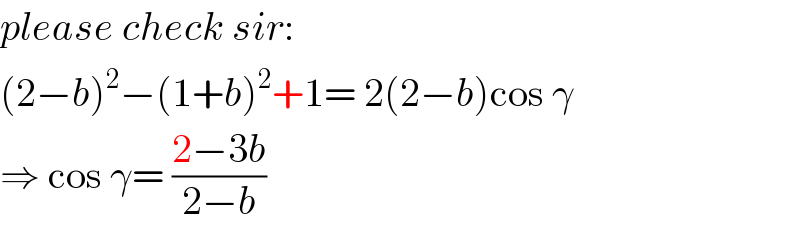
$${please}\:{check}\:{sir}: \\ $$$$\left(\mathrm{2}−{b}\right)^{\mathrm{2}} −\left(\mathrm{1}+{b}\right)^{\mathrm{2}} +\mathrm{1}=\:\mathrm{2}\left(\mathrm{2}−{b}\right)\mathrm{cos}\:\gamma \\ $$$$\Rightarrow\:\mathrm{cos}\:\gamma=\:\frac{\mathrm{2}−\mathrm{3}{b}}{\mathrm{2}−{b}} \\ $$
Commented by ajfour last updated on 25/Nov/19
$${many}\:{many}\:{thanks}\:{sir}! \\ $$
Answered by mr W last updated on 25/Nov/19
Commented by mr W last updated on 25/Nov/19
$${OB}={R}−{a} \\ $$$${OC}={R}−{b} \\ $$$${BC}={a}+{b} \\ $$$${DB}=\frac{{R}}{\mathrm{2}}+{a} \\ $$$${DC}=\frac{{R}}{\mathrm{2}}+{b} \\ $$$$\mathrm{sin}\:\alpha=\frac{{a}}{{R}−{a}} \\ $$$$\mathrm{cos}\:\beta=\frac{\left({R}−{b}\right)^{\mathrm{2}} +\frac{{R}^{\mathrm{2}} }{\mathrm{4}}−\left(\frac{{R}}{\mathrm{2}}+{b}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}−{b}\right)\frac{{R}}{\mathrm{2}}}=\frac{{R}−\mathrm{3}{b}}{{R}−{b}} \\ $$$$\mathrm{cos}\:\gamma=\frac{\left({R}−{a}\right)^{\mathrm{2}} +\left({R}−{b}\right)^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}−{a}\right)\left({R}−{b}\right)} \\ $$$$=\frac{{R}^{\mathrm{2}} −{R}\left({a}+{b}\right)−{ab}}{\left({R}−{a}\right)\left({R}−{b}\right)} \\ $$$$\mathrm{cos}\:\left(\beta+\gamma\right)=\frac{\left({R}−{a}\right)^{\mathrm{2}} +\frac{{R}^{\mathrm{2}} }{\mathrm{4}}−\left(\frac{{R}}{\mathrm{2}}+{a}\right)^{\mathrm{2}} }{\mathrm{2}\left({R}−{a}\right)\frac{{R}}{\mathrm{2}}}=\frac{{R}−\mathrm{3}{a}}{{R}−{a}} \\ $$$$\mathrm{cos}\:\left(\beta+\gamma\right)=\mathrm{sin}\:\alpha \\ $$$$\frac{{R}−\mathrm{3}{a}}{{R}−{a}}=\frac{{a}}{{R}−{a}} \\ $$$${R}^{\mathrm{2}} −\mathrm{5}{Ra}+\mathrm{4}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({R}−\mathrm{4}{a}\right)\left({R}−{a}\right)=\mathrm{0} \\ $$$$\Rightarrow{R}=\mathrm{4}{a}\:\Rightarrow{a}=\frac{{R}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\left(\beta+\gamma\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\gamma=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}−\beta \\ $$$$\mathrm{cos}\:\gamma=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}\:\beta+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{sin}\:\beta \\ $$$$\mathrm{cos}\:\gamma=\frac{\mathrm{3}{R}−\mathrm{5}{b}}{\mathrm{3}\left({R}−{b}\right)} \\ $$$$\mathrm{cos}\:\beta=\frac{{R}−\mathrm{3}{b}}{{R}−{b}}\:\Rightarrow\mathrm{sin}\:\beta=\frac{\mathrm{2}\sqrt{\left({R}−\mathrm{2}{b}\right){b}}}{{R}−{b}} \\ $$$$\frac{\mathrm{3}{R}−\mathrm{5}{b}}{\mathrm{2}\left({R}−{b}\right)}=\frac{{R}−\mathrm{3}{b}}{\mathrm{3}\left({R}−{b}\right)}+\frac{\mathrm{4}\sqrt{\mathrm{2}\left({R}−\mathrm{2}{b}\right){b}}}{\mathrm{3}\left({R}−{b}\right)} \\ $$$${R}−{b}=\mathrm{2}\sqrt{\mathrm{2}{b}\left({R}−\mathrm{2}{b}\right)} \\ $$$${R}^{\mathrm{2}} −\mathrm{2}{Rb}+{b}^{\mathrm{2}} =\mathrm{8}{b}\left({R}−\mathrm{2}{b}\right) \\ $$$${R}^{\mathrm{2}} −\mathrm{10}{Rb}+\mathrm{17}{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{b}=\frac{{R}}{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}}\approx\mathrm{0}.\mathrm{12774}{R} \\ $$
Commented by Maclaurin Stickker last updated on 25/Nov/19
$${Another}\:{perfect}\:{answer}.\:{Thank}\:{you}. \\ $$
