Question Number 7453 by ankit036 last updated on 30/Aug/16

Commented by Rasheed Soomro last updated on 30/Aug/16

$$\left(\mathrm{A}\right)\:\:\mathrm{1} \\ $$
Answered by afy1991 last updated on 30/Aug/16

$${c}\:{option}\:{is}\:{ri}\mathrm{8}. \\ $$
Commented by FilupSmith last updated on 30/Aug/16
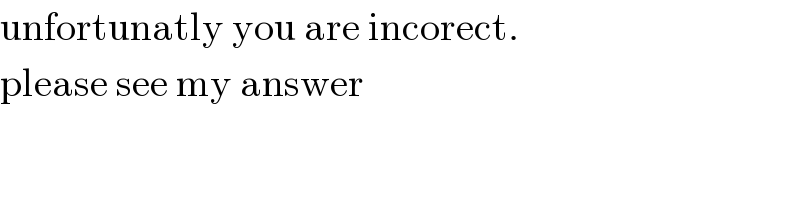
$$\mathrm{unfortunatly}\:\mathrm{you}\:\mathrm{are}\:\mathrm{incorect}. \\ $$$$\mathrm{please}\:\mathrm{see}\:\mathrm{my}\:\mathrm{answer} \\ $$
Answered by FilupSmith last updated on 30/Aug/16
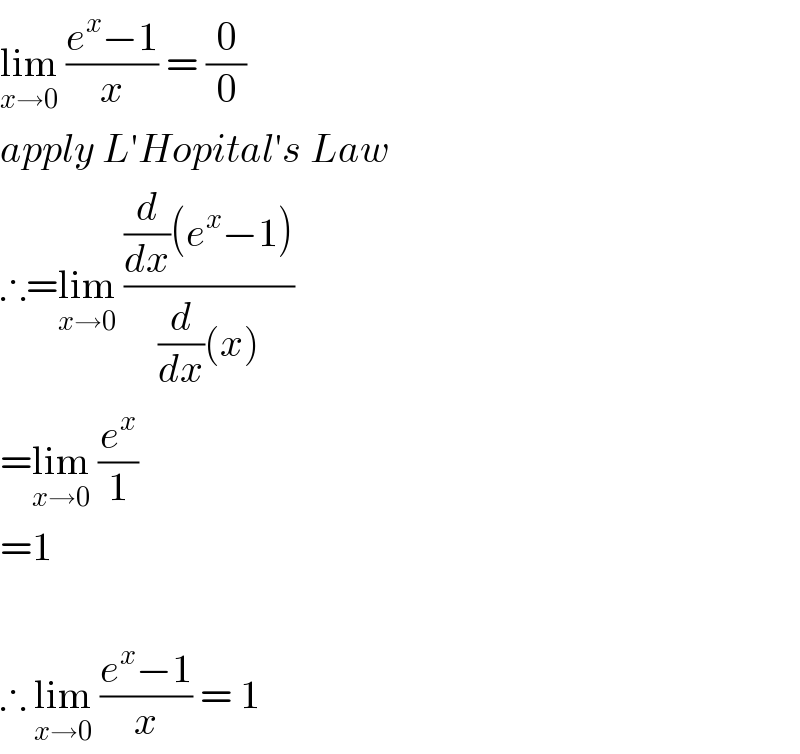
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} −\mathrm{1}}{{x}}\:=\:\frac{\mathrm{0}}{\mathrm{0}} \\ $$$${apply}\:{L}'{Hopital}'{s}\:{Law} \\ $$$$\therefore=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\left({e}^{{x}} −\mathrm{1}\right)}{\frac{{d}}{{dx}}\left({x}\right)} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} }{\mathrm{1}} \\ $$$$=\mathrm{1} \\ $$$$ \\ $$$$\therefore\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} −\mathrm{1}}{{x}}\:=\:\mathrm{1} \\ $$
