Question Number 74580 by chess1 last updated on 26/Nov/19
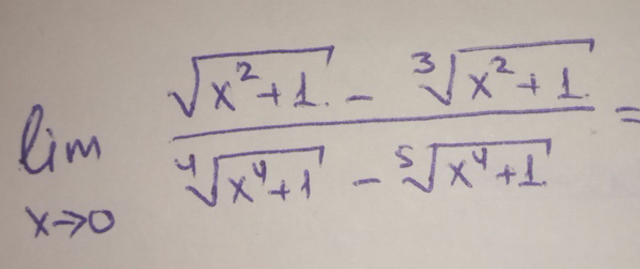
Answered by mind is power last updated on 26/Nov/19
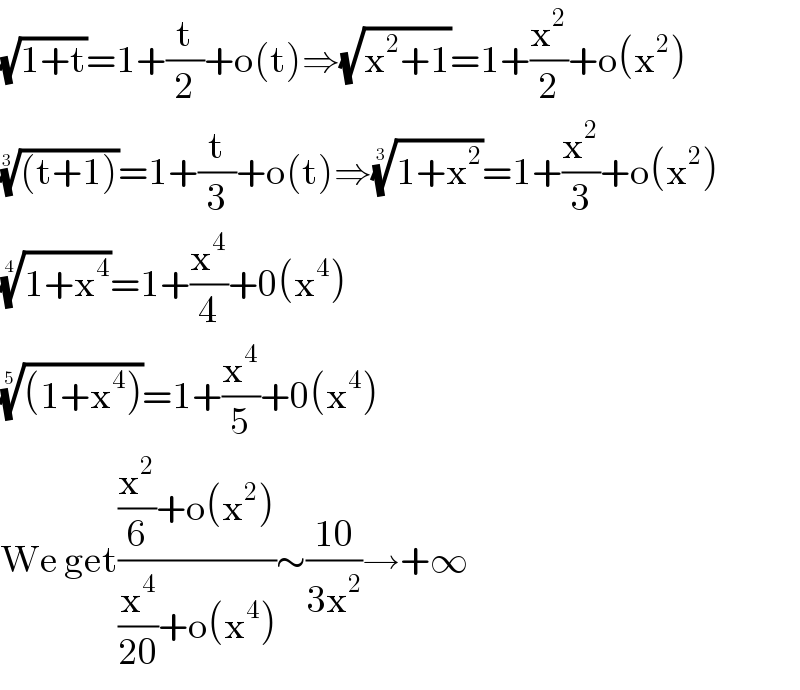
$$\sqrt{\mathrm{1}+\mathrm{t}}=\mathrm{1}+\frac{\mathrm{t}}{\mathrm{2}}+\mathrm{o}\left(\mathrm{t}\right)\Rightarrow\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}=\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\sqrt[{\mathrm{3}}]{\left(\mathrm{t}+\mathrm{1}\right)}=\mathrm{1}+\frac{\mathrm{t}}{\mathrm{3}}+\mathrm{o}\left(\mathrm{t}\right)\Rightarrow\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }=\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{3}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\sqrt[{\mathrm{4}}]{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }=\mathrm{1}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}}+\mathrm{0}\left(\mathrm{x}^{\mathrm{4}} \right) \\ $$$$\sqrt[{\mathrm{5}}]{\left(\mathrm{1}+\mathrm{x}^{\mathrm{4}} \right)}=\mathrm{1}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{5}}+\mathrm{0}\left(\mathrm{x}^{\mathrm{4}} \right) \\ $$$$\mathrm{We}\:\mathrm{get}\frac{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)}{\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{20}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right)}\sim\frac{\mathrm{10}}{\mathrm{3x}^{\mathrm{2}} }\rightarrow+\infty \\ $$
Commented by chess1 last updated on 27/Nov/19

$$\mathrm{thanks} \\ $$
