Menu Close

Question-74594

Tinku Tara 0 Comments
Pin




Question Number 74594 by ajfour last updated on 27/Nov/19
Commented by ajfour last updated on 27/Nov/19
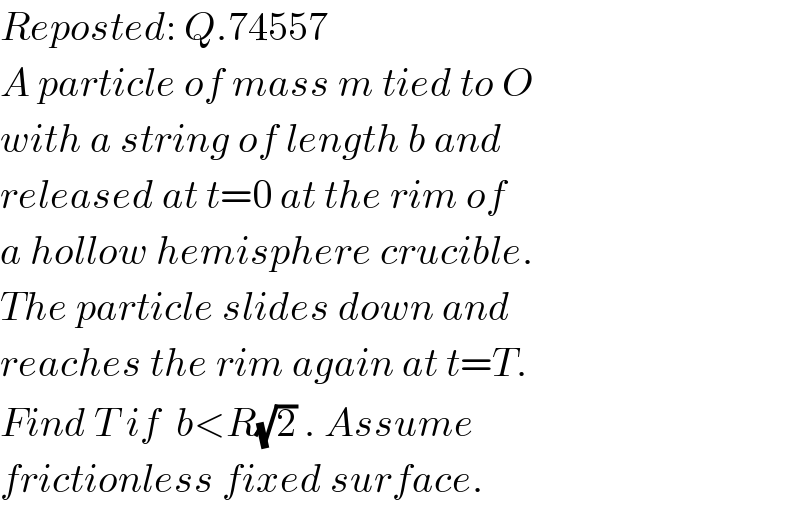
Reposted: Q.74557 A particle of mass m tied to O with a string of length b and released at t=0 at the rim of a hollow hemisphere crucible. The particle slides down and reaches the rim again at t=T. Find T if b<R(√2) . Assume frictionless fixed surface.
$${Reposted}:\:{Q}.\mathrm{74557} \\ $$$${A}\:{particle}\:{of}\:{mass}\:{m}\:{tied}\:{to}\:{O} \\ $$$${with}\:{a}\:{string}\:{of}\:{length}\:{b}\:{and} \\ $$$${released}\:{at}\:{t}=\mathrm{0}\:{at}\:{the}\:{rim}\:{of} \\ $$$${a}\:{hollow}\:{hemisphere}\:{crucible}. \\ $$$${The}\:{particle}\:{slides}\:{down}\:{and} \\ $$$${reaches}\:{the}\:{rim}\:{again}\:{at}\:{t}={T}. \\ $$$${Find}\:{T}\:{if}\:\:{b}<{R}\sqrt{\mathrm{2}}\:.\:{Assume} \\ $$$${frictionless}\:{fixed}\:{surface}. \\ $$
Answered by ajfour last updated on 27/Nov/19
Commented by ajfour last updated on 27/Nov/19
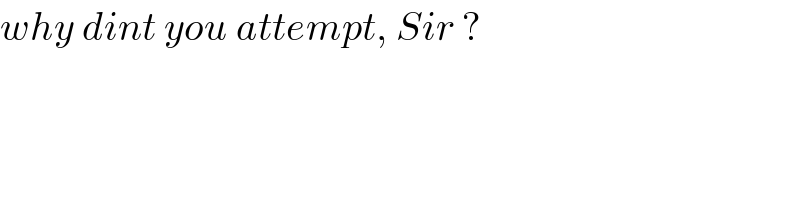
why dint you attempt, Sir ?
$${why}\:{dint}\:{you}\:{attempt},\:{Sir}\:? \\ $$
Commented by mr W last updated on 27/Nov/19
i saw your attemp in the early post. i thought there is maybe an other way to solve: we find at first the orbit of the mass in terms of a parameter θ, and then the velocity also in terms of θ acc. to ((mv^2 )/2)=mgΔh(θ). but i had no time to work it out. then i saw this solution of yours. that is similar to that what i thought of. i didn′t expect that we can get such a simple result.
$${i}\:{saw}\:{your}\:{attemp}\:{in}\:{the}\:{early}\:{post}.\: \\ $$$${i}\:{thought}\:{there}\:{is}\:{maybe}\:{an}\:{other}\:{way} \\ $$$${to}\:{solve}:\:{we}\:{find}\:{at}\:{first}\:{the}\:{orbit}\:{of} \\ $$$${the}\:{mass}\:{in}\:{terms}\:{of}\:{a}\:{parameter}\:\theta, \\ $$$${and}\:{then}\:{the}\:{velocity}\:{also}\:{in}\:{terms}\:{of} \\ $$$$\theta\:{acc}.\:{to}\:\frac{{mv}^{\mathrm{2}} }{\mathrm{2}}={mg}\Delta{h}\left(\theta\right).\:{but}\:{i}\:{had}\:{no} \\ $$$${time}\:{to}\:{work}\:{it}\:{out}.\:{then}\:{i}\:{saw}\:{this} \\ $$$${solution}\:{of}\:{yours}.\:{that}\:{is}\:{similar}\:{to} \\ $$$${that}\:{what}\:{i}\:{thought}\:{of}.\:{i}\:{didn}'{t} \\ $$$${expect}\:{that}\:{we}\:{can}\:{get}\:{such}\:{a}\:{simple} \\ $$$${result}. \\ $$
Commented by mr W last updated on 27/Nov/19
nice solution!
$${nice}\:{solution}! \\ $$
Commented by ajfour last updated on 27/Nov/19
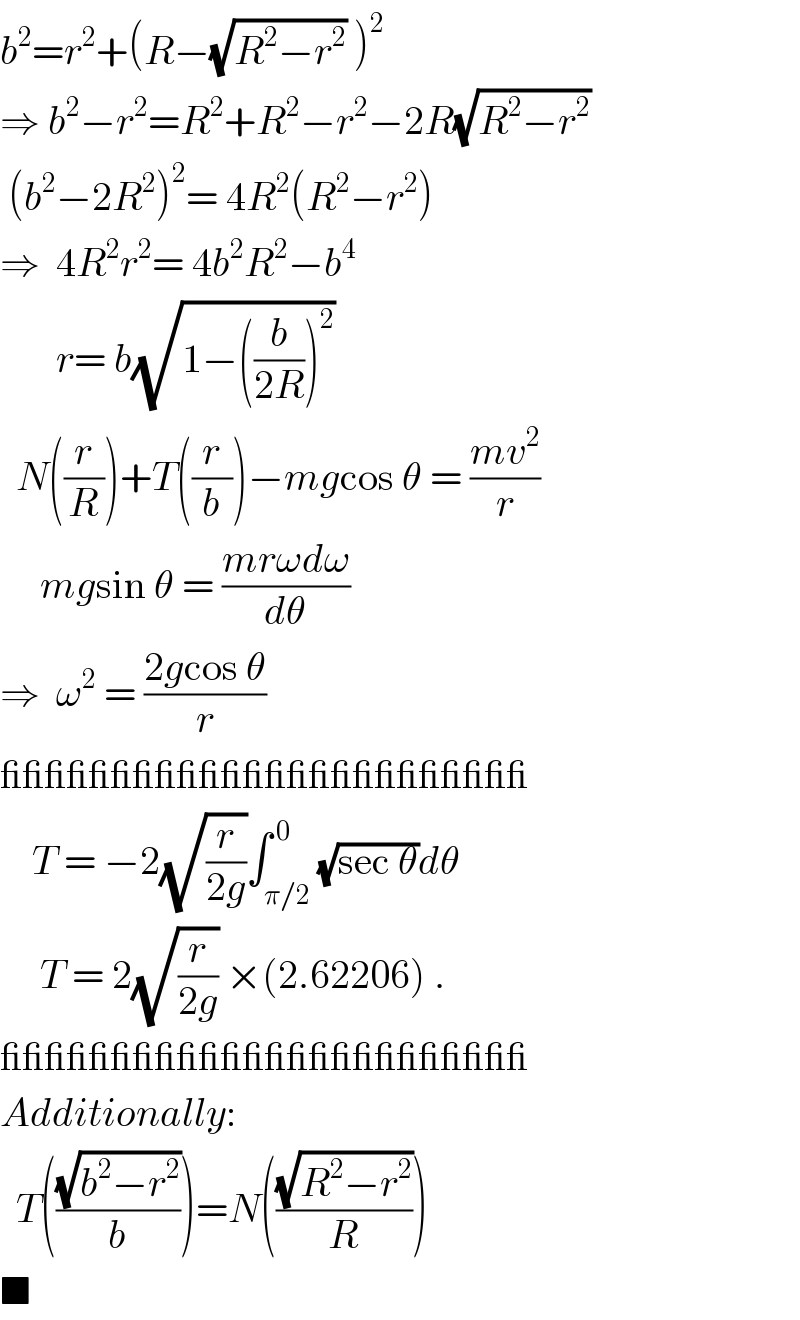
b^2 =r^2 +(R−(√(R^2 −r^2 )) )^2 ⇒ b^2 −r^2 =R^2 +R^2 −r^2 −2R(√(R^2 −r^2 )) (b^2 −2R^2 )^2 = 4R^2 (R^2 −r^2 ) ⇒ 4R^2 r^2 = 4b^2 R^2 −b^4 r= b(√(1−((b/(2R)))^2 )) N((r/R))+T((r/b))−mgcos θ = ((mv^2 )/r) mgsin θ = ((mrωdω)/dθ) ⇒ ω^2 = ((2gcos θ)/r) ________________________ T = −2(√(r/(2g)))∫_(π/2) ^( 0) (√(sec θ))dθ T = 2(√(r/(2g))) ×(2.62206) . ________________________ Additionally: T(((√(b^2 −r^2 ))/b))=N(((√(R^2 −r^2 ))/R)) ■
$${b}^{\mathrm{2}} ={r}^{\mathrm{2}} +\left({R}−\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }\:\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} −{r}^{\mathrm{2}} ={R}^{\mathrm{2}} +{R}^{\mathrm{2}} −{r}^{\mathrm{2}} −\mathrm{2}{R}\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$$\:\left({b}^{\mathrm{2}} −\mathrm{2}{R}^{\mathrm{2}} \right)^{\mathrm{2}} =\:\mathrm{4}{R}^{\mathrm{2}} \left({R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\mathrm{4}{R}^{\mathrm{2}} {r}^{\mathrm{2}} =\:\mathrm{4}{b}^{\mathrm{2}} {R}^{\mathrm{2}} −{b}^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:{r}=\:{b}\sqrt{\mathrm{1}−\left(\frac{{b}}{\mathrm{2}{R}}\right)^{\mathrm{2}} } \\ $$$$\:\:{N}\left(\frac{{r}}{{R}}\right)+{T}\left(\frac{{r}}{{b}}\right)−{mg}\mathrm{cos}\:\theta\:=\:\frac{{mv}^{\mathrm{2}} }{{r}} \\ $$$$\:\:\:\:\:{mg}\mathrm{sin}\:\theta\:=\:\frac{{mr}\omega{d}\omega}{{d}\theta} \\ $$$$\Rightarrow\:\:\omega^{\mathrm{2}} \:=\:\frac{\mathrm{2}{g}\mathrm{cos}\:\theta}{{r}} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\:{T}\:=\:−\mathrm{2}\sqrt{\frac{{r}}{\mathrm{2}{g}}}\int_{\pi/\mathrm{2}} ^{\:\mathrm{0}} \sqrt{\mathrm{sec}\:\theta}{d}\theta\: \\ $$$$\:\:\:\:\:{T}\:=\:\mathrm{2}\sqrt{\frac{{r}}{\mathrm{2}{g}}}\:×\left(\mathrm{2}.\mathrm{62206}\right)\:. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${Additionally}: \\ $$$$\:\:{T}\left(\frac{\sqrt{{b}^{\mathrm{2}} −{r}^{\mathrm{2}} }}{{b}}\right)={N}\left(\frac{\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }}{{R}}\right) \\ $$$$\blacksquare \\ $$
Commented by ajfour last updated on 27/Nov/19
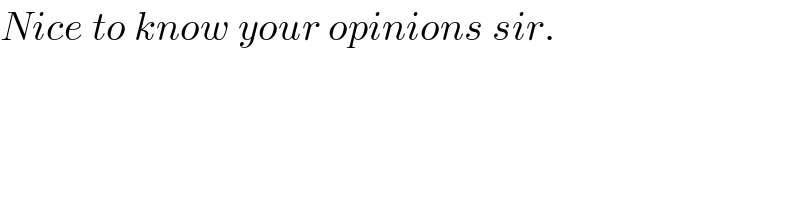
Nice to know your opinions sir.
$${Nice}\:{to}\:{know}\:{your}\:{opinions}\:{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *