Question Number 74611 by chess1 last updated on 27/Nov/19
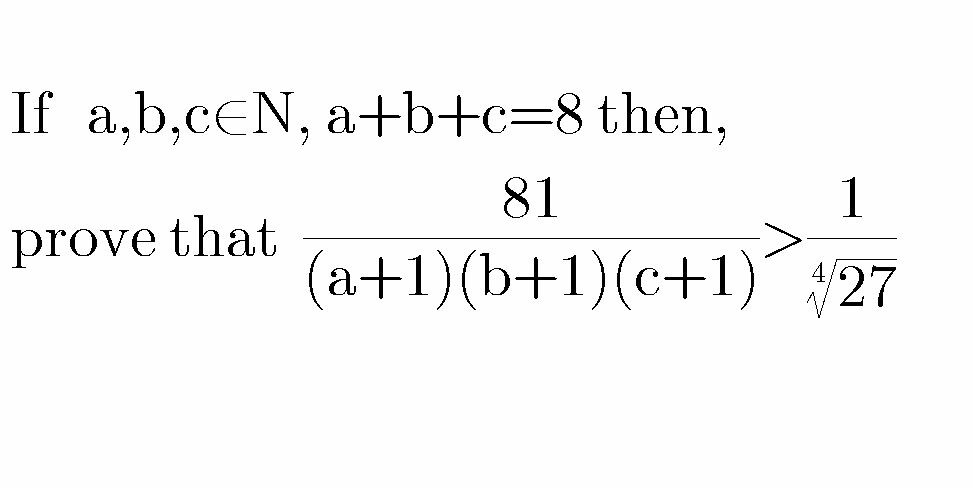
Answered by mind is power last updated on 27/Nov/19
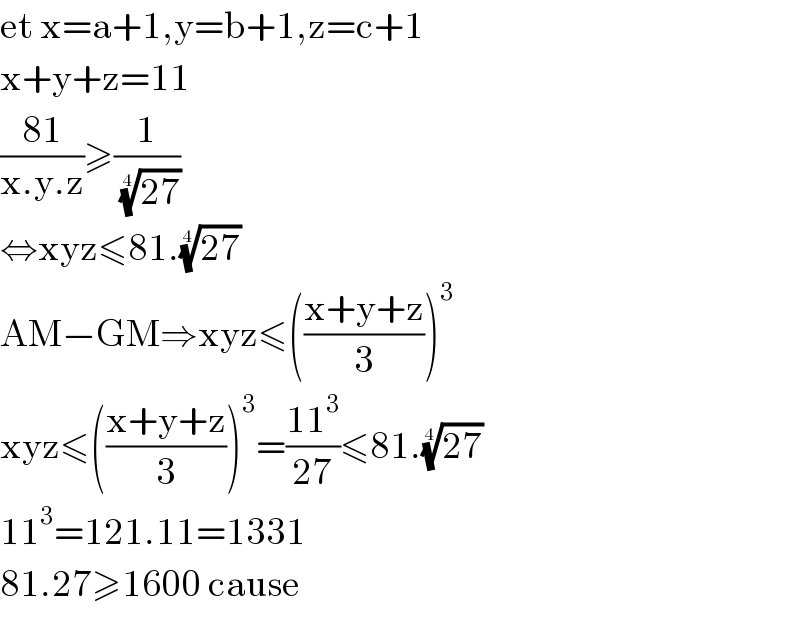
$$\mathrm{et}\:\mathrm{x}=\mathrm{a}+\mathrm{1},\mathrm{y}=\mathrm{b}+\mathrm{1},\mathrm{z}=\mathrm{c}+\mathrm{1} \\ $$$$\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{11} \\ $$$$\frac{\mathrm{81}}{\mathrm{x}.\mathrm{y}.\mathrm{z}}\geqslant\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{27}}} \\ $$$$\Leftrightarrow\mathrm{xyz}\leqslant\mathrm{81}.\sqrt[{\mathrm{4}}]{\mathrm{27}} \\ $$$$\mathrm{AM}−\mathrm{GM}\Rightarrow\mathrm{xyz}\leqslant\left(\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$\mathrm{xyz}\leqslant\left(\frac{\mathrm{x}+\mathrm{y}+\mathrm{z}}{\mathrm{3}}\right)^{\mathrm{3}} =\frac{\mathrm{11}^{\mathrm{3}} }{\mathrm{27}}\leqslant\mathrm{81}.\sqrt[{\mathrm{4}}]{\mathrm{27}}\:\:\:\: \\ $$$$\mathrm{11}^{\mathrm{3}} =\mathrm{121}.\mathrm{11}=\mathrm{1331} \\ $$$$\mathrm{81}.\mathrm{27}\geqslant\mathrm{1600}\:\mathrm{cause} \\ $$
Commented by chess1 last updated on 27/Nov/19

$$\mathrm{thanks} \\ $$
Commented by mind is power last updated on 27/Nov/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$
