Question Number 74621 by aliesam last updated on 27/Nov/19

Commented by mathmax by abdo last updated on 28/Nov/19
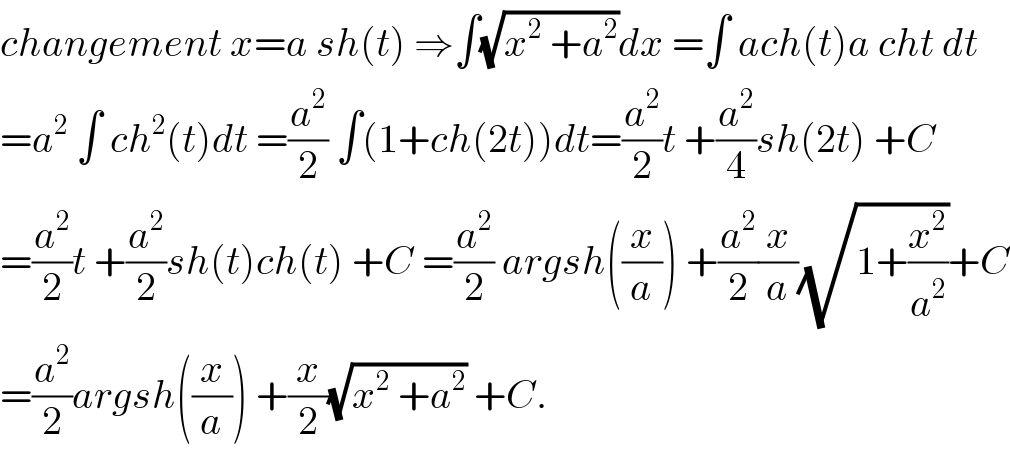
$${changement}\:{x}={a}\:{sh}\left({t}\right)\:\Rightarrow\int\sqrt{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx}\:=\int\:{ach}\left({t}\right){a}\:{cht}\:{dt} \\ $$$$={a}^{\mathrm{2}} \:\int\:{ch}^{\mathrm{2}} \left({t}\right){dt}\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\:\int\left(\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)\right){dt}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{t}\:+\frac{{a}^{\mathrm{2}} }{\mathrm{4}}{sh}\left(\mathrm{2}{t}\right)\:+{C} \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{t}\:+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sh}\left({t}\right){ch}\left({t}\right)\:+{C}\:=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\:{argsh}\left(\frac{{x}}{{a}}\right)\:+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\frac{{x}}{{a}}\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }}+{C} \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{argsh}\left(\frac{{x}}{{a}}\right)\:+\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\:+{C}. \\ $$
Answered by MJS last updated on 28/Nov/19
![∫f(x)=F(x) ⇔ (dF/dx)=f(x) (d/dx)[(x/2)(√(x^2 +q^2 ))+(q^2 /2)sinh^(−1) (x/q)]= =((2x^2 +q^2 )/(2(√(x^2 +q^2 ))))+(q^2 /(2(√(x^2 +q^2 ))))=((x^2 +q^2 )/( (√(x^2 +q^2 ))))=(√(x^2 +q^2 ))](https://www.tinkutara.com/question/Q74646.png)
$$\int{f}\left({x}\right)={F}\left({x}\right)\:\Leftrightarrow\:\frac{{dF}}{{dx}}={f}\left({x}\right) \\ $$$$\frac{{d}}{{dx}}\left[\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} +{q}^{\mathrm{2}} }+\frac{{q}^{\mathrm{2}} }{\mathrm{2}}\mathrm{sinh}^{−\mathrm{1}} \:\frac{{x}}{{q}}\right]= \\ $$$$=\frac{\mathrm{2}{x}^{\mathrm{2}} +{q}^{\mathrm{2}} }{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{q}^{\mathrm{2}} }}+\frac{{q}^{\mathrm{2}} }{\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{q}^{\mathrm{2}} }}=\frac{{x}^{\mathrm{2}} +{q}^{\mathrm{2}} }{\:\sqrt{{x}^{\mathrm{2}} +{q}^{\mathrm{2}} }}=\sqrt{{x}^{\mathrm{2}} +{q}^{\mathrm{2}} } \\ $$
