Question Number 74649 by ajfour last updated on 28/Nov/19

Commented by ajfour last updated on 28/Nov/19
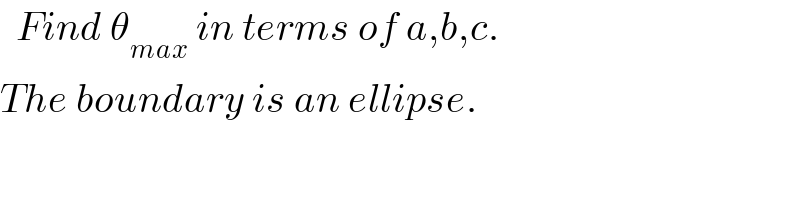
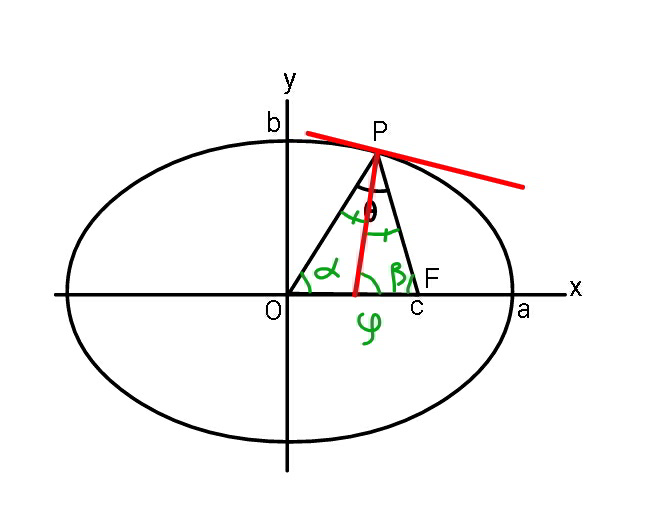
$$\:\:{Find}\:\theta_{{max}} \:{in}\:{terms}\:{of}\:{a},{b},{c}. \\ $$$${The}\:{boundary}\:{is}\:{an}\:{ellipse}. \\ $$
Answered by ajfour last updated on 28/Nov/19
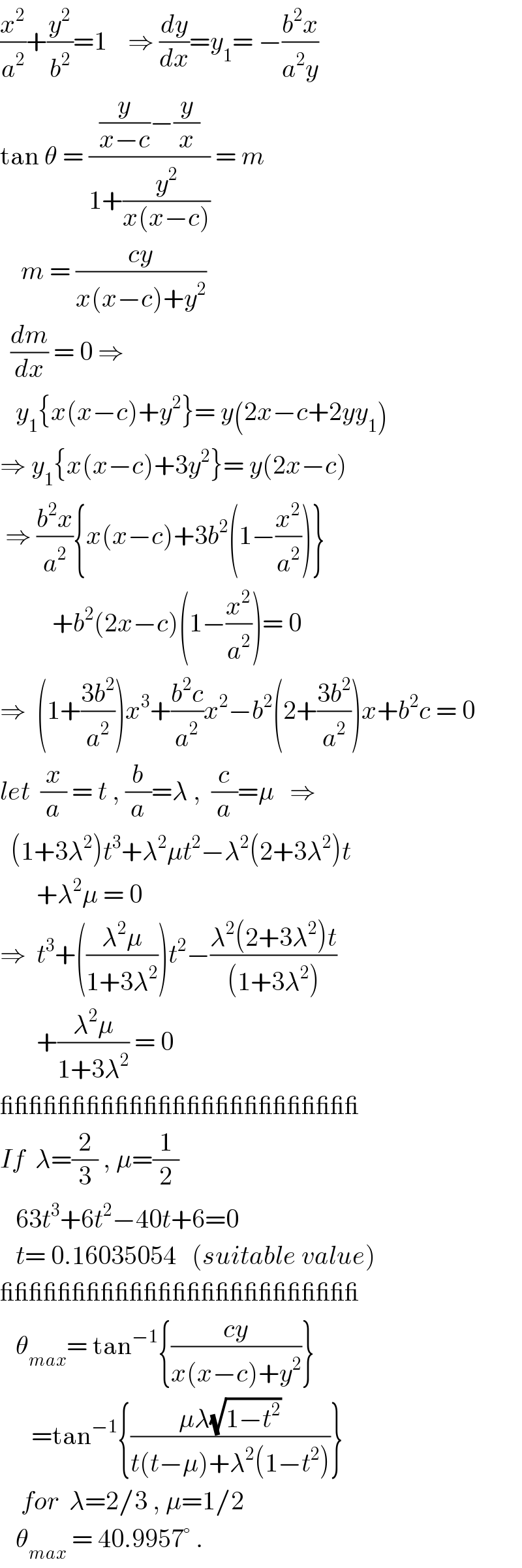
$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1}\:\:\:\:\Rightarrow\:\frac{{dy}}{{dx}}={y}_{\mathrm{1}} =\:−\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} {y}} \\ $$$$\mathrm{tan}\:\theta\:=\:\frac{\frac{{y}}{{x}−{c}}−\frac{{y}}{{x}}}{\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}\left({x}−{c}\right)}}\:=\:{m} \\ $$$$\:\:\:\:{m}\:=\:\frac{{cy}}{{x}\left({x}−{c}\right)+{y}^{\mathrm{2}} } \\ $$$$\:\:\frac{{dm}}{{dx}}\:=\:\mathrm{0}\:\Rightarrow\: \\ $$$$\:\:\:{y}_{\mathrm{1}} \left\{{x}\left({x}−{c}\right)+{y}^{\mathrm{2}} \right\}=\:{y}\left(\mathrm{2}{x}−{c}+\mathrm{2}{yy}_{\mathrm{1}} \right) \\ $$$$\Rightarrow\:{y}_{\mathrm{1}} \left\{{x}\left({x}−{c}\right)+\mathrm{3}{y}^{\mathrm{2}} \right\}=\:{y}\left(\mathrm{2}{x}−{c}\right) \\ $$$$\:\Rightarrow\:\frac{{b}^{\mathrm{2}} {x}}{{a}^{\mathrm{2}} }\left\{{x}\left({x}−{c}\right)+\mathrm{3}{b}^{\mathrm{2}} \left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:+{b}^{\mathrm{2}} \left(\mathrm{2}{x}−{c}\right)\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right)=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mathrm{1}+\frac{\mathrm{3}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right){x}^{\mathrm{3}} +\frac{{b}^{\mathrm{2}} {c}}{{a}^{\mathrm{2}} }{x}^{\mathrm{2}} −{b}^{\mathrm{2}} \left(\mathrm{2}+\frac{\mathrm{3}{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\right){x}+{b}^{\mathrm{2}} {c}\:=\:\mathrm{0} \\ $$$${let}\:\:\frac{{x}}{{a}}\:=\:{t}\:,\:\frac{{b}}{{a}}=\lambda\:,\:\:\frac{{c}}{{a}}=\mu\:\:\:\Rightarrow \\ $$$$\:\:\left(\mathrm{1}+\mathrm{3}\lambda^{\mathrm{2}} \right){t}^{\mathrm{3}} +\lambda^{\mathrm{2}} \mu{t}^{\mathrm{2}} −\lambda^{\mathrm{2}} \left(\mathrm{2}+\mathrm{3}\lambda^{\mathrm{2}} \right){t} \\ $$$$\:\:\:\:\:\:\:+\lambda^{\mathrm{2}} \mu\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{3}} +\left(\frac{\lambda^{\mathrm{2}} \mu}{\mathrm{1}+\mathrm{3}\lambda^{\mathrm{2}} }\right){t}^{\mathrm{2}} −\frac{\lambda^{\mathrm{2}} \left(\mathrm{2}+\mathrm{3}\lambda^{\mathrm{2}} \right){t}}{\left(\mathrm{1}+\mathrm{3}\lambda^{\mathrm{2}} \right)} \\ $$$$\:\:\:\:\:\:\:+\frac{\lambda^{\mathrm{2}} \mu}{\mathrm{1}+\mathrm{3}\lambda^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${If}\:\:\lambda=\frac{\mathrm{2}}{\mathrm{3}}\:,\:\mu=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\mathrm{63}{t}^{\mathrm{3}} +\mathrm{6}{t}^{\mathrm{2}} −\mathrm{40}{t}+\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:{t}=\:\mathrm{0}.\mathrm{16035054}\:\:\:\left({suitable}\:{value}\right) \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\:\:\:\theta_{{max}} =\:\mathrm{tan}^{−\mathrm{1}} \left\{\frac{{cy}}{{x}\left({x}−{c}\right)+{y}^{\mathrm{2}} }\right\} \\ $$$$\:\:\:\:\:\:=\mathrm{tan}^{−\mathrm{1}} \left\{\frac{\mu\lambda\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{{t}\left({t}−\mu\right)+\lambda^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)}\right\} \\ $$$$\:\:\:\:{for}\:\:\lambda=\mathrm{2}/\mathrm{3}\:,\:\mu=\mathrm{1}/\mathrm{2} \\ $$$$\:\:\:\theta_{{max}} \:=\:\mathrm{40}.\mathrm{9957}°\:. \\ $$
Commented by ajfour last updated on 29/Nov/19
$${Sir},\:{do}\:{you}\:{agree}\:{with}\:{this}\:{answer}? \\ $$
Commented by mr W last updated on 29/Nov/19
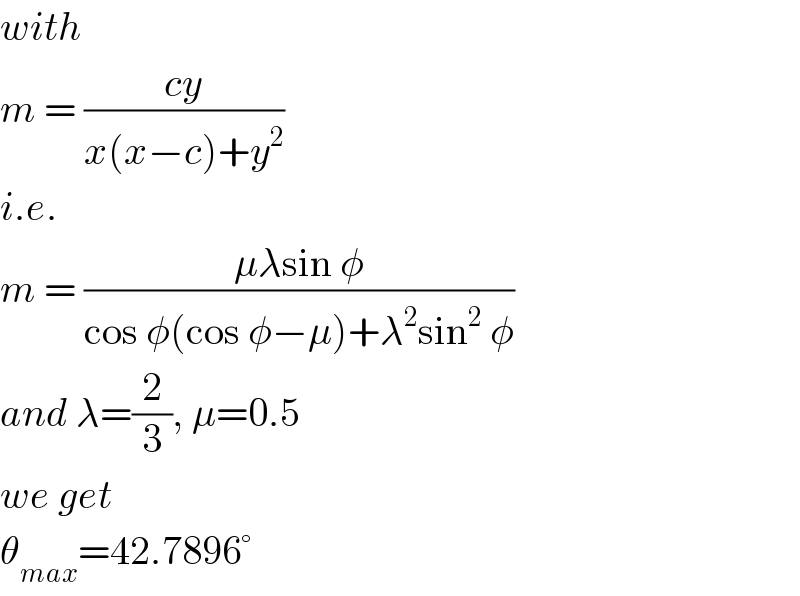
$${with} \\ $$$${m}\:=\:\frac{{cy}}{{x}\left({x}−{c}\right)+{y}^{\mathrm{2}} } \\ $$$${i}.{e}. \\ $$$${m}\:=\:\frac{\mu\lambda\mathrm{sin}\:\phi}{\mathrm{cos}\:\phi\left(\mathrm{cos}\:\phi−\mu\right)+\lambda^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\phi} \\ $$$${and}\:\lambda=\frac{\mathrm{2}}{\mathrm{3}},\:\mu=\mathrm{0}.\mathrm{5} \\ $$$${we}\:{get} \\ $$$$\theta_{{max}} =\mathrm{42}.\mathrm{7896}° \\ $$
Answered by mr W last updated on 28/Nov/19
Commented by mr W last updated on 28/Nov/19
Commented by mr W last updated on 28/Nov/19
![let λ=(b/a), μ=(c/a) P(a cos φ, b sin φ) tan α=(b/a)tan φ=λ tan φ tan ϕ=(a/b)tan φ=((tan φ)/λ) tan β=((b sin φ)/(c−a cos φ))=((λ sin φ)/(μ−cos φ)) α=ϕ−(θ/2) ⇒θ=2ϕ−2α β=π−α−θ ⇒β=π−2ϕ+α ⇒2ϕ=π−(β−α) ⇒tan 2ϕ=tan (α−β) ⇒(((2 tan φ)/λ)/(1−((tan^2 φ)/λ^2 )))=((λ tan φ−((λ sin φ)/(μ−cos φ)))/(1+λ tan φ×((λ sin φ)/(μ−cos φ)))) ⇒((2 tan φ)/(λ^2 −tan^2 φ))=((tan φ(μ−cos φ)−sin φ)/(μ−cos φ+λ^2 sin φ tan φ)) ⇒((2 cos φ)/((1+λ^2 )cos^2 φ−1))=((μ−2 cos φ)/(λ^2 +μ cos φ−(1+λ^2 )cos^2 φ)) let t=cos φ ⇒((2t)/((1+λ^2 )t^2 −1))=((μ−2t)/(λ^2 +μt−(1+λ^2 )t^2 )) ⇒t^2 −(2/μ)t+(1/(1−λ^2 ))=0 ⇒t=(1/μ)−(√((1/μ^2 )−(1/(1−λ^2 )))) ⇒φ=cos^(−1) ((1/μ)−(√((1/μ^2 )−(1/(1−λ^2 ))))) ⇒θ_(max) =2[tan^(−1) (((tan φ)/λ))−tan^(−1) (λ tan φ)] example: λ=(b/a)=(2/3), μ=(c/a)=(1/2) ⇒t=2−(√((11)/5)) ⇒φ=cos^(−1) (2−(√((11)/5)))=58.8845° ⇒α=47.8429° ⇒ϕ=68.0799° ⇒β=91.6831° ⇒θ_(max) =2(68.0799−47.8429)=40.474°](https://www.tinkutara.com/question/Q74670.png)
$${let}\:\lambda=\frac{{b}}{{a}},\:\mu=\frac{{c}}{{a}} \\ $$$${P}\left({a}\:\mathrm{cos}\:\phi,\:{b}\:\mathrm{sin}\:\phi\right) \\ $$$$\mathrm{tan}\:\alpha=\frac{{b}}{{a}}\mathrm{tan}\:\phi=\lambda\:\mathrm{tan}\:\phi \\ $$$$\mathrm{tan}\:\varphi=\frac{{a}}{{b}}\mathrm{tan}\:\phi=\frac{\mathrm{tan}\:\phi}{\lambda} \\ $$$$\mathrm{tan}\:\beta=\frac{{b}\:\mathrm{sin}\:\phi}{{c}−{a}\:\mathrm{cos}\:\phi}=\frac{\lambda\:\mathrm{sin}\:\phi}{\mu−\mathrm{cos}\:\phi} \\ $$$$\alpha=\varphi−\frac{\theta}{\mathrm{2}}\:\Rightarrow\theta=\mathrm{2}\varphi−\mathrm{2}\alpha \\ $$$$\beta=\pi−\alpha−\theta\:\Rightarrow\beta=\pi−\mathrm{2}\varphi+\alpha \\ $$$$\Rightarrow\mathrm{2}\varphi=\pi−\left(\beta−\alpha\right) \\ $$$$\Rightarrow\mathrm{tan}\:\mathrm{2}\varphi=\mathrm{tan}\:\left(\alpha−\beta\right) \\ $$$$\Rightarrow\frac{\frac{\mathrm{2}\:\mathrm{tan}\:\phi}{\lambda}}{\mathrm{1}−\frac{\mathrm{tan}^{\mathrm{2}} \:\phi}{\lambda^{\mathrm{2}} }}=\frac{\lambda\:\mathrm{tan}\:\phi−\frac{\lambda\:\mathrm{sin}\:\phi}{\mu−\mathrm{cos}\:\phi}}{\mathrm{1}+\lambda\:\mathrm{tan}\:\phi×\frac{\lambda\:\mathrm{sin}\:\phi}{\mu−\mathrm{cos}\:\phi}} \\ $$$$\Rightarrow\frac{\mathrm{2}\:\mathrm{tan}\:\phi}{\lambda^{\mathrm{2}} −\mathrm{tan}^{\mathrm{2}} \:\phi}=\frac{\mathrm{tan}\:\phi\left(\mu−\mathrm{cos}\:\phi\right)−\mathrm{sin}\:\phi}{\mu−\mathrm{cos}\:\phi+\lambda^{\mathrm{2}} \:\mathrm{sin}\:\phi\:\mathrm{tan}\:\phi} \\ $$$$\Rightarrow\frac{\mathrm{2}\:\mathrm{cos}\:\phi}{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\phi−\mathrm{1}}=\frac{\mu−\mathrm{2}\:\mathrm{cos}\:\phi}{\lambda^{\mathrm{2}} +\mu\:\mathrm{cos}\:\phi−\left(\mathrm{1}+\lambda^{\mathrm{2}} \right)\mathrm{cos}^{\mathrm{2}} \:\phi} \\ $$$${let}\:{t}=\mathrm{cos}\:\phi \\ $$$$\Rightarrow\frac{\mathrm{2}{t}}{\left(\mathrm{1}+\lambda^{\mathrm{2}} \right){t}^{\mathrm{2}} −\mathrm{1}}=\frac{\mu−\mathrm{2}{t}}{\lambda^{\mathrm{2}} +\mu{t}−\left(\mathrm{1}+\lambda^{\mathrm{2}} \right){t}^{\mathrm{2}} } \\ $$$$\Rightarrow{t}^{\mathrm{2}} \:−\frac{\mathrm{2}}{\mu}{t}+\frac{\mathrm{1}}{\mathrm{1}−\lambda^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{\mu}−\sqrt{\frac{\mathrm{1}}{\mu^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}−\lambda^{\mathrm{2}} }} \\ $$$$\Rightarrow\phi=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mu}−\sqrt{\frac{\mathrm{1}}{\mu^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}−\lambda^{\mathrm{2}} }}\right) \\ $$$$\Rightarrow\theta_{{max}} =\mathrm{2}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\phi}{\lambda}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\lambda\:\mathrm{tan}\:\phi\right)\right] \\ $$$${example}: \\ $$$$\lambda=\frac{{b}}{{a}}=\frac{\mathrm{2}}{\mathrm{3}},\:\mu=\frac{{c}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{t}=\mathrm{2}−\sqrt{\frac{\mathrm{11}}{\mathrm{5}}} \\ $$$$\Rightarrow\phi=\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{2}−\sqrt{\frac{\mathrm{11}}{\mathrm{5}}}\right)=\mathrm{58}.\mathrm{8845}° \\ $$$$\Rightarrow\alpha=\mathrm{47}.\mathrm{8429}° \\ $$$$\Rightarrow\varphi=\mathrm{68}.\mathrm{0799}° \\ $$$$\Rightarrow\beta=\mathrm{91}.\mathrm{6831}° \\ $$$$\Rightarrow\theta_{{max}} =\mathrm{2}\left(\mathrm{68}.\mathrm{0799}−\mathrm{47}.\mathrm{8429}\right)=\mathrm{40}.\mathrm{474}° \\ $$
Commented by ajfour last updated on 28/Nov/19
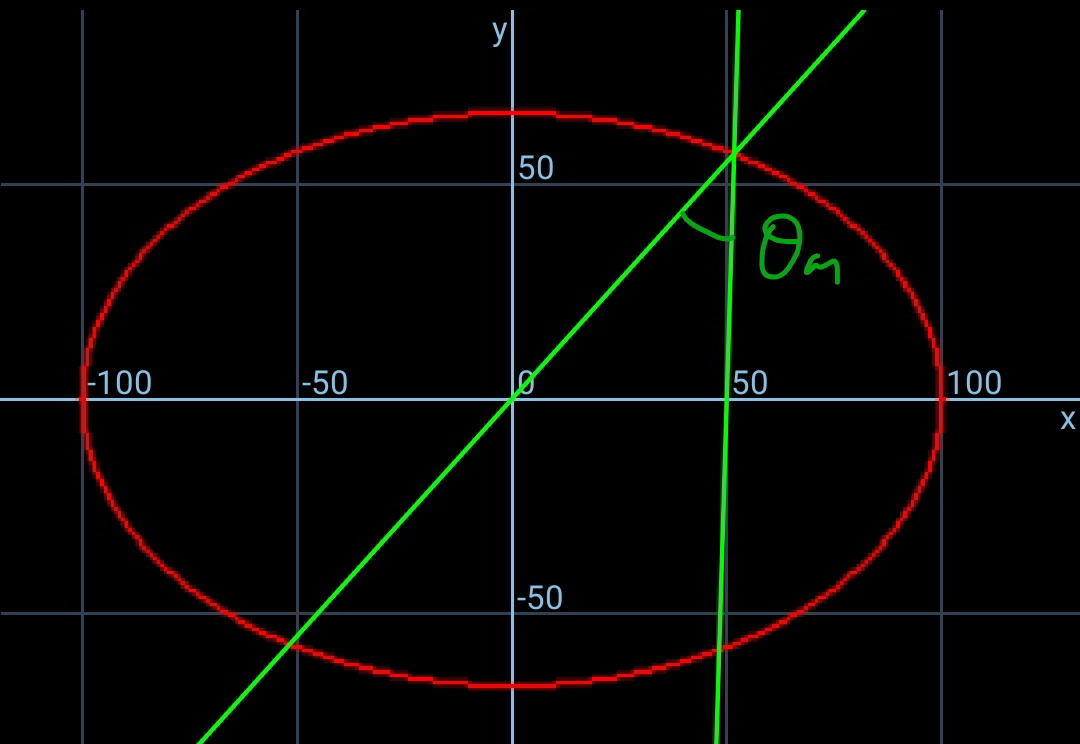
$${Thank}\:{you}\:{Sir}.\:{I}\:{also}\:{get}\:{near} \\ $$$${around}\:{the}\:{same}\:{value}. \\ $$
Commented by mr W last updated on 29/Nov/19

$${thanks}\:{sir}! \\ $$$${i}\:{am}\:{not}\:{sure}\:{if}\:{i}\:{am}\:{right}.\:{i}\:{think} \\ $$$${P}\:{should}\:{be}\:{the}\:{reflection}\:{point}\:{for} \\ $$$${a}\:{light}\:{ray}\:{from}\:{O}\:{to}\:{F}\:{when}\:\theta\:{is} \\ $$$${maximum}.\:{but}\:{for}\:{some}\:{large}\:{values} \\ $$$${of}\:{c}\:\left({e}.{g}.\:{c}={a}\right)\:{there}\:{is}\:{no}\:{such}\:{point} \\ $$$${P}.\:\:{this}\:{can}\:{be}\:{seen}\:{in}\:{my}\:{formula}\:{for} \\ $$$$\phi.\:{we}\:{get}\:{condition}\:\mu\leqslant\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$
Commented by ajfour last updated on 29/Nov/19
$${yes}\:{sir},\:{seems}\:{likely}! \\ $$
