Question Number 74697 by chess1 last updated on 29/Nov/19
Answered by mr W last updated on 29/Nov/19

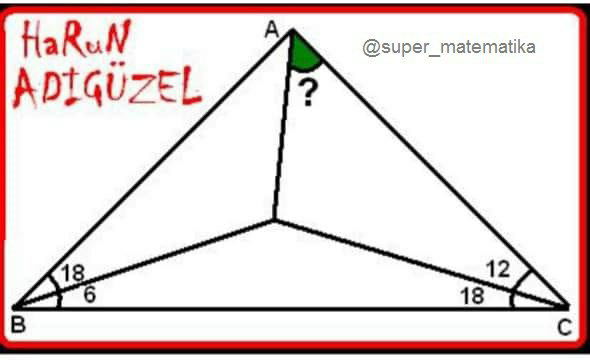
$${let}\:{BC}=\mathrm{1} \\ $$$${DC}=\frac{\mathrm{sin}\:\mathrm{6}}{\mathrm{sin}\:\mathrm{24}} \\ $$$${AC}=\frac{\mathrm{sin}\:\mathrm{24}}{\mathrm{sin}\:\mathrm{54}} \\ $$$$\frac{\mathrm{sin}\:\left(\mathrm{12}+{x}\right)}{\mathrm{sin}\:{x}}=\frac{\mathrm{sin}\:\mathrm{24}×\mathrm{sin}\:\mathrm{24}}{\mathrm{sin}\:\mathrm{54}×\mathrm{sin}\:\mathrm{6}} \\ $$$$\frac{\mathrm{sin}\:\mathrm{12}}{\mathrm{tan}\:{x}}+\mathrm{cos}\:\mathrm{12}=\frac{\mathrm{sin}\:\mathrm{24}×\mathrm{sin}\:\mathrm{24}}{\mathrm{sin}\:\mathrm{54}×\mathrm{sin}\:\mathrm{6}} \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{sin}\:\mathrm{12}}{\frac{\mathrm{sin}\:\mathrm{24}×\mathrm{sin}\:\mathrm{24}}{\mathrm{sin}\:\mathrm{54}×\mathrm{sin}\:\mathrm{6}}−\mathrm{cos}\:\mathrm{12}} \\ $$$$\Rightarrow{x}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{sin}\:\mathrm{12}}{\frac{\mathrm{sin}\:\mathrm{24}×\mathrm{sin}\:\mathrm{24}}{\mathrm{sin}\:\mathrm{54}×\mathrm{sin}\:\mathrm{6}}−\mathrm{cos}\:\mathrm{12}}\right)=\mathrm{12}° \\ $$
Commented by chess1 last updated on 29/Nov/19

$$\mathrm{thanks} \\ $$
