Question Number 74698 by ajfour last updated on 29/Nov/19
Commented by ajfour last updated on 29/Nov/19
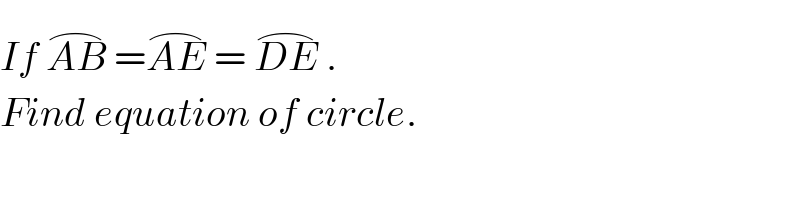
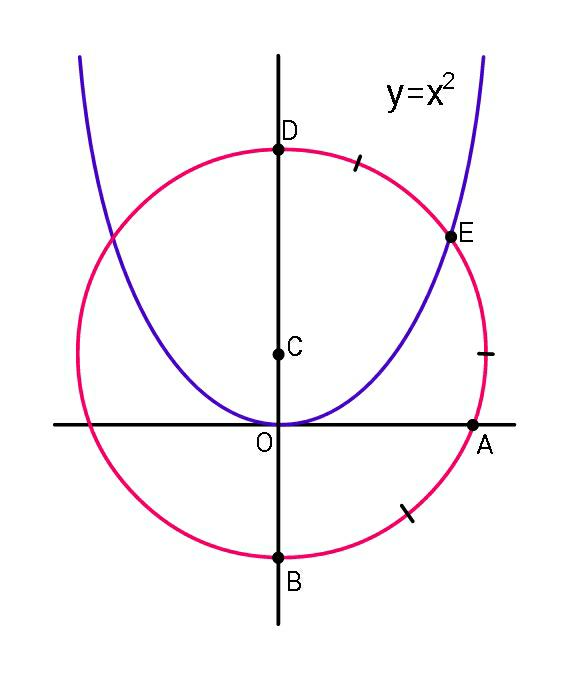
$${If}\:\overset{\frown} {{AB}}\:=\overset{\frown} {{AE}}\:=\:\overset{\frown} {{DE}}\:. \\ $$$${Find}\:{equation}\:{of}\:{circle}. \\ $$
Answered by ajfour last updated on 29/Nov/19
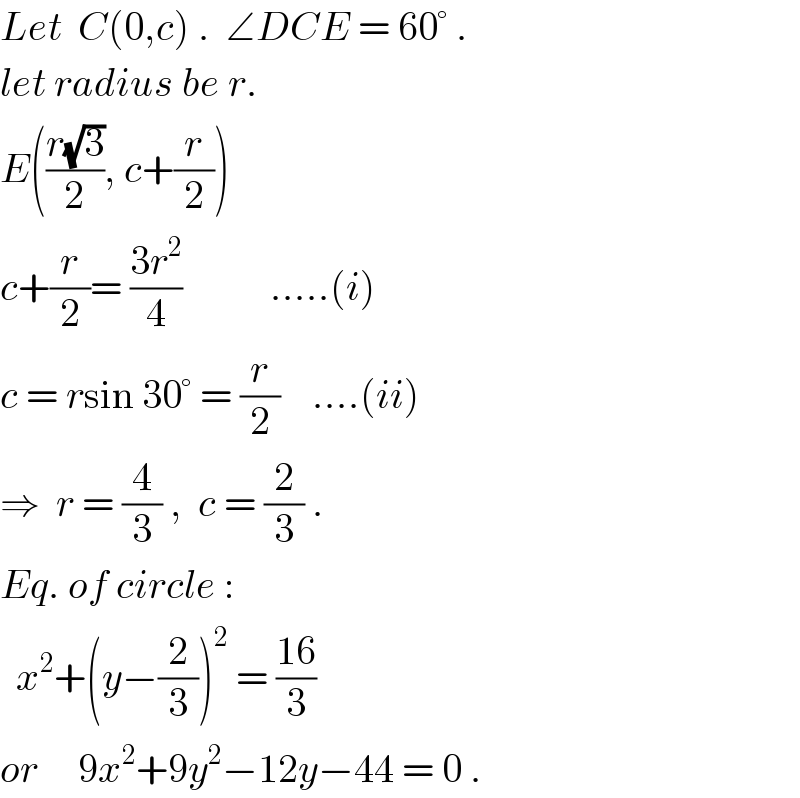
$${Let}\:\:{C}\left(\mathrm{0},{c}\right)\:.\:\:\angle{DCE}\:=\:\mathrm{60}°\:. \\ $$$${let}\:{radius}\:{be}\:{r}. \\ $$$${E}\left(\frac{{r}\sqrt{\mathrm{3}}}{\mathrm{2}},\:{c}+\frac{{r}}{\mathrm{2}}\right) \\ $$$${c}+\frac{{r}}{\mathrm{2}}=\:\frac{\mathrm{3}{r}^{\mathrm{2}} }{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:…..\left({i}\right) \\ $$$${c}\:=\:{r}\mathrm{sin}\:\mathrm{30}°\:=\:\frac{{r}}{\mathrm{2}}\:\:\:\:….\left({ii}\right) \\ $$$$\Rightarrow\:\:{r}\:=\:\frac{\mathrm{4}}{\mathrm{3}}\:,\:\:{c}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\:. \\ $$$${Eq}.\:{of}\:{circle}\:: \\ $$$$\:\:{x}^{\mathrm{2}} +\left({y}−\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{16}}{\mathrm{3}} \\ $$$${or}\:\:\:\:\:\mathrm{9}{x}^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} −\mathrm{12}{y}−\mathrm{44}\:=\:\mathrm{0}\:. \\ $$
Answered by mind is power last updated on 29/Nov/19
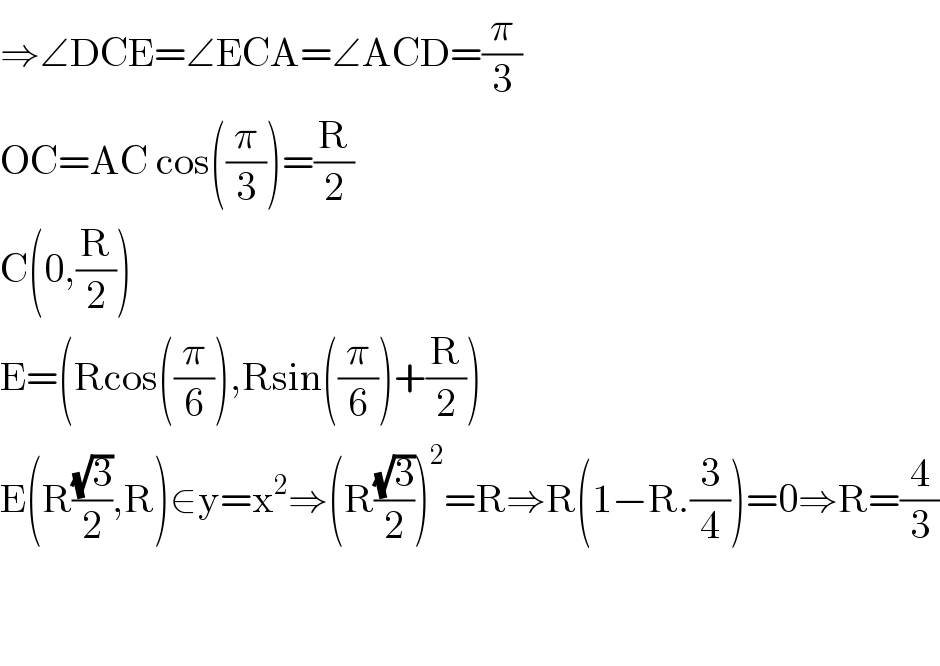
$$\Rightarrow\angle\mathrm{DCE}=\angle\mathrm{ECA}=\angle\mathrm{ACD}=\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{OC}=\mathrm{AC}\:\mathrm{cos}\left(\frac{\pi}{\mathrm{3}}\right)=\frac{\mathrm{R}}{\mathrm{2}} \\ $$$$\mathrm{C}\left(\mathrm{0},\frac{\mathrm{R}}{\mathrm{2}}\right) \\ $$$$\mathrm{E}=\left(\mathrm{Rcos}\left(\frac{\pi}{\mathrm{6}}\right),\mathrm{Rsin}\left(\frac{\pi}{\mathrm{6}}\right)+\frac{\mathrm{R}}{\mathrm{2}}\right) \\ $$$$\mathrm{E}\left(\mathrm{R}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}},\mathrm{R}\right)\in\mathrm{y}=\mathrm{x}^{\mathrm{2}} \Rightarrow\left(\mathrm{R}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{R}\Rightarrow\mathrm{R}\left(\mathrm{1}−\mathrm{R}.\frac{\mathrm{3}}{\mathrm{4}}\right)=\mathrm{0}\Rightarrow\mathrm{R}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$
