Question Number 74712 by aliesam last updated on 29/Nov/19

Commented by MJS last updated on 29/Nov/19
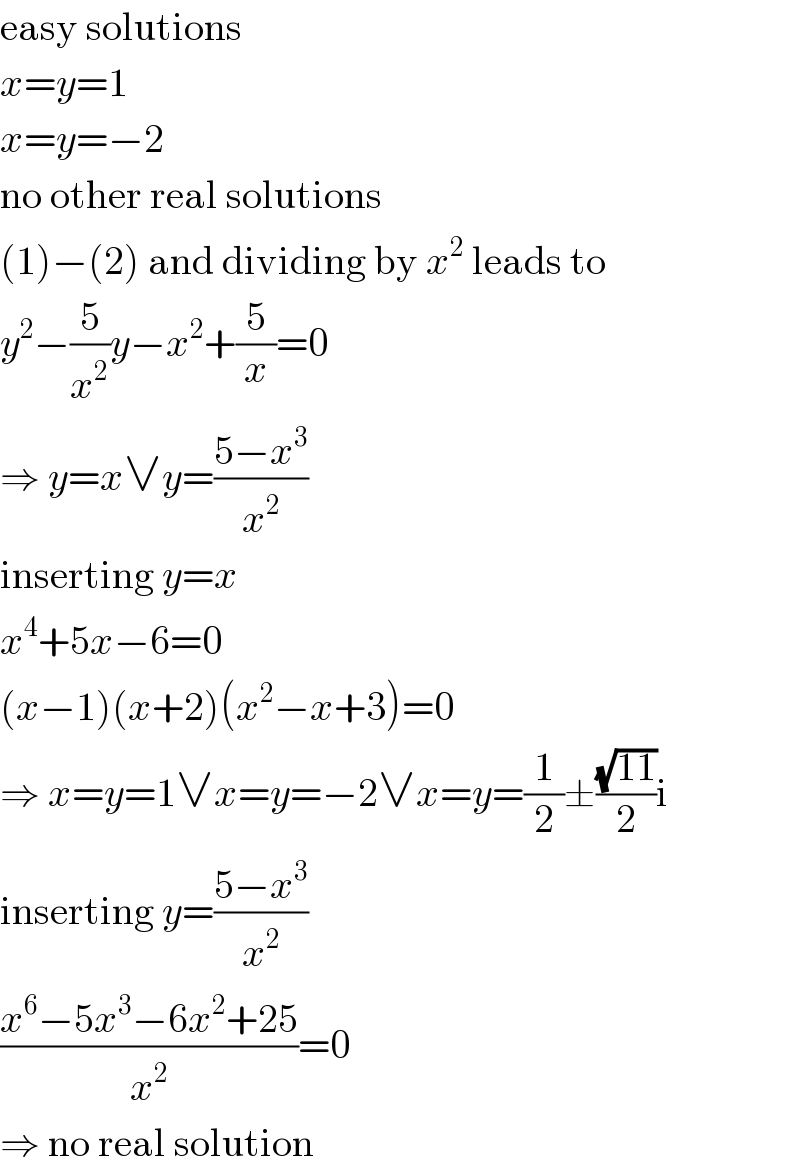
$$\mathrm{easy}\:\mathrm{solutions} \\ $$$${x}={y}=\mathrm{1} \\ $$$${x}={y}=−\mathrm{2} \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\:\mathrm{and}\:\mathrm{dividing}\:\mathrm{by}\:{x}^{\mathrm{2}} \:\mathrm{leads}\:\mathrm{to} \\ $$$${y}^{\mathrm{2}} −\frac{\mathrm{5}}{{x}^{\mathrm{2}} }{y}−{x}^{\mathrm{2}} +\frac{\mathrm{5}}{{x}}=\mathrm{0} \\ $$$$\Rightarrow\:{y}={x}\vee{y}=\frac{\mathrm{5}−{x}^{\mathrm{3}} }{{x}^{\mathrm{2}} } \\ $$$$\mathrm{inserting}\:{y}={x} \\ $$$${x}^{\mathrm{4}} +\mathrm{5}{x}−\mathrm{6}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}={y}=\mathrm{1}\vee{x}={y}=−\mathrm{2}\vee{x}={y}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{inserting}\:{y}=\frac{\mathrm{5}−{x}^{\mathrm{3}} }{{x}^{\mathrm{2}} } \\ $$$$\frac{{x}^{\mathrm{6}} −\mathrm{5}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{25}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{real}\:\mathrm{solution} \\ $$
Commented by aliesam last updated on 30/Nov/19

$${thank}\:{you}\:{sir}\:{but}\:{i}\:{have}\:{tow}\:{questions} \\ $$$$ \\ $$$$\left.\mathrm{1}\right){can}\:{we}\:{solve}\:{the}\:{first}\:{equation}\:{without}\:{using}\:{rational}\:{root}\:{theorm}\: \\ $$$$ \\ $$$$\left.\mathrm{2}\right){how}\:{did}\:{you}\:{now}\:{that}\:{the}\:{second}\:{equation}\:{has}\:{no}\:{solution}\:{in}\:{R} \\ $$$$ \\ $$$${and}\:{thank}\:{you}\:{very}\:{much} \\ $$$$ \\ $$
