Question-74726

Question Number 74726 by ajfour last updated on 29/Nov/19

Commented by ajfour last updated on 29/Nov/19

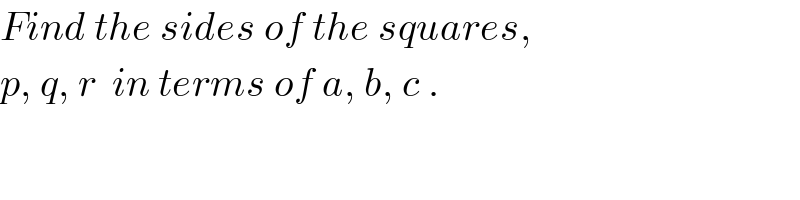
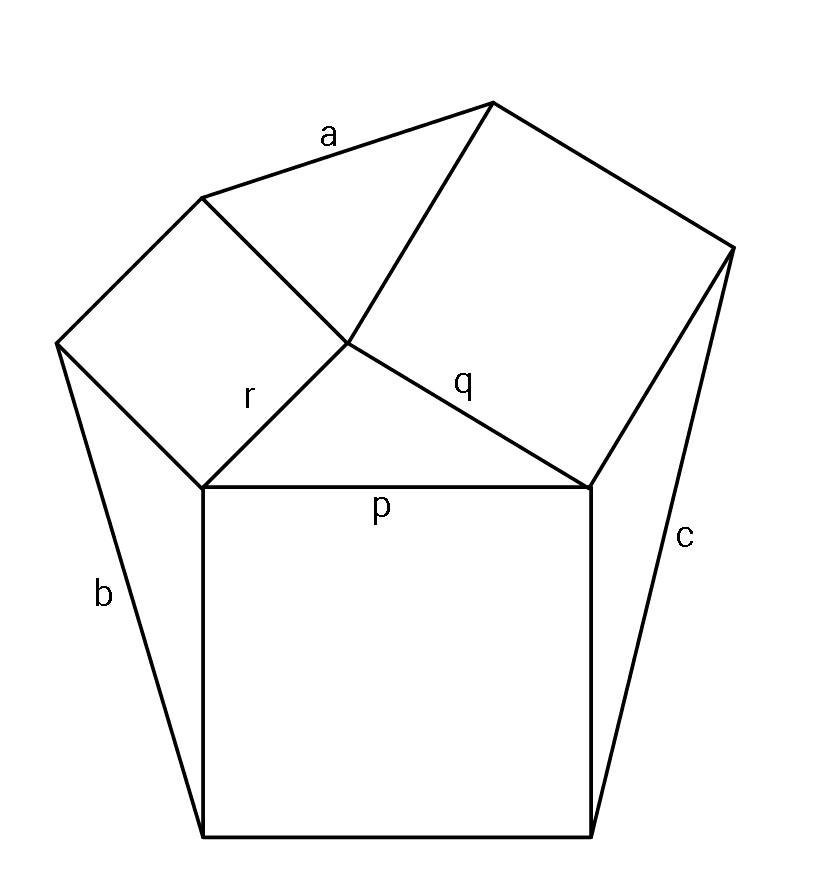
$${Find}\:{the}\:{sides}\:{of}\:{the}\:{squares}, \\ $$$${p},\:{q},\:{r}\:\:{in}\:{terms}\:{of}\:{a},\:{b},\:{c}\:. \\ $$

Commented by mr W last updated on 29/Nov/19

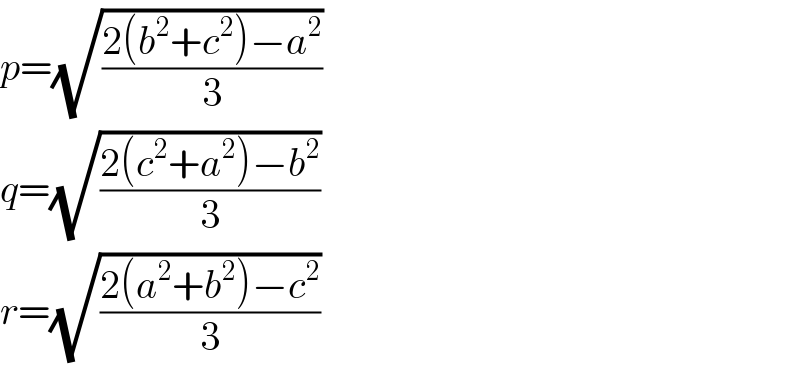
p=(√((2(b^2 +c^2 )−a^2 )/3)) q=(√((2(c^2 +a^2 )−b^2 )/3)) r=(√((2(a^2 +b^2 )−c^2 )/3))

$${p}=\sqrt{\frac{\mathrm{2}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} }{\mathrm{3}}} \\ $$$${q}=\sqrt{\frac{\mathrm{2}\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} }{\mathrm{3}}} \\ $$$${r}=\sqrt{\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} }{\mathrm{3}}} \\ $$

Commented by ajfour last updated on 29/Nov/19

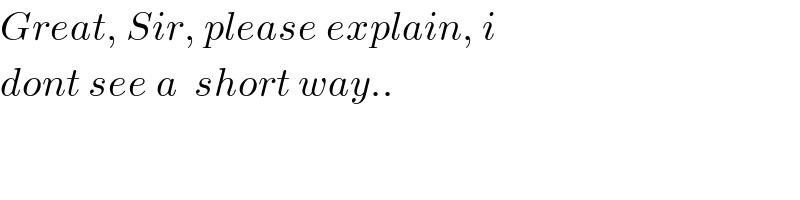
$${Great},\:{Sir},\:{please}\:{explain},\:{i} \\ $$$${dont}\:{see}\:{a}\:\:{short}\:{way}.. \\ $$

Answered by mr W last updated on 29/Nov/19

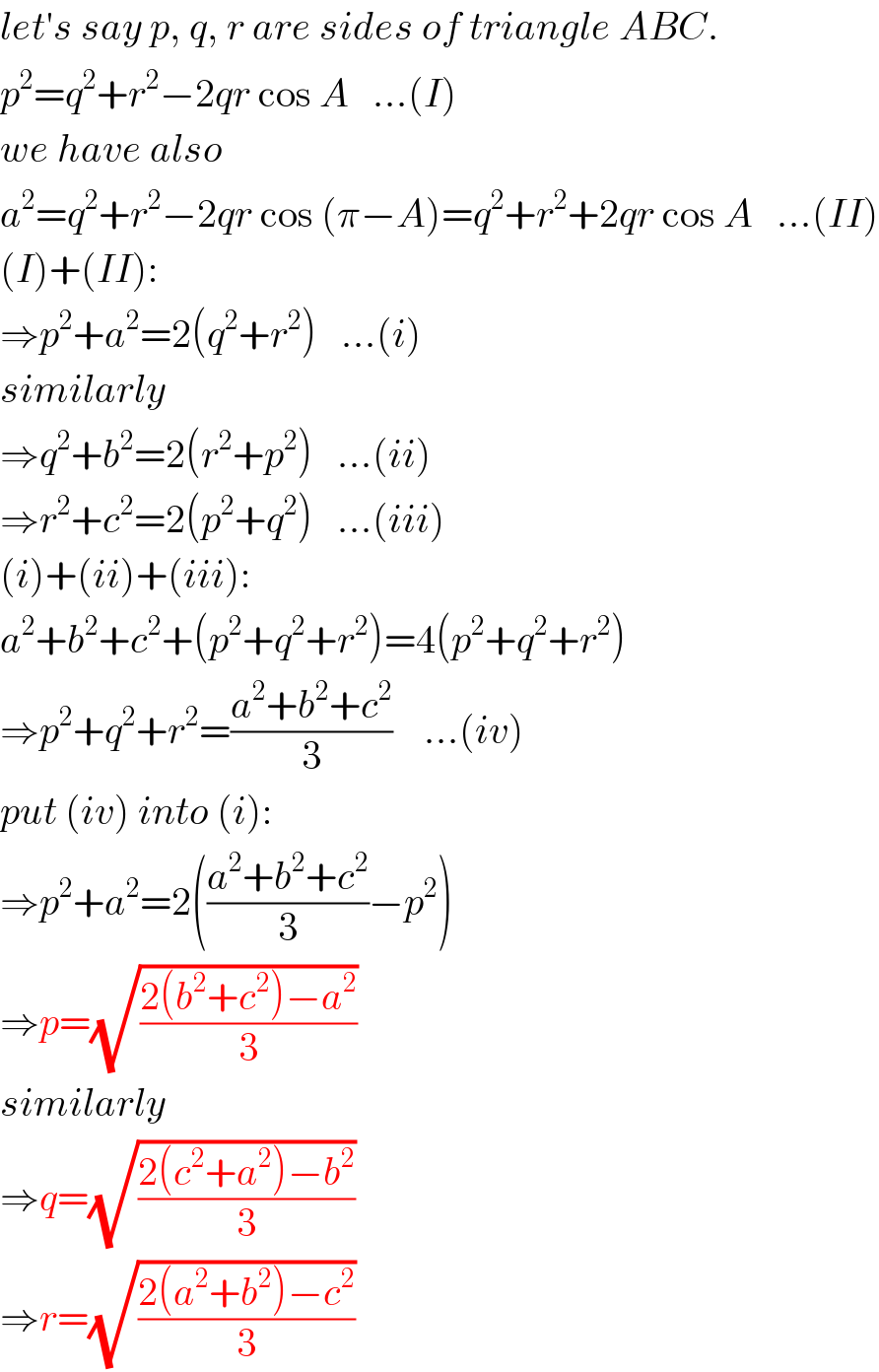
let′s say p, q, r are sides of triangle ABC. p^2 =q^2 +r^2 −2qr cos A ...(I) we have also a^2 =q^2 +r^2 −2qr cos (π−A)=q^2 +r^2 +2qr cos A ...(II) (I)+(II): ⇒p^2 +a^2 =2(q^2 +r^2 ) ...(i) similarly ⇒q^2 +b^2 =2(r^2 +p^2 ) ...(ii) ⇒r^2 +c^2 =2(p^2 +q^2 ) ...(iii) (i)+(ii)+(iii): a^2 +b^2 +c^2 +(p^2 +q^2 +r^2 )=4(p^2 +q^2 +r^2 ) ⇒p^2 +q^2 +r^2 =((a^2 +b^2 +c^2 )/3) ...(iv) put (iv) into (i): ⇒p^2 +a^2 =2(((a^2 +b^2 +c^2 )/3)−p^2 ) ⇒p=(√((2(b^2 +c^2 )−a^2 )/3)) similarly ⇒q=(√((2(c^2 +a^2 )−b^2 )/3)) ⇒r=(√((2(a^2 +b^2 )−c^2 )/3))

$${let}'{s}\:{say}\:{p},\:{q},\:{r}\:{are}\:{sides}\:{of}\:{triangle}\:{ABC}.\: \\ $$$${p}^{\mathrm{2}} ={q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{qr}\:\mathrm{cos}\:{A}\:\:\:…\left({I}\right) \\ $$$${we}\:{have}\:{also} \\ $$$${a}^{\mathrm{2}} ={q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{qr}\:\mathrm{cos}\:\left(\pi−{A}\right)={q}^{\mathrm{2}} +{r}^{\mathrm{2}} +\mathrm{2}{qr}\:\mathrm{cos}\:{A}\:\:\:…\left({II}\right) \\ $$$$\left({I}\right)+\left({II}\right): \\ $$$$\Rightarrow{p}^{\mathrm{2}} +{a}^{\mathrm{2}} =\mathrm{2}\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)\:\:\:…\left({i}\right) \\ $$$${similarly} \\ $$$$\Rightarrow{q}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{2}\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow{r}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)\:\:\:…\left({iii}\right) \\ $$$$\left({i}\right)+\left({ii}\right)+\left({iii}\right): \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)=\mathrm{4}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}\:\:\:\:…\left({iv}\right) \\ $$$${put}\:\left({iv}\right)\:{into}\:\left({i}\right): \\ $$$$\Rightarrow{p}^{\mathrm{2}} +{a}^{\mathrm{2}} =\mathrm{2}\left(\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}}−{p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{p}=\sqrt{\frac{\mathrm{2}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} }{\mathrm{3}}} \\ $$$${similarly} \\ $$$$\Rightarrow{q}=\sqrt{\frac{\mathrm{2}\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} }{\mathrm{3}}} \\ $$$$\Rightarrow{r}=\sqrt{\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} }{\mathrm{3}}} \\ $$

Commented by ajfour last updated on 29/Nov/19

$${Wonderful},\:{Sir}.\:{I}\:{could}\:{have} \\ $$$${solved}\:{it}\:{had}\:{i}\:{proceeded}, \\ $$$${you}\:{put}\:{it}\:{in}\:{nice}\:{details},\:{sir}. \\ $$$${Thanks}. \\ $$

Commented by mr W last updated on 30/Nov/19

$${i}'{m}\:{sure}\:{you}\:{would}\:{come}\:{to}\:{the}\:{same} \\ $$$${solution}\:{sir}. \\ $$$${inspired}\:{by}\:{this}\:{question}\:{i}\:{have}\:{created} \\ $$$${a}\:{new}\:{question}\:{about}\:{the}\:{areas}\:{of}\:{the} \\ $$$${squares}.\:{please}\:{give}\:{a}\:{try}\:{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply