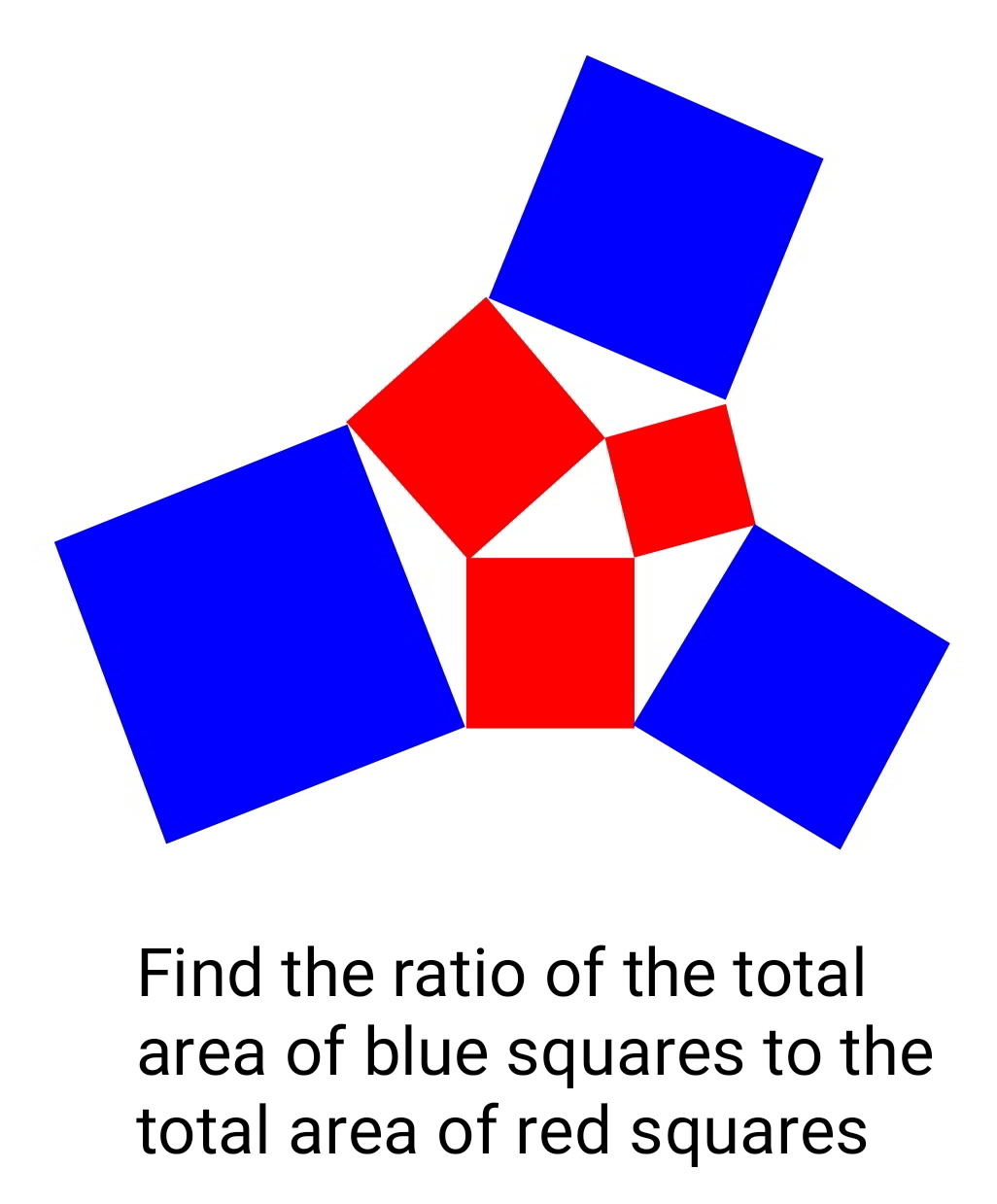
Question Number 74747 by mr W last updated on 30/Nov/19
Answered by mind is power last updated on 30/Nov/19

$$\mathrm{let}\:\mathrm{p},\mathrm{q},\mathrm{r}\:\mathrm{side}\:\mathrm{of}\:\mathrm{red}\:\mathrm{squar},\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{blue} \\ $$$$\alpha,\beta,\varsigma\:\:\mathrm{angle}\:\mathrm{thetriangl}\:\mathrm{inside}\:\mathrm{red}\:\mathrm{squar} \\ $$$$\mathrm{a}^{\mathrm{2}} =\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{2pqcos}\left(\alpha\right) \\ $$$$\mathrm{b}^{\mathrm{2}} =\mathrm{p}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} +\mathrm{2prcos}\left(\beta\right) \\ $$$$\mathrm{c}^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{2rqcos}\left(\varsigma\right) \\ $$$$\mathrm{cos}\left(\alpha\right)=\frac{\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} }{\mathrm{2pq}},\mathrm{cos}\left(\beta\right)=\frac{\mathrm{p}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} −\mathrm{q}^{\mathrm{2}} }{\mathrm{2pr}} \\ $$$$\mathrm{cos}\left(\varsigma\right)=\frac{\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} −\mathrm{p}^{\mathrm{2}} }{\mathrm{2qr}} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{2p}^{\mathrm{2}} +\mathrm{2q}^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} ,\mathrm{b}^{\mathrm{2}} =\mathrm{2p}^{\mathrm{2}} +\mathrm{2r}^{\mathrm{2}} −\mathrm{q}^{\mathrm{2}} ,\mathrm{c}^{\mathrm{2}} =\mathrm{2r}^{\mathrm{2}} +\mathrm{2q}^{\mathrm{2}} −\mathrm{p}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{3}\left(\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} }{\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} }=\mathrm{3} \\ $$$$ \\ $$
Commented by mr W last updated on 30/Nov/19
$${thanks}\:{sir}! \\ $$$${i}\:{got}\:{the}\:{same}\:{result}\:{in}\:{Q}\mathrm{74726}. \\ $$
Commented by mind is power last updated on 30/Nov/19

$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom}\: \\ $$
