Question Number 74748 by mr W last updated on 30/Nov/19

Commented by mr W last updated on 30/Nov/19

$${If}\:{the}\:{total}\:{area}\:{of}\:{red}\:{squares}\:{is}\:{A}. \\ $$$${Find}\:{the}\:{total}\:{area}\:{of}\:{the}\:{blue}\:{squares} \\ $$$${and}\:{that}\:{of}\:{the}\:{green}\:{squares}. \\ $$$$ \\ $$$${Can}\:{this}\:{be}\:{generalised}\:{further}\:{for}\:{the} \\ $$$${orange}\:{squares}\:{as}\:{following}\:{and}\:{so}\:{on} \\ $$$${to}\:{the}\:{n}−{th}\:{level}\:{squares}? \\ $$
Commented by mr W last updated on 30/Nov/19

Commented by ajfour last updated on 30/Nov/19
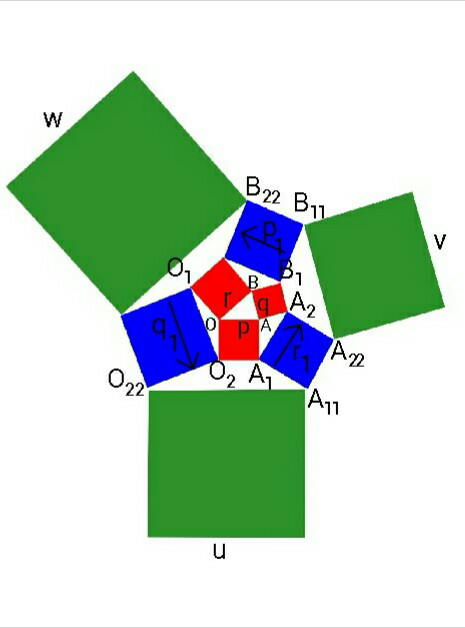
Answered by ajfour last updated on 30/Nov/19
![O(0,0) , A(1,0) , B(rcos θ, rsin θ) let p=OA=1 q^2 = (−rcos θ+1)^2 +r^2 sin^2 θ qsin φ=rsin θ △_0 = 1+r^2 +1+r^2 −2rcos θ = 2+2r(r−cos θ) O_1 =(−rsin θ, rcos θ) O_2 =(0,−1) A_1 =(1,−1) A_2 =(1+rsin θ, 1−rcos θ) B_1 =(rcos θ+rsin θ, 1+rsin θ−rcos θ) B_2 =(rcos θ−rsin θ, rsin θ+rcos θ) q_1 ^2 =(O_1 O_2 )^2 = (1+rcos θ)^2 +r^2 sin^2 θ r_1 ^2 =(A_1 A_2 )^2 = (2−rcos θ)^2 +r^2 sin^2 θ p_1 ^2 =(B_1 B_2 )^2 =4r^2 sin^2 θ+(2rcos θ−1)^2 △_1 = p_1 ^2 +q_1 ^2 +r_1 ^2 = 6+6r(r−cos θ) ⇒ △_1 = 6+3(△_0 −2) = 3△_0 ________________________ p_1 ^� =−2rsin θ+i(2rcos θ−1) q_1 ^� = rsin θ−i(1+rcos θ) r_1 ^� = rsin θ+i(2−rcos θ) A_(11) = A_1 −ir_1 ^� = 1−i−i[rsin θ+i(2−rcos θ)] = 3−rcos θ−i(1+rsin θ) O_(22) = O_2 −iq_1 ^� = −i−i[rsin θ−i(1+rcos θ)] = −(1+rcos θ)−i(1+rsin θ) u= O_(22) A_(11) = 4 = 4p A_(22) =A_2 −ir_1 ^� = 1+rsin θ+i(1−rcos θ) −i[rsin θ+i(2−rcos θ)] = 3+rsin θ−rcos θ +i(1−rcos θ−rsin θ) B_(11) =B_1 −ip_1 ^� = rcos θ+rsin θ+i(1+rsin θ−rcos θ) −i[−2rsin θ+i(2rcos θ−1)] = 3rcos θ−1+rsin θ+i(1+3rsin θ−rcos θ) v=A_(22) B_(11) =4rcos θ−4+i(4rsin θ) ∣A_(22) B_(11) ∣=4(√(1+r(r−2cos θ))) ((∣A_(22) B_(11) ∣)/q)=((4(√(1+r(r−2cos θ))))/( (√(1+r(r−2cos θ))))) = 4 ⇒ v= 4q similary w= B_(22) O_(11) = 4r ⇒ Sum of areas of green squares = △_2 = u^2 +v^2 +w^2 = 16(p^2 +q^2 +r^2 ) = 16△_0 .](https://www.tinkutara.com/question/Q74781.png)
$${O}\left(\mathrm{0},\mathrm{0}\right)\:\:,\:{A}\left(\mathrm{1},\mathrm{0}\right)\:,\:{B}\left({r}\mathrm{cos}\:\theta,\:{r}\mathrm{sin}\:\theta\right) \\ $$$${let}\:\:{p}={OA}=\mathrm{1} \\ $$$${q}^{\mathrm{2}} =\:\left(−{r}\mathrm{cos}\:\theta+\mathrm{1}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${q}\mathrm{sin}\:\phi={r}\mathrm{sin}\:\theta \\ $$$$\bigtriangleup_{\mathrm{0}} =\:\mathrm{1}+{r}^{\mathrm{2}} +\mathrm{1}+{r}^{\mathrm{2}} −\mathrm{2}{r}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:=\:\mathrm{2}+\mathrm{2}{r}\left({r}−\mathrm{cos}\:\theta\right) \\ $$$${O}_{\mathrm{1}} =\left(−{r}\mathrm{sin}\:\theta,\:{r}\mathrm{cos}\:\theta\right) \\ $$$${O}_{\mathrm{2}} =\left(\mathrm{0},−\mathrm{1}\right)\:\: \\ $$$${A}_{\mathrm{1}} =\left(\mathrm{1},−\mathrm{1}\right) \\ $$$${A}_{\mathrm{2}} =\left(\mathrm{1}+{r}\mathrm{sin}\:\theta,\:\mathrm{1}−{r}\mathrm{cos}\:\theta\right) \\ $$$${B}_{\mathrm{1}} =\left({r}\mathrm{cos}\:\theta+{r}\mathrm{sin}\:\theta,\:\mathrm{1}+{r}\mathrm{sin}\:\theta−{r}\mathrm{cos}\:\theta\right) \\ $$$${B}_{\mathrm{2}} =\left({r}\mathrm{cos}\:\theta−{r}\mathrm{sin}\:\theta,\:{r}\mathrm{sin}\:\theta+{r}\mathrm{cos}\:\theta\right) \\ $$$${q}_{\mathrm{1}} ^{\mathrm{2}} =\left({O}_{\mathrm{1}} {O}_{\mathrm{2}} \right)^{\mathrm{2}} =\:\left(\mathrm{1}+{r}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${r}_{\mathrm{1}} ^{\mathrm{2}} =\left({A}_{\mathrm{1}} {A}_{\mathrm{2}} \right)^{\mathrm{2}} =\:\left(\mathrm{2}−{r}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta \\ $$$${p}_{\mathrm{1}} ^{\mathrm{2}} =\left({B}_{\mathrm{1}} {B}_{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta+\left(\mathrm{2}{r}\mathrm{cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\bigtriangleup_{\mathrm{1}} =\:{p}_{\mathrm{1}} ^{\mathrm{2}} +{q}_{\mathrm{1}} ^{\mathrm{2}} +{r}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\:\mathrm{6}+\mathrm{6}{r}\left({r}−\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\:\bigtriangleup_{\mathrm{1}} =\:\mathrm{6}+\mathrm{3}\left(\bigtriangleup_{\mathrm{0}} −\mathrm{2}\right)\:=\:\mathrm{3}\bigtriangleup_{\mathrm{0}} \:\: \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$$\bar {{p}}_{\mathrm{1}} =−\mathrm{2}{r}\mathrm{sin}\:\theta+{i}\left(\mathrm{2}{r}\mathrm{cos}\:\theta−\mathrm{1}\right) \\ $$$$\bar {{q}}_{\mathrm{1}} =\:{r}\mathrm{sin}\:\theta−{i}\left(\mathrm{1}+{r}\mathrm{cos}\:\theta\right) \\ $$$$\bar {{r}}_{\mathrm{1}} =\:{r}\mathrm{sin}\:\theta+{i}\left(\mathrm{2}−{r}\mathrm{cos}\:\theta\right) \\ $$$${A}_{\mathrm{11}} =\:{A}_{\mathrm{1}} −{i}\bar {{r}}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:=\:\mathrm{1}−{i}−{i}\left[{r}\mathrm{sin}\:\theta+{i}\left(\mathrm{2}−{r}\mathrm{cos}\:\theta\right)\right] \\ $$$$\:\:\:\:\:=\:\mathrm{3}−{r}\mathrm{cos}\:\theta−{i}\left(\mathrm{1}+{r}\mathrm{sin}\:\theta\right) \\ $$$${O}_{\mathrm{22}} =\:{O}_{\mathrm{2}} −{i}\bar {{q}}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:=\:−{i}−{i}\left[{r}\mathrm{sin}\:\theta−{i}\left(\mathrm{1}+{r}\mathrm{cos}\:\theta\right)\right] \\ $$$$\:\:\:\:\:\:\:=\:−\left(\mathrm{1}+{r}\mathrm{cos}\:\theta\right)−{i}\left(\mathrm{1}+{r}\mathrm{sin}\:\theta\right) \\ $$$${u}=\:{O}_{\mathrm{22}} {A}_{\mathrm{11}} =\:\mathrm{4}\:=\:\mathrm{4}{p} \\ $$$${A}_{\mathrm{22}} ={A}_{\mathrm{2}} −{i}\bar {{r}}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{1}+{r}\mathrm{sin}\:\theta+{i}\left(\mathrm{1}−{r}\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:−{i}\left[{r}\mathrm{sin}\:\theta+{i}\left(\mathrm{2}−{r}\mathrm{cos}\:\theta\right)\right] \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{3}+{r}\mathrm{sin}\:\theta−{r}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{i}\left(\mathrm{1}−{r}\mathrm{cos}\:\theta−{r}\mathrm{sin}\:\theta\right) \\ $$$${B}_{\mathrm{11}} ={B}_{\mathrm{1}} −{i}\bar {{p}}_{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:=\:{r}\mathrm{cos}\:\theta+{r}\mathrm{sin}\:\theta+{i}\left(\mathrm{1}+{r}\mathrm{sin}\:\theta−{r}\mathrm{cos}\:\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:−{i}\left[−\mathrm{2}{r}\mathrm{sin}\:\theta+{i}\left(\mathrm{2}{r}\mathrm{cos}\:\theta−\mathrm{1}\right)\right] \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{3}{r}\mathrm{cos}\:\theta−\mathrm{1}+{r}\mathrm{sin}\:\theta+{i}\left(\mathrm{1}+\mathrm{3}{r}\mathrm{sin}\:\theta−{r}\mathrm{cos}\:\theta\right) \\ $$$${v}={A}_{\mathrm{22}} {B}_{\mathrm{11}} =\mathrm{4}{r}\mathrm{cos}\:\theta−\mathrm{4}+{i}\left(\mathrm{4}{r}\mathrm{sin}\:\theta\right) \\ $$$$\mid{A}_{\mathrm{22}} {B}_{\mathrm{11}} \mid=\mathrm{4}\sqrt{\mathrm{1}+{r}\left({r}−\mathrm{2cos}\:\theta\right)} \\ $$$$\frac{\mid{A}_{\mathrm{22}} {B}_{\mathrm{11}} \mid}{{q}}=\frac{\mathrm{4}\sqrt{\mathrm{1}+{r}\left({r}−\mathrm{2cos}\:\theta\right)}}{\:\sqrt{\mathrm{1}+{r}\left({r}−\mathrm{2cos}\:\theta\right)}}\:=\:\mathrm{4} \\ $$$$\Rightarrow\:\:\:{v}=\:\mathrm{4}{q} \\ $$$${similary}\:\:{w}=\:{B}_{\mathrm{22}} {O}_{\mathrm{11}} =\:\mathrm{4}{r} \\ $$$$\Rightarrow\:\:{Sum}\:{of}\:{areas}\:{of}\:{green}\:{squares} \\ $$$$\:=\:\bigtriangleup_{\mathrm{2}} =\:{u}^{\mathrm{2}} +{v}^{\mathrm{2}} +{w}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{16}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)\:=\:\mathrm{16}\bigtriangleup_{\mathrm{0}} \:. \\ $$
Commented by mr W last updated on 30/Nov/19

$${thank}\:{you}\:{sir}!\:{it}'{s}\:{a}\:{nice}\:{solution}. \\ $$
Commented by mr W last updated on 01/Dec/19

$$\Delta_{\mathrm{1}} =\mathrm{3}\Delta_{\mathrm{0}} \\ $$$$\Delta_{\mathrm{2}} =\mathrm{16}\Delta_{\mathrm{0}} \:\:\:\left({p}=\mathrm{4}\right) \\ $$$$\Delta_{\mathrm{3}} =\mathrm{75}\Delta_{\mathrm{0}} \\ $$$$\Delta_{\mathrm{4}} =\mathrm{361}\Delta_{\mathrm{0}} \:\:\:\left({p}=\mathrm{19}\right) \\ $$$$….. \\ $$$$\Delta_{{n}} =?\Delta_{\mathrm{0}} \\ $$
Commented by mr W last updated on 01/Dec/19

Commented by mr W last updated on 01/Dec/19

$${red},\:{green},\:{pink},\:….\:{squares}\:{are}\:{similar}. \\ $$$${blue},\:{yellow},…\:{squares}\:{are}\:{similar}. \\ $$
