Question Number 74776 by chess1 last updated on 30/Nov/19
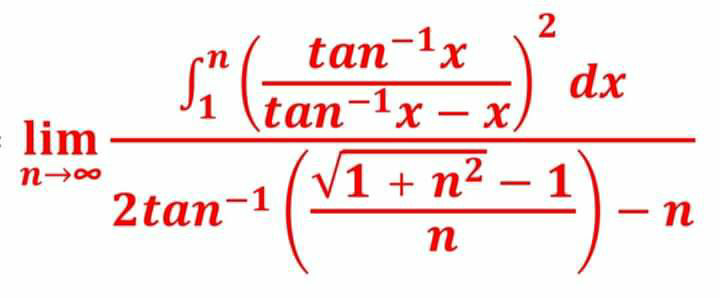
Answered by mind is power last updated on 01/Dec/19
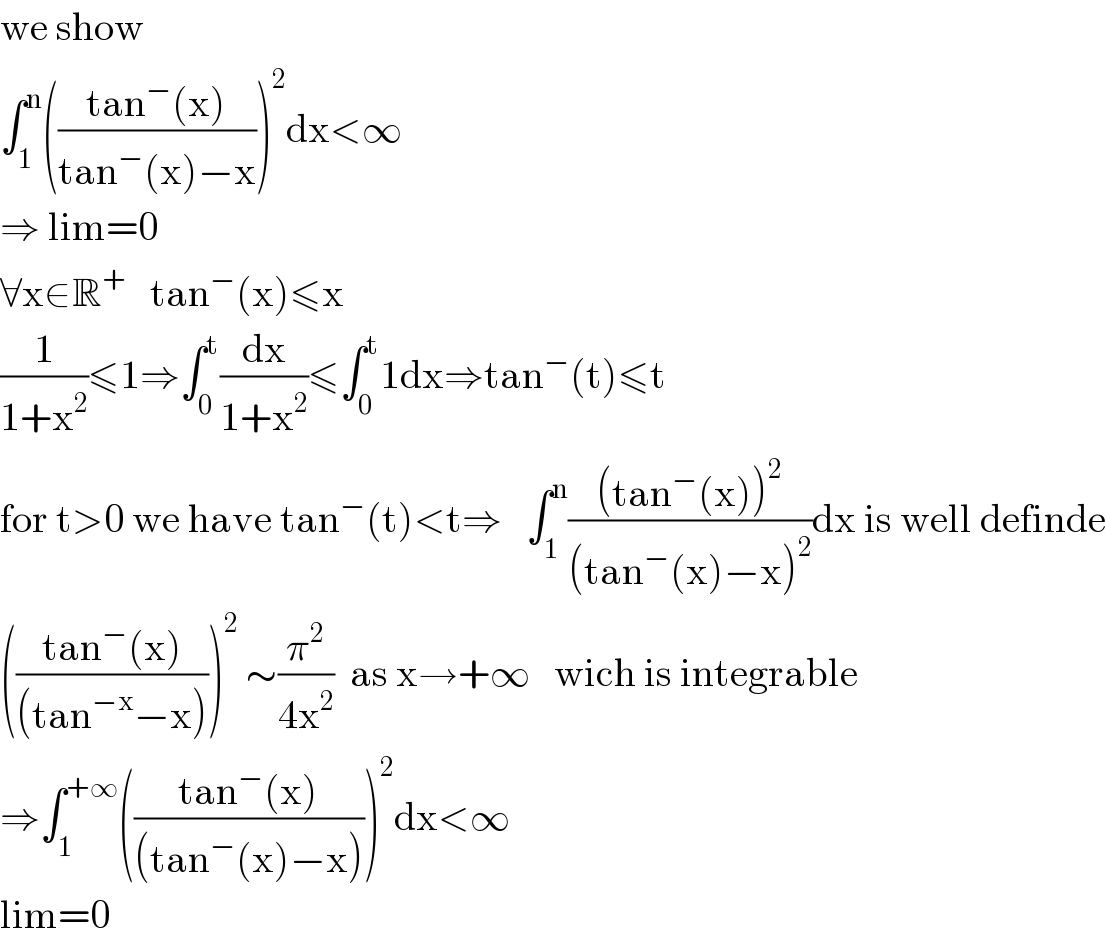
$$\mathrm{we}\:\mathrm{show} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{tan}^{−} \left(\mathrm{x}\right)}{\mathrm{tan}^{−} \left(\mathrm{x}\right)−\mathrm{x}}\right)^{\mathrm{2}} \mathrm{dx}<\infty \\ $$$$\Rightarrow\:\mathrm{lim}=\mathrm{0} \\ $$$$\forall\mathrm{x}\in\mathbb{R}^{+} \:\:\:\mathrm{tan}^{−} \left(\mathrm{x}\right)\leqslant\mathrm{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\leqslant\mathrm{1}\Rightarrow\int_{\mathrm{0}} ^{\mathrm{t}} \frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\leqslant\int_{\mathrm{0}} ^{\mathrm{t}} \mathrm{1dx}\Rightarrow\mathrm{tan}^{−} \left(\mathrm{t}\right)\leqslant\mathrm{t} \\ $$$$\mathrm{for}\:\mathrm{t}>\mathrm{0}\:\mathrm{we}\:\mathrm{have}\:\mathrm{tan}^{−} \left(\mathrm{t}\right)<\mathrm{t}\Rightarrow\:\:\:\int_{\mathrm{1}} ^{\mathrm{n}} \frac{\left(\mathrm{tan}^{−} \left(\mathrm{x}\right)\right)^{\mathrm{2}} }{\left(\mathrm{tan}^{−} \left(\mathrm{x}\right)−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}\:\mathrm{is}\:\mathrm{well}\:\mathrm{definde} \\ $$$$\left(\frac{\mathrm{tan}^{−} \left(\mathrm{x}\right)}{\left(\mathrm{tan}^{−\mathrm{x}} −\mathrm{x}\right)}\right)^{\mathrm{2}} \:\sim\frac{\pi^{\mathrm{2}} }{\mathrm{4x}^{\mathrm{2}} }\:\:\mathrm{as}\:\mathrm{x}\rightarrow+\infty\:\:\:\mathrm{wich}\:\mathrm{is}\:\mathrm{integrable} \\ $$$$\Rightarrow\int_{\mathrm{1}} ^{+\infty} \left(\frac{\mathrm{tan}^{−} \left(\mathrm{x}\right)}{\left(\mathrm{tan}^{−} \left(\mathrm{x}\right)−\mathrm{x}\right)}\right)^{\mathrm{2}} \mathrm{dx}<\infty \\ $$$$\mathrm{lim}=\mathrm{0} \\ $$
Commented by chess1 last updated on 01/Dec/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
