Question Number 74821 by sridhar nayak last updated on 01/Dec/19
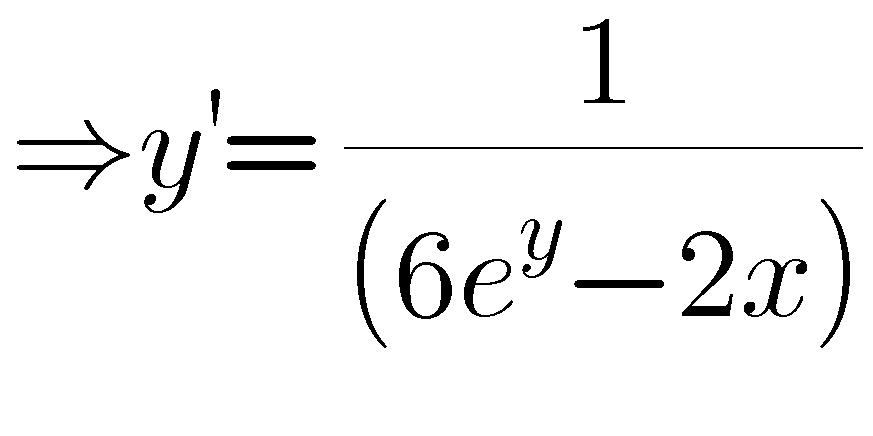
Answered by mind is power last updated on 01/Dec/19
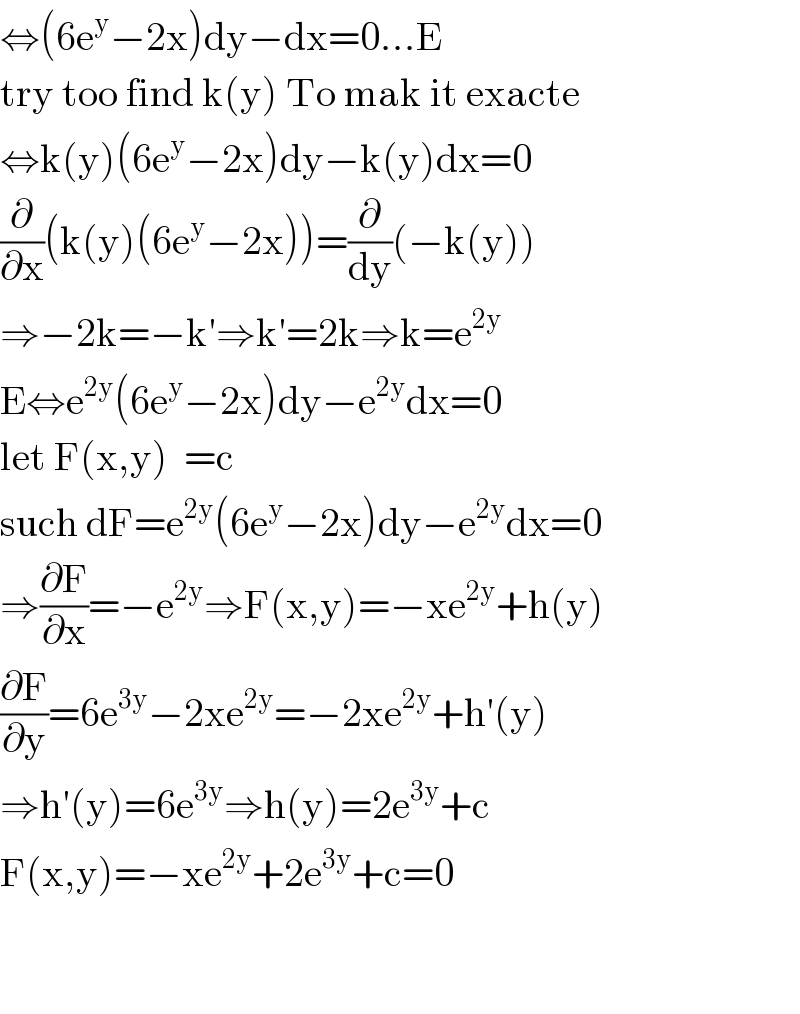
$$\Leftrightarrow\left(\mathrm{6e}^{\mathrm{y}} −\mathrm{2x}\right)\mathrm{dy}−\mathrm{dx}=\mathrm{0}…\mathrm{E} \\ $$$$\mathrm{try}\:\mathrm{too}\:\mathrm{find}\:\mathrm{k}\left(\mathrm{y}\right)\:\mathrm{To}\:\mathrm{mak}\:\mathrm{it}\:\mathrm{exacte} \\ $$$$\Leftrightarrow\mathrm{k}\left(\mathrm{y}\right)\left(\mathrm{6e}^{\mathrm{y}} −\mathrm{2x}\right)\mathrm{dy}−\mathrm{k}\left(\mathrm{y}\right)\mathrm{dx}=\mathrm{0} \\ $$$$\frac{\partial}{\partial\mathrm{x}}\left(\mathrm{k}\left(\mathrm{y}\right)\left(\mathrm{6e}^{\mathrm{y}} −\mathrm{2x}\right)\right)=\frac{\partial}{\mathrm{dy}}\left(−\mathrm{k}\left(\mathrm{y}\right)\right) \\ $$$$\Rightarrow−\mathrm{2k}=−\mathrm{k}'\Rightarrow\mathrm{k}'=\mathrm{2k}\Rightarrow\mathrm{k}=\mathrm{e}^{\mathrm{2y}} \\ $$$$\mathrm{E}\Leftrightarrow\mathrm{e}^{\mathrm{2y}} \left(\mathrm{6e}^{\mathrm{y}} −\mathrm{2x}\right)\mathrm{dy}−\mathrm{e}^{\mathrm{2y}} \mathrm{dx}=\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)\:\:=\mathrm{c} \\ $$$$\mathrm{such}\:\mathrm{dF}=\mathrm{e}^{\mathrm{2y}} \left(\mathrm{6e}^{\mathrm{y}} −\mathrm{2x}\right)\mathrm{dy}−\mathrm{e}^{\mathrm{2y}} \mathrm{dx}=\mathrm{0} \\ $$$$\Rightarrow\frac{\partial\mathrm{F}}{\partial\mathrm{x}}=−\mathrm{e}^{\mathrm{2y}} \Rightarrow\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)=−\mathrm{xe}^{\mathrm{2y}} +\mathrm{h}\left(\mathrm{y}\right) \\ $$$$\frac{\partial\mathrm{F}}{\partial\mathrm{y}}=\mathrm{6e}^{\mathrm{3y}} −\mathrm{2xe}^{\mathrm{2y}} =−\mathrm{2xe}^{\mathrm{2y}} +\mathrm{h}'\left(\mathrm{y}\right) \\ $$$$\Rightarrow\mathrm{h}'\left(\mathrm{y}\right)=\mathrm{6e}^{\mathrm{3y}} \Rightarrow\mathrm{h}\left(\mathrm{y}\right)=\mathrm{2e}^{\mathrm{3y}} +\mathrm{c} \\ $$$$\mathrm{F}\left(\mathrm{x},\mathrm{y}\right)=−\mathrm{xe}^{\mathrm{2y}} +\mathrm{2e}^{\mathrm{3y}} +\mathrm{c}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
